Tré zákonů/zákazů termodynamických
Jan Obdržálek
ZÁKON TERMODYNAMIKY PRVÝ: NEZÍSKÁŠ SYSTÉMU SVÉMU ENERGIE JEN TAK ZBŮHDARMA
Neboť
tak stojí psáno v Knize knih Přírody: Energie-li se systému tvému
zachce, může ji míti; jedině však tehdáž, pakliže jemu dodáš buďsi
teplo, buďsi práci, buďsi práci chemickou (totiž systému toho složení
tak či onak pozměníš).
Jazykem dnešním bychom řekli:
Jestliže se nemění chemické složení systému, potom je přírůstek ΔU vnitřní energie systému roven součtu úhrnného tepla Q a práce W dodaných systému, tedy
ΔU = Q + W
Pokud se chemické složení systému mění, přiřadíme každé z K komponent – neboli složek systému – chemický potenciál µ; může být kladný i záporný podle toho, o kterou látku se jedná a jakou teplotu T a tlak p má: µ = µ (T, p). Přidáme-li j–té komponenty množství Δnj , pak energie systému vzroste o
ΔU = Q + W + µ1Δn1 + µ2Δn2 + ... + µKΔnK
Jak
známo, motor, který by stále dodával energii z ničeho, se nazývá
„perpetuum mobile“ neboli „věčný samohyb“ – přesněji perpetuum mobile
1. druhu. (Neberte tento historický název doslova. Přežívá
v něm aristotelovská představa, že k pohybu je potřebná síla.
Tato představa ale byla newtonovskou mechanikou překonaná. Nejde jen
o to, aby se něco pořád pohybovalo – to umí třeba Brownův pohyb –,
ale aby to přitom dodávalo energii.)
Trošku to ale
upřesníme: za perpetuum mobile byste jistě nepokládali natažený budík,
který jistou dobu klape, ale pak dojde a vy ho musíte znovu
natáhnout. Perpetuum mobile by se muselo umět „natáhnout samo“, tedy
z jistého výchozího stavu projít řadu stavů jiných a nakonec
se zase vrátit do původního stavu, a během tohoto cyklického děje
by muselo vyrobit a dodat do okolí víc energie, než by ji ze svého
okolí přijalo. Jaké štěstí, že to nejde! Nejsme-li zrovna
v chemické továrně, tak prakticky všechna mechanická práce, kterou
na zemi vykonáme, se „promění v teplo“, tj. koneckonců zahřeje
naší planetu. Už vidím, jak by si lidi udělali tolik a tak
výkonných perpetuí, že by si přehřáli svou rodnou planetu ještě mnohem
rychleji, než si ji mrháním v minulosti uložených energií
přehřívají dnes.
Dodejme ještě, že vnitřní energie U
je stavová veličina. To znamená, že má rozumný smysl pro systém, který
je v určitém stavu (horká voda v hrnci, taška plná dynamitu).
Pro něj lze říct, jakou má energii neboli jaká energie je v něm
uložena. Naproti tomu teplo Q, práce W, chemická práce Wch
jsou veličiny dějové, tedy vázané na konkrétní děj: teplo dodané při
zahřívání, práce vykonaná při smrštění zahřáté gumy, energie uvolněná
chemickou reakcí. Můžeme tedy třeba říct, že jsme použili dvou
watthodin (2 Wh = 7 200 Ws = 7,2kJ) chemické práce hořícího svítiplynu
a dodali z nich do vody třeba jednu watthodinu tepla.
v teplé vodě však není navíc 1 Wh tepla, ale 1 Wh energie.
z hrnku teplé vody už nikdy nepoznáte, zda a jaká část
energie se do vody dostala přenosem tepla, nebo konáním práce, nebo
chemickou prácí.
Je to asi jako u peněz ve spořitelně. Výše vašeho konta (finanční stav)
je stavová veličina. Výpis stavu dnešního dne vám řekne, že tam máte 12
000 Kč, ale nemůže říct, jaká část z nich připlula dějem „převod
z jiného konta“, dějem „úrok“ nebo dějem „vklad v hotovosti“.
Tyto tři veličiny jsou dějové, a sledujete-li,
co se s vaším kontem děje, pak je navzájem snadno rozlišíte. Pokud
ale máte k dispozici nikoli popis celého děje, ale jen jeho výsledek – okamžitý stav, pak má smysl mluvit jen o stavové
veličině (výše konta, energie). Nelze z ní však poznat, zda
a kolik vám přibylo konkrétním dějem (úrokem u konta, zahřátím u
vody).
ZÁKON TERMODYNAMIKY DRUHÝ: NEPROMĚNÍŠ TEPLA VŠEHO ZA PRÁCI DLE LIBOSTI SVÉ.
ANEBO TAKTÉŽ, VE CHLADU ODPOČÍVAJE, TOLIKO PROCHLADNOUTI MŮŽEŠ
Neboť
tak stojí psáno v Knize knih Přírody: Teplo nelze nikterak pořád
do kruhu z jediné toliko lázně čerpati a v práci měniti.
Aneboli jináče pověděno: Teplo z teplé věci na chladnější samo
přeleze, nikdáž však naopak – leda by ho k tomu prací nutili.
Mluvíme
o tepelných strojích. Může to být motor, kterému dodáváme teplo
a odebíráme z něj práci. Pokud naopak stroji práci dodáváme
a přečerpáváme tím teplo (i s jistým přídavkem), je to buď
chladnička (zajímá-li nás ta část, odkud teplo čerpáme), anebo tepelné
čerpadlo (zajímá-li nás naopak ta část, kterou vyhříváme).
První
znění (Thomson, 1851): Tepelný motor musí mít alespoň dvě lázně různých
teplot. z teplejší lázně odebírá teplo, do chladnější toto teplo
dodává (zmenšené o ekvivalent vykonané práce).
Druhé
znění (Clausius, 1850) zakazuje samovolný přechod tepla z předmětu
studenějšího na předmět teplejší. Opačným směrem – z teplého na
studené – může teplo přecházet samovolně, ale ochladit studený předmět
ještě víc – to stojí energii (která se pak předá nějakému teplejšímu
tělesu v okolí).
Tak tady je toho na vysvětlování hodně; musíme např. ukázat, že obě formulace jsou si ekvivalentní.
Napřed si ale ukážeme názorné schéma
pro rozbor cyklických termodynamických strojů. Protože budeme zřejmě
mít nikoli jedinou, ale dvě tepelné lázně (něco jako přívod
a odvod tepla), nakreslíme si je jako obdélníčky – teplou lázeň L2 nahoru, studenou L1
dolů – a mezi ně náš stroj jako kroužek. Šipky budou znamenat směr
přenosu energie. Bude u nich číslo udávající, kolik energie se během
cyklu ve směru šipky přeneslo: jde-li ze stroje ven, mají symboly Q, W
čárku, jde-li dovnitř, nemají ji. Čárku píšeme či nepíšeme tak, abychom
ve schématech zapisovali jen kladná čísla. Zákon zachování energie
(1. zákon termodynamiky) říká, že po návratu do výchozího stavu se
vnitřní energie U stroje nezměnila; musí tedy platit (tato rovnice je vždy bez čárek)!
W+Q1+Q2=0.
A teď si vzpomeňte, že Q = – Q a W ’ = – W, a podle toho dosaďte správné hodnoty.
Jsou-li tyto stroje vratné, pak je lze „spustit pozpátku“: na našem schématu pak jen obrátíme směry všech šipek a změníme očárkování u Q, W.
Co nám tedy říká 2. zákon termodynamiky? Zapovídá nám následující stroje:
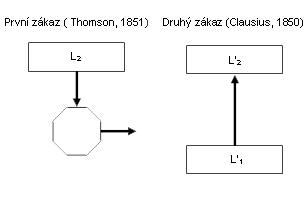
JEDNO KAŽDÉ Z OBOJÍHO SE ZAPOVÍDÁ
První
znění tedy zakazuje 100% proměnu tepla v práci (tzv. perpetuum
mobile 2. druhu). Všimněte si, že toto perpetuum mobile nenarušuje
zákon zachování energie. Bylo by to krásné, byl by to ekologický zdroj
energie k pohledání. Ale v přírodě není. a nikdy
nebude.
Druhé znění zakazuje, aby se teplo (bez
dodání práce) přenášelo z chladnějšího tělesa na teplejší. Obě
znění jsou celkem snadno pochopitelná i přijatelná. Ale jak
z toho dostat něco konstruktivního? a jak ukázat, že
z jednoho plyne druhé?
Především se ujistíme, že něco
jako tepelný stroj existuje. Každý, kdo si ruční hustilkou pumpoval
kolo, ví dobře, že se časem hustilka značně ohřeje. Ohřívá se od
stlačovaného vzduchu uvnitř (celkem pomalu, protože má přece jen oproti
té trošce vzduchu uvnitř i vzduchu v pneumatice podstatně
větší tepelnou kapacitu).
Kdybychom zvolna
stlačovali vzduch v ucpané pumpičce na poloviční objem – tak
pomalu, aby se stlačovaný vzduch stačil ochladit od pumpičky okolním
vzduchem a měl pořád pokojovou teplotu – pak by na konci
stlačování měl dvakrát větší tlak, teplotu opět pokojovou
a vnitřní energii proto kupodivu prakticky stejnou, jako když byl
nestlačený. To, co jsme do něj dodali stlačováním (konáním práce), zase
odebral okolní vzduch, když nám naši pumpičku ochlazoval (odebíráním
tepla).
Kdybychom však dokázali vzduch tepelně odizolovat,
anebo jednodušeji stlačili vzduch na poloviční objem tak rychle, aby se
žádné teplo s okolím (ani s pumpičkou) nestačilo vyměnit –
tzv. adiabatický děj – vzrostl by tlak vzduchu asi 2,6x a jeho
teplota by z pokojové vzrostla asi o 90 °C. Díky vyššímu
tlaku vzduchu bychom přitom museli vykonat práci podstatně větší,
a o ni by i vzrostla vnitřní energie vzduchu. Naopak: pokud
se stlačený vzduch rozpíná, může konat práci; ta bude menší, jestliže
ponecháme rozpínaný vzduch chladnout, než když ho budeme udržovat
(dodáváním tepla) při stejné teplotě.
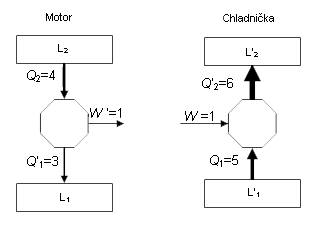
Chceme-li tedy postavit motor co nejnázorněji, vyjdeme ze stlačeného horkého vzduchu, necháme ho rozpínat a nejprve udržujeme horký (dodáváme teplo Q2), pak zdroj tepla odstavíme, takže dalším rozpínáním teplota vzduchu klesne. Dokud se vzduch rozpínal, dodával nám práci W ’2. Část této práce nyní použijeme na návrat zpět: studený plyn stlačujeme a chladíme ho, aby se nezahříval (odebíráme teplo Q ’1), poté už jen stlačujeme, aby se vyhřál na původní vysokou teplotu. Ke stlačování spotřebujeme část W1
získané práce, ta je ovšem menší než práce získaná, protože jsme
stlačovali plyn nižší teploty a tedy i tlaku, než když jsme
plyn rozpínali. Tento motor tedy vyrobí W’2 – W1 práce z Q2 tepla (a Q ’1 tepla se předá do chladnějšího okolí).
Chceme-li postavit chladničku,
necháme právě popsaný motor běžet pozpátku; „horký“ bude vzduch
v místnosti a „studený“ bude vnitřek chladničky.
Takže zpět k výkladu: dokážeme nejprve ekvivalenci obou formulací 2. zákona termodynamiky:
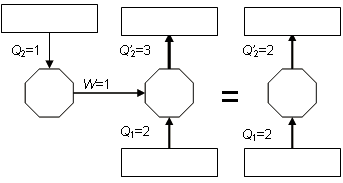
Zapojíme-li
tedy na perpetuum mobile 2. druhu chladničku, budeme nakonec bez
dodávání práce přenášet teplo ze studeného prostředí do teplého –
a to, bohužel, nejde podle druhé formulace.
Pokud
bychom naopak uměli bez práce převádět teplo z chladné lázně do
teplejší (což také neodporuje zákonu zachování energie!), stačilo by
pak mezi ně napojit obvyklý tepelný motor (dostali byste předchozí
obrázek „pozpátku“ – umíte si to sami nakreslit?), a měli bychom
perpetuum mobile 2. druhu. Což zase nejde, tentokrát podle první
formulace.
Tím máme ekvivalenci obou formulací úspěšně za sebou. a jak dál se zavedením teploty?
Nejdříve malé překvapení: účinnost všech vratných motorů
pracujících mezi danými dvěma lázněmi je přesně stejná, nezávislá na
konstrukci stroje! Jak je to možné? Podívejte se na první obrázek
s motorem a chladničkou. Kdyby teploty lázní na obou
obrázcích byly stejné a chladnička pracovala „obráceně“, jako
motor, pak by měla menší účinnost (1/6) než motor vlevo (1/4). To je
výborné – jejich propojením bych získal stroj, který by koneckonců za
jeden cykl převedl 2 díly tepla ze studené do teplé lázně – ale to
nedovoluje druhé znění 2. zákona termodynamiky. Pokud tedy oba
stroje jsou vratné a pracují tak, jak, je uvedeno, pak mají různě
teplé pracovní lázně!
Účinnost motoru je rovna
podílu co dostanu/co zaplatím (obojí kladné – podle toho budou čárky).
V tomto případě platím teplo Q2, dostávám práci W’, a účinnost je tedy (pozor na čárky u proměnných!)
η = W’ / Q2 = (Q2 – Q’1) / Q2
η = 1 – (Q’1 / Q2 )< 1 .
Protože je dána jen teplotami lázní, lze zřejmě také naopak zavést teplotu
(termodynamickou) podle této univerzální účinnosti: teplota lázně bude
prostě úměrná množství vyměněného tepla. Kdyby na našem obrázku měly
obě „studené lázně“ stejnou teplotu T1 = T’1 = 300 K, pak T2 = 400 K a T’2 = 360 K, aby byly zachovány poměry teplot a vyměněných tepel.
Aby nenastala vzpoura praktiků a techniků na celé zeměkouli, bylo pro zavedení termodynamické teploty potřeba
- rozumně zvolit dobře definovatelnou a reprodukovatelnou referenční teplotu,
- přiřadit jí takovou hodnotu v kelvinech, aby se kelvin co možná nelišil od stupně Celsia.
Což
se prozatím podařilo tím, že za referenční teplotu se vzal trojný bod
vody – tedy ta teplota, při níž může být spolu v rovnováze voda
plynná (pára), kapalná i pevná (led), a protože mu
v dosavadní Celsiově stupnici odpovídá teplota 0,01 °C, tak
mu byla přiřazena teplota právě 273,16 K. Tím „bod mrazu“ 0 °C
odpovídá 273,15 K, přírůstek 1 °C = 1 K a bod varu vody
zůstal zhruba o 100 °C výš než bod mrazu. Po bitvě je každý
generálem: kdybychom to tehdy určovali my se současnou přesností měření
teploty, zvolili bychom 273,22, a vyšlo by to lépe. Ale za opravu
to nestojí, protože bod varu vody (nyní za standardního tlaku 99,974
°C) není zas až tak důležitý, abychom trvali na přesných
100 °C. Větší problém je, že i ta nejčistší,
„nejpředestilovanější a iontově nejvyměněnější“ voda může mít
ještě různé izotopové složení, protože máme 2 typy vodíku (1H, 2D) a tři typy kyslíku (16O, 17O, 18O).
Takže se pracuje na nové definici teploty, dané tak, aby si vhodná
univerzální konstanta (zde to bude Boltzmannova konstanta k), zachovala dosavadní hodnotu.
Tím
bychom měli slíbené za sebou; ale my ještě přidáme pilnému čtenáři dva
pamlsky: praktikům připomeneme a přiblížíme tepelná čerpadla,
teoretikům zavedeme entropii – míru chaosu.
Tepelné čerpadlo
Chladničku
jistě znáte: uvnitř má mrazák s –20 °C, venku vzadu žebroví,
které se hodně hřeje, a má ještě elektromotor. Ten stlačuje plyn,
který se tím ohřívá, stlačený v žebroví se okolním vzduchem
ochlazuje a pak se zpět uvnitř, v mrazáku, rozpíná; přitom se
naopak ochlazuje hodně pod svou původní teplotu. Její chladicí faktor
(rozlišujme „i – í“: „chladicí“ = týkající se chlazení, „chladící“ =
ten, co právě teď chladí) je opět známý podíl (co dostanu) / (co
zaplatím). v tomto případě platím dodanou práci W, dostávám „mrazáku odebrané teplo“ Q1, a účinnost je tedy
η = Q1 / W = Q1 /(Q’2 – Q1).
Chladicí faktor může být i větší, i menší než jednička.
Žebroví
za chladničkou je vždy dosti teplé: musí vyzářit jednak všechnu dodanou
elektrickou energii, jednak i to množství tepla, které musíme
stále odčerpávat z mrazáku (kvůli nedokonalé izolaci), aby zůstal
tak chladný, jak my si přejeme.
Tepelné čerpadlo
z chladničky dostaneme tak, že chladničku postavíme
v místnosti k oknu, žebrovím k nám, a mrazák
vytáhneme až před dům, do potůčku tekoucího pod okny. Ten má i
v zimě teplotu kolem 4 °C. „Chladnička“ – tepelné čerpadlo
nyní tedy chladí potůček. Odebírá od něj teplo a převádí ho spolu
s dodávanou elektrickou energií přes žebroví do našeho pokoje.
Topný faktor tepelného čerpadla je i zde roven podílu (co dostanu)
/ (co zaplatím). v tomto případě platím práci W, dostávám teplo Q’2, a topný faktor je tedy k našemu potěšení vždy větší než 1 (uvažte proč!)
η = Q’2 / W = Q’2 / (Q’2 – Q1) = 1 + Q1 / (Q’2 – Q1)
Entropie
Převádíme-li za teploty T vratným způsobem teplo Q, pak můžeme zavést veličinu S = Q / T. Dříve se jí říkalo „redukované teplo“, nyní zavádíme entropii. Je to veličina extenzivní, entropie celého systému tedy je rovna součtu entropií jeho částí. (Exenzivní je taky třeba energie, objem, počet částic. U
veličin intenzivních, jako je třeba tlak a teplota, je tomu
v rovnováze jinak: např. tlak v celém objemu plynu je stejný
jako tlak v každé jeho části, není to „součet dílčích tlaků“.)
Entropie souvisí s pravděpodobností a tím i s chaosem:
Samovolný vývoj směřuje vždy k více pravděpodobnému a tedy
k „chaotičtějšímu“ stavu. Entropii můžeme zavést i hodně
daleko od fyziky, totiž v informatice, a to stejným
principem: entropie S je úměrná logaritmu pravděpodobnosti w, tedy
S = k ln w,
protože
pro systém složený ze dvou nezávislých částí se pravděpodobnosti jeho
částí násobí, zatímco jejich entropie se sčítají. Pravděpodobnost w
stavu je přitom úměrná počtu různých mikrostavů (individuálních
rozložení jednotlivých molekul tvořících systém), které se nám jeví
jako stejný makroskopický stav.
Při vratných dějích
se entropie nemění. Nevratné děje probíhají samovolně vždy tak, že
entropie celku roste. (Entropie části může klesat, pokud dostatečně
roste entropie nějaké jiné části systému.)
TŘETÍ ZÁKON TERMODYNAMIKY: NEDOJDEŠ NIKDÁŽ POŘÁDKU ÚPLNÉHO, LEČ JEN V POTU TVÁŘE SE TOMUTO BLÍŽITI SMÍŠ
Nebo
tak stojí psáno v Knize knih Přírody: Každý pak systém, kterýž by
sis kde vymyslil, jedině jeden jediný ze stavů všech svých takový má,
žeť energií jsa nejchudší, však pořádkem nejbohatší jest, kterýžto stav
pak teplotě nuly absolutní odpovídá, entropii pak taktéž nulovou maje.
Rozuměj:
„Snižovat
teplotu“ znamená „zmenšovat kinetickou energii“ chaotického pohybu
částic systému, a tím také zvyšovat uspořádanost systému. Každý
reálný systém má jediný stav s nejnižší energií; tomu přísluší
nejnižší entropie (neuspořádanost) a nejnižší teplota; obě lze
položit rovny nule jako základ stupnice. Tento stav je nedosažitelný
konečným počtem kroků; můžeme se mu jen blížit. Také účinnost všech
chladicích postupů se snižuje tak, jak se tomuto stavu („absolutní
nule“) blížíme.
Tady je to celkem srozumitelné. (Pravda,
uklízejíce pokoj svůj pod dozorem rodičů svých, pozorujeme to
a cítíme to jako křivdu od přírody, ale co se dá dělat.)
Makrostav systému v „naprostém pořádku“,
bez jakékoli energie navíc, je realizován pouze jedním jediným
mikrostavem, v němž je každá molekula systému „na svém místě“ (ve
ztuhlém krystalu látky) a v klidu. Protože je tento mikrostav jediný, je pravděpodobnost jeho výskytu v tomto makrostavu „naprostého pořádku“ dána jistotou – je rovna jedné. Proto je entropie tohoto makrostavu rovna nule, log 1 = 0. Energie je vskutku nejmenší a můžeme ji tedy také položit rovnu nule. Můžete se ptát, jak to je s Einsteinovou energií E = m c2.
Tu zde neuvažujeme proto, že ji nemůžeme nijak od systému odebrat.
Pokud ji tedy bude mít systém stejnou vždy a všude, pak se
neprojeví v žádných rozdílech energií udávajících teplo, práci,
anebo chemickou práci, a nemusíme ji uvažovat vůbec.
Tento
zákon jaksi „završuje“ celou trojici. Druhý zákon umožnil zavést
objektivní nezávislou teplotu, a to i s její „počáteční
hodnotou“; naproti tomu u entropie (např. u redukovaného tepla) šlo
vždy jen o děj, kterým se entropie zvětšovala nebo zmenšovala.
„Počáteční hodnota“ však chyběla. Tu tedy nyní stanovuje třetí zákon
termodynamiky.
Teoretická nedosažitelnost onoho
jediného stavu s minimální energií souhlasí s jeho praktickou
nedosažitelností. Připomeňme např. náš dosavadní systém chlazení (s
rozpínáním plynu tak, aby přitom konal práci a nedostával teplo).
Snížení teploty je úměrné příslušnému snížení energie (vykonané práci),
a činitel úměrnosti je měrné teplo plynu. To se ale u skutečných
látek při velice nízkých teplotách také blíží nule, takže proces
ochlazování je čím dále, tím méně účinný (nehledě na to, že každý
skutečný plyn dostatečným ochlazením zkapalní až ztuhne).
Představíme-li
si systém s nenulovou teplotou jako předměty v kočáře
kodrcajícím přes hrubou kamennou dlažbu, pak „ochladit“ znamená
vytvořit v kočáře prostředí, kde by věci byly ve větším klidu. Ve
Vesmíru je velmi mnoho hvězd, které jsou uvnitř tak horké, jak na Zemi
zatím neumíme nic zahřát (a snažíme se o to, umožnilo by nám to
termojadernou fúzi jako zdroj energie!). Naproti tomu mezihvězdný
prostor rozpínáním Vesmíru už jen chladne a v současnosti má jen
pouhých 2,7 K. Protože podle 2. zákona termodynamiky se
nemůže předmět bez dodávání práce ochladit pod teplotu svého okolí,
můžeme být plným právem pyšní na to, že u nás na Zemi, v každé
laboratoři nízkých teplot, máme k dispozici něco, co není nikde
jinde ve Vesmíru (tedy nikde tam, kde zelení mužíčkové nemají své
experimentální laboratoře nízkých teplot).
Doporučená literatura k tématu:
Standardní
učebnice termodynamiky nebo fyzikální chemie z libovolného
nakladatelství odborné či pedagogické (nikoli alternativní!)
literatury.
Na webu, jako obvykle,. Wikipedie: http://cs.wikipedia.org/wiki/Termodynamický_zákon
(napsat s diakritikou!)
Pozn.
autora: Zatímco perpetuum mobile 1. druhu už vynálezce omrzelo,
2. zákon termodynamiky nachází stále své „přemožitele“. Pokud se
totiž místo skutečného pokusu jen citují jiní „přemožitelé“, využívá se
„éterická energie“ apod., pak lze všelicos, viz např. týž článek na
třech různých adresách
http://www.upramene.cz/energie/view.php?cisloclanku=2006112301
http://www.atlantislabs.sk/peter-lindemann-termodynamika-a-volna-energia?page=2
http://www.mwm.cz/clanek1.php?id=120&pjmeno=&kredit=&p1=
Doc. Jan Obdržálek
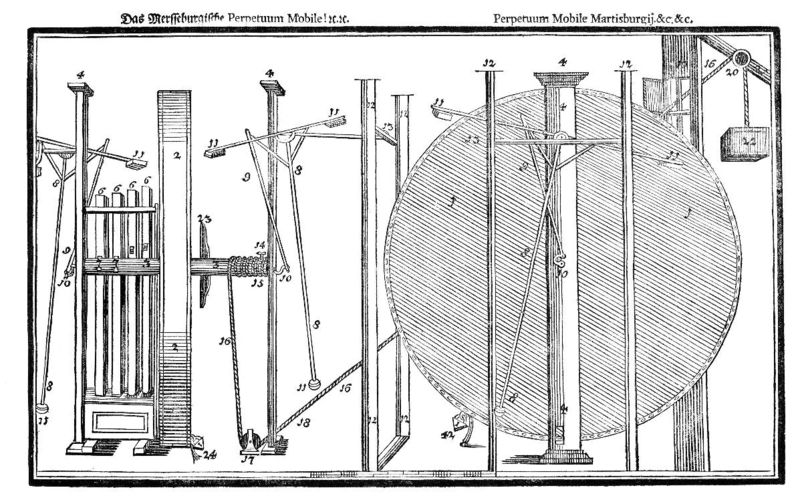
Perpetuum
mobile je utopie. Příklad jednoho z nich - Perpetuum mobile Johanna
Ernsta Eliase Besslera z roku 1719 (a my bychom upřesnili: perpetuum
mobile 1. druhu)
ZÁKON TERMODYNAMIKY PRVÝ: NEZÍSKÁŠ SYSTÉMU SVÉMU ENERGIE JEN TAK ZBŮHDARMA
Neboť tak stojí psáno v Knize knih Přírody: Energie-li se systému tvému zachce, může ji míti; jedině však tehdáž, pakliže jemu dodáš buďsi teplo, buďsi práci, buďsi práci chemickou (totiž systému toho složení tak či onak pozměníš).
Neboť tak stojí psáno v Knize knih Přírody: Energie-li se systému tvému zachce, může ji míti; jedině však tehdáž, pakliže jemu dodáš buďsi teplo, buďsi práci, buďsi práci chemickou (totiž systému toho složení tak či onak pozměníš).
Jazykem dnešním bychom řekli:
Jestliže se nemění chemické složení systému, potom je přírůstek ΔU vnitřní energie systému roven součtu úhrnného tepla Q a práce W dodaných systému, tedy
ΔU = Q + W
Pokud se chemické složení systému mění, přiřadíme každé z K komponent – neboli složek systému – chemický potenciál µ; může být kladný i záporný podle toho, o kterou látku se jedná a jakou teplotu T a tlak p má: µ = µ (T, p). Přidáme-li j–té komponenty množství Δnj , pak energie systému vzroste o
ΔU = Q + W + µ1Δn1 + µ2Δn2 + ... + µKΔnK
ΔU = Q + W
Pokud se chemické složení systému mění, přiřadíme každé z K komponent – neboli složek systému – chemický potenciál µ; může být kladný i záporný podle toho, o kterou látku se jedná a jakou teplotu T a tlak p má: µ = µ (T, p). Přidáme-li j–té komponenty množství Δnj , pak energie systému vzroste o
ΔU = Q + W + µ1Δn1 + µ2Δn2 + ... + µKΔnK
Jak známo, motor, který by stále dodával energii z ničeho, se nazývá „perpetuum mobile“ neboli „věčný samohyb“ – přesněji perpetuum mobile 1. druhu. (Neberte tento historický název doslova. Přežívá v něm aristotelovská představa, že k pohybu je potřebná síla. Tato představa ale byla newtonovskou mechanikou překonaná. Nejde jen o to, aby se něco pořád pohybovalo – to umí třeba Brownův pohyb –, ale aby to přitom dodávalo energii.)
Trošku to ale upřesníme: za perpetuum mobile byste jistě nepokládali natažený budík, který jistou dobu klape, ale pak dojde a vy ho musíte znovu natáhnout. Perpetuum mobile by se muselo umět „natáhnout samo“, tedy z jistého výchozího stavu projít řadu stavů jiných a nakonec se zase vrátit do původního stavu, a během tohoto cyklického děje by muselo vyrobit a dodat do okolí víc energie, než by ji ze svého okolí přijalo. Jaké štěstí, že to nejde! Nejsme-li zrovna v chemické továrně, tak prakticky všechna mechanická práce, kterou na zemi vykonáme, se „promění v teplo“, tj. koneckonců zahřeje naší planetu. Už vidím, jak by si lidi udělali tolik a tak výkonných perpetuí, že by si přehřáli svou rodnou planetu ještě mnohem rychleji, než si ji mrháním v minulosti uložených energií přehřívají dnes.
Dodejme ještě, že vnitřní energie U je stavová veličina. To znamená, že má rozumný smysl pro systém, který je v určitém stavu (horká voda v hrnci, taška plná dynamitu). Pro něj lze říct, jakou má energii neboli jaká energie je v něm uložena. Naproti tomu teplo Q, práce W, chemická práce Wch jsou veličiny dějové, tedy vázané na konkrétní děj: teplo dodané při zahřívání, práce vykonaná při smrštění zahřáté gumy, energie uvolněná chemickou reakcí. Můžeme tedy třeba říct, že jsme použili dvou watthodin (2 Wh = 7 200 Ws = 7,2kJ) chemické práce hořícího svítiplynu a dodali z nich do vody třeba jednu watthodinu tepla. v teplé vodě však není navíc 1 Wh tepla, ale 1 Wh energie. z hrnku teplé vody už nikdy nepoznáte, zda a jaká část energie se do vody dostala přenosem tepla, nebo konáním práce, nebo chemickou prácí.
Je to asi jako u peněz ve spořitelně. Výše vašeho konta (finanční stav) je stavová veličina. Výpis stavu dnešního dne vám řekne, že tam máte 12 000 Kč, ale nemůže říct, jaká část z nich připlula dějem „převod z jiného konta“, dějem „úrok“ nebo dějem „vklad v hotovosti“. Tyto tři veličiny jsou dějové, a sledujete-li, co se s vaším kontem děje, pak je navzájem snadno rozlišíte. Pokud ale máte k dispozici nikoli popis celého děje, ale jen jeho výsledek – okamžitý stav, pak má smysl mluvit jen o stavové veličině (výše konta, energie). Nelze z ní však poznat, zda a kolik vám přibylo konkrétním dějem (úrokem u konta, zahřátím u vody).
ZÁKON TERMODYNAMIKY DRUHÝ: NEPROMĚNÍŠ TEPLA VŠEHO ZA PRÁCI DLE LIBOSTI SVÉ.
ANEBO TAKTÉŽ, VE CHLADU ODPOČÍVAJE, TOLIKO PROCHLADNOUTI MŮŽEŠ
Neboť tak stojí psáno v Knize knih Přírody: Teplo nelze nikterak pořád do kruhu z jediné toliko lázně čerpati a v práci měniti. Aneboli jináče pověděno: Teplo z teplé věci na chladnější samo přeleze, nikdáž však naopak – leda by ho k tomu prací nutili.
Mluvíme
o tepelných strojích. Může to být motor, kterému dodáváme teplo
a odebíráme z něj práci. Pokud naopak stroji práci dodáváme
a přečerpáváme tím teplo (i s jistým přídavkem), je to buď
chladnička (zajímá-li nás ta část, odkud teplo čerpáme), anebo tepelné
čerpadlo (zajímá-li nás naopak ta část, kterou vyhříváme). Neboť tak stojí psáno v Knize knih Přírody: Teplo nelze nikterak pořád do kruhu z jediné toliko lázně čerpati a v práci měniti. Aneboli jináče pověděno: Teplo z teplé věci na chladnější samo přeleze, nikdáž však naopak – leda by ho k tomu prací nutili.
První
znění (Thomson, 1851): Tepelný motor musí mít alespoň dvě lázně různých
teplot. z teplejší lázně odebírá teplo, do chladnější toto teplo
dodává (zmenšené o ekvivalent vykonané práce).
Druhé znění (Clausius, 1850) zakazuje samovolný přechod tepla z předmětu studenějšího na předmět teplejší. Opačným směrem – z teplého na studené – může teplo přecházet samovolně, ale ochladit studený předmět ještě víc – to stojí energii (která se pak předá nějakému teplejšímu tělesu v okolí).
Druhé znění (Clausius, 1850) zakazuje samovolný přechod tepla z předmětu studenějšího na předmět teplejší. Opačným směrem – z teplého na studené – může teplo přecházet samovolně, ale ochladit studený předmět ještě víc – to stojí energii (která se pak předá nějakému teplejšímu tělesu v okolí).
Tak tady je toho na vysvětlování hodně; musíme např. ukázat, že obě formulace jsou si ekvivalentní.
Napřed si ale ukážeme názorné schéma pro rozbor cyklických termodynamických strojů. Protože budeme zřejmě mít nikoli jedinou, ale dvě tepelné lázně (něco jako přívod a odvod tepla), nakreslíme si je jako obdélníčky – teplou lázeň L2 nahoru, studenou L1 dolů – a mezi ně náš stroj jako kroužek. Šipky budou znamenat směr přenosu energie. Bude u nich číslo udávající, kolik energie se během cyklu ve směru šipky přeneslo: jde-li ze stroje ven, mají symboly Q, W čárku, jde-li dovnitř, nemají ji. Čárku píšeme či nepíšeme tak, abychom ve schématech zapisovali jen kladná čísla. Zákon zachování energie (1. zákon termodynamiky) říká, že po návratu do výchozího stavu se vnitřní energie U stroje nezměnila; musí tedy platit (tato rovnice je vždy bez čárek)!
A teď si vzpomeňte, že Q = – Q a W ’ = – W, a podle toho dosaďte správné hodnoty.

Jsou-li tyto stroje vratné, pak je lze „spustit pozpátku“: na našem schématu pak jen obrátíme směry všech šipek a změníme očárkování u Q, W.
Co nám tedy říká 2. zákon termodynamiky? Zapovídá nám následující stroje:

JEDNO KAŽDÉ Z OBOJÍHO SE ZAPOVÍDÁ
První znění tedy zakazuje 100% proměnu tepla v práci (tzv. perpetuum mobile 2. druhu). Všimněte si, že toto perpetuum mobile nenarušuje zákon zachování energie. Bylo by to krásné, byl by to ekologický zdroj energie k pohledání. Ale v přírodě není. a nikdy nebude.
Druhé znění zakazuje, aby se teplo (bez dodání práce) přenášelo z chladnějšího tělesa na teplejší. Obě znění jsou celkem snadno pochopitelná i přijatelná. Ale jak z toho dostat něco konstruktivního? a jak ukázat, že z jednoho plyne druhé?
Především se ujistíme, že něco jako tepelný stroj existuje. Každý, kdo si ruční hustilkou pumpoval kolo, ví dobře, že se časem hustilka značně ohřeje. Ohřívá se od stlačovaného vzduchu uvnitř (celkem pomalu, protože má přece jen oproti té trošce vzduchu uvnitř i vzduchu v pneumatice podstatně větší tepelnou kapacitu).
Kdybychom zvolna stlačovali vzduch v ucpané pumpičce na poloviční objem – tak pomalu, aby se stlačovaný vzduch stačil ochladit od pumpičky okolním vzduchem a měl pořád pokojovou teplotu – pak by na konci stlačování měl dvakrát větší tlak, teplotu opět pokojovou a vnitřní energii proto kupodivu prakticky stejnou, jako když byl nestlačený. To, co jsme do něj dodali stlačováním (konáním práce), zase odebral okolní vzduch, když nám naši pumpičku ochlazoval (odebíráním tepla).
Kdybychom však dokázali vzduch tepelně odizolovat, anebo jednodušeji stlačili vzduch na poloviční objem tak rychle, aby se žádné teplo s okolím (ani s pumpičkou) nestačilo vyměnit – tzv. adiabatický děj – vzrostl by tlak vzduchu asi 2,6x a jeho teplota by z pokojové vzrostla asi o 90 °C. Díky vyššímu tlaku vzduchu bychom přitom museli vykonat práci podstatně větší, a o ni by i vzrostla vnitřní energie vzduchu. Naopak: pokud se stlačený vzduch rozpíná, může konat práci; ta bude menší, jestliže ponecháme rozpínaný vzduch chladnout, než když ho budeme udržovat (dodáváním tepla) při stejné teplotě.
Chceme-li tedy postavit motor co nejnázorněji, vyjdeme ze stlačeného horkého vzduchu, necháme ho rozpínat a nejprve udržujeme horký (dodáváme teplo Q2), pak zdroj tepla odstavíme, takže dalším rozpínáním teplota vzduchu klesne. Dokud se vzduch rozpínal, dodával nám práci W ’2. Část této práce nyní použijeme na návrat zpět: studený plyn stlačujeme a chladíme ho, aby se nezahříval (odebíráme teplo Q ’1), poté už jen stlačujeme, aby se vyhřál na původní vysokou teplotu. Ke stlačování spotřebujeme část W1 získané práce, ta je ovšem menší než práce získaná, protože jsme stlačovali plyn nižší teploty a tedy i tlaku, než když jsme plyn rozpínali. Tento motor tedy vyrobí W’2 – W1 práce z Q2 tepla (a Q ’1 tepla se předá do chladnějšího okolí).
Chceme-li postavit chladničku, necháme právě popsaný motor běžet pozpátku; „horký“ bude vzduch v místnosti a „studený“ bude vnitřek chladničky.
Takže zpět k výkladu: dokážeme nejprve ekvivalenci obou formulací 2. zákona termodynamiky:

Zapojíme-li tedy na perpetuum mobile 2. druhu chladničku, budeme nakonec bez dodávání práce přenášet teplo ze studeného prostředí do teplého – a to, bohužel, nejde podle druhé formulace.
Pokud bychom naopak uměli bez práce převádět teplo z chladné lázně do teplejší (což také neodporuje zákonu zachování energie!), stačilo by pak mezi ně napojit obvyklý tepelný motor (dostali byste předchozí obrázek „pozpátku“ – umíte si to sami nakreslit?), a měli bychom perpetuum mobile 2. druhu. Což zase nejde, tentokrát podle první formulace.
Tím máme ekvivalenci obou formulací úspěšně za sebou. a jak dál se zavedením teploty?
Nejdříve malé překvapení: účinnost všech vratných motorů pracujících mezi danými dvěma lázněmi je přesně stejná, nezávislá na konstrukci stroje! Jak je to možné? Podívejte se na první obrázek s motorem a chladničkou. Kdyby teploty lázní na obou obrázcích byly stejné a chladnička pracovala „obráceně“, jako motor, pak by měla menší účinnost (1/6) než motor vlevo (1/4). To je výborné – jejich propojením bych získal stroj, který by koneckonců za jeden cykl převedl 2 díly tepla ze studené do teplé lázně – ale to nedovoluje druhé znění 2. zákona termodynamiky. Pokud tedy oba stroje jsou vratné a pracují tak, jak, je uvedeno, pak mají různě teplé pracovní lázně!
Účinnost motoru je rovna podílu co dostanu/co zaplatím (obojí kladné – podle toho budou čárky). V tomto případě platím teplo Q2, dostávám práci W’, a účinnost je tedy (pozor na čárky u proměnných!)
η = 1 – (Q’1 / Q2 )< 1 .
Protože je dána jen teplotami lázní, lze zřejmě také naopak zavést teplotu (termodynamickou) podle této univerzální účinnosti: teplota lázně bude prostě úměrná množství vyměněného tepla. Kdyby na našem obrázku měly obě „studené lázně“ stejnou teplotu T1 = T’1 = 300 K, pak T2 = 400 K a T’2 = 360 K, aby byly zachovány poměry teplot a vyměněných tepel.
Aby nenastala vzpoura praktiků a techniků na celé zeměkouli, bylo pro zavedení termodynamické teploty potřeba
- rozumně zvolit dobře definovatelnou a reprodukovatelnou referenční teplotu,
- přiřadit jí takovou hodnotu v kelvinech, aby se kelvin co možná nelišil od stupně Celsia.
Což se prozatím podařilo tím, že za referenční teplotu se vzal trojný bod vody – tedy ta teplota, při níž může být spolu v rovnováze voda plynná (pára), kapalná i pevná (led), a protože mu v dosavadní Celsiově stupnici odpovídá teplota 0,01 °C, tak mu byla přiřazena teplota právě 273,16 K. Tím „bod mrazu“ 0 °C odpovídá 273,15 K, přírůstek 1 °C = 1 K a bod varu vody zůstal zhruba o 100 °C výš než bod mrazu. Po bitvě je každý generálem: kdybychom to tehdy určovali my se současnou přesností měření teploty, zvolili bychom 273,22, a vyšlo by to lépe. Ale za opravu to nestojí, protože bod varu vody (nyní za standardního tlaku 99,974 °C) není zas až tak důležitý, abychom trvali na přesných 100 °C. Větší problém je, že i ta nejčistší, „nejpředestilovanější a iontově nejvyměněnější“ voda může mít ještě různé izotopové složení, protože máme 2 typy vodíku (1H, 2D) a tři typy kyslíku (16O, 17O, 18O). Takže se pracuje na nové definici teploty, dané tak, aby si vhodná univerzální konstanta (zde to bude Boltzmannova konstanta k), zachovala dosavadní hodnotu.
Tím bychom měli slíbené za sebou; ale my ještě přidáme pilnému čtenáři dva pamlsky: praktikům připomeneme a přiblížíme tepelná čerpadla, teoretikům zavedeme entropii – míru chaosu.
Tepelné čerpadlo
Chladničku jistě znáte: uvnitř má mrazák s –20 °C, venku vzadu žebroví, které se hodně hřeje, a má ještě elektromotor. Ten stlačuje plyn, který se tím ohřívá, stlačený v žebroví se okolním vzduchem ochlazuje a pak se zpět uvnitř, v mrazáku, rozpíná; přitom se naopak ochlazuje hodně pod svou původní teplotu. Její chladicí faktor (rozlišujme „i – í“: „chladicí“ = týkající se chlazení, „chladící“ = ten, co právě teď chladí) je opět známý podíl (co dostanu) / (co zaplatím). v tomto případě platím dodanou práci W, dostávám „mrazáku odebrané teplo“ Q1, a účinnost je tedy
Chladicí faktor může být i větší, i menší než jednička.
Žebroví za chladničkou je vždy dosti teplé: musí vyzářit jednak všechnu dodanou elektrickou energii, jednak i to množství tepla, které musíme stále odčerpávat z mrazáku (kvůli nedokonalé izolaci), aby zůstal tak chladný, jak my si přejeme.
Tepelné čerpadlo z chladničky dostaneme tak, že chladničku postavíme v místnosti k oknu, žebrovím k nám, a mrazák vytáhneme až před dům, do potůčku tekoucího pod okny. Ten má i v zimě teplotu kolem 4 °C. „Chladnička“ – tepelné čerpadlo nyní tedy chladí potůček. Odebírá od něj teplo a převádí ho spolu s dodávanou elektrickou energií přes žebroví do našeho pokoje. Topný faktor tepelného čerpadla je i zde roven podílu (co dostanu) / (co zaplatím). v tomto případě platím práci W, dostávám teplo Q’2, a topný faktor je tedy k našemu potěšení vždy větší než 1 (uvažte proč!)
η = Q’2 / W = Q’2 / (Q’2 – Q1) = 1 + Q1 / (Q’2 – Q1)
Entropie
Převádíme-li za teploty T vratným způsobem teplo Q, pak můžeme zavést veličinu S = Q / T. Dříve se jí říkalo „redukované teplo“, nyní zavádíme entropii. Je to veličina extenzivní, entropie celého systému tedy je rovna součtu entropií jeho částí. (Exenzivní je taky třeba energie, objem, počet částic. U veličin intenzivních, jako je třeba tlak a teplota, je tomu v rovnováze jinak: např. tlak v celém objemu plynu je stejný jako tlak v každé jeho části, není to „součet dílčích tlaků“.) Entropie souvisí s pravděpodobností a tím i s chaosem: Samovolný vývoj směřuje vždy k více pravděpodobnému a tedy k „chaotičtějšímu“ stavu. Entropii můžeme zavést i hodně daleko od fyziky, totiž v informatice, a to stejným principem: entropie S je úměrná logaritmu pravděpodobnosti w, tedy
protože pro systém složený ze dvou nezávislých částí se pravděpodobnosti jeho částí násobí, zatímco jejich entropie se sčítají. Pravděpodobnost w stavu je přitom úměrná počtu různých mikrostavů (individuálních rozložení jednotlivých molekul tvořících systém), které se nám jeví jako stejný makroskopický stav.
Při vratných dějích se entropie nemění. Nevratné děje probíhají samovolně vždy tak, že entropie celku roste. (Entropie části může klesat, pokud dostatečně roste entropie nějaké jiné části systému.)
TŘETÍ ZÁKON TERMODYNAMIKY: NEDOJDEŠ NIKDÁŽ POŘÁDKU ÚPLNÉHO, LEČ JEN V POTU TVÁŘE SE TOMUTO BLÍŽITI SMÍŠ
Nebo tak stojí psáno v Knize knih Přírody: Každý pak systém, kterýž by sis kde vymyslil, jedině jeden jediný ze stavů všech svých takový má, žeť energií jsa nejchudší, však pořádkem nejbohatší jest, kterýžto stav pak teplotě nuly absolutní odpovídá, entropii pak taktéž nulovou maje.
Nebo tak stojí psáno v Knize knih Přírody: Každý pak systém, kterýž by sis kde vymyslil, jedině jeden jediný ze stavů všech svých takový má, žeť energií jsa nejchudší, však pořádkem nejbohatší jest, kterýžto stav pak teplotě nuly absolutní odpovídá, entropii pak taktéž nulovou maje.
Rozuměj:
„Snižovat
teplotu“ znamená „zmenšovat kinetickou energii“ chaotického pohybu
částic systému, a tím také zvyšovat uspořádanost systému. Každý
reálný systém má jediný stav s nejnižší energií; tomu přísluší
nejnižší entropie (neuspořádanost) a nejnižší teplota; obě lze
položit rovny nule jako základ stupnice. Tento stav je nedosažitelný
konečným počtem kroků; můžeme se mu jen blížit. Také účinnost všech
chladicích postupů se snižuje tak, jak se tomuto stavu („absolutní
nule“) blížíme.
Tady je to celkem srozumitelné. (Pravda, uklízejíce pokoj svůj pod dozorem rodičů svých, pozorujeme to a cítíme to jako křivdu od přírody, ale co se dá dělat.)
Makrostav systému v „naprostém pořádku“, bez jakékoli energie navíc, je realizován pouze jedním jediným mikrostavem, v němž je každá molekula systému „na svém místě“ (ve ztuhlém krystalu látky) a v klidu. Protože je tento mikrostav jediný, je pravděpodobnost jeho výskytu v tomto makrostavu „naprostého pořádku“ dána jistotou – je rovna jedné. Proto je entropie tohoto makrostavu rovna nule, log 1 = 0. Energie je vskutku nejmenší a můžeme ji tedy také položit rovnu nule. Můžete se ptát, jak to je s Einsteinovou energií E = m c2. Tu zde neuvažujeme proto, že ji nemůžeme nijak od systému odebrat. Pokud ji tedy bude mít systém stejnou vždy a všude, pak se neprojeví v žádných rozdílech energií udávajících teplo, práci, anebo chemickou práci, a nemusíme ji uvažovat vůbec.
Tento zákon jaksi „završuje“ celou trojici. Druhý zákon umožnil zavést objektivní nezávislou teplotu, a to i s její „počáteční hodnotou“; naproti tomu u entropie (např. u redukovaného tepla) šlo vždy jen o děj, kterým se entropie zvětšovala nebo zmenšovala. „Počáteční hodnota“ však chyběla. Tu tedy nyní stanovuje třetí zákon termodynamiky.
Teoretická nedosažitelnost onoho jediného stavu s minimální energií souhlasí s jeho praktickou nedosažitelností. Připomeňme např. náš dosavadní systém chlazení (s rozpínáním plynu tak, aby přitom konal práci a nedostával teplo). Snížení teploty je úměrné příslušnému snížení energie (vykonané práci), a činitel úměrnosti je měrné teplo plynu. To se ale u skutečných látek při velice nízkých teplotách také blíží nule, takže proces ochlazování je čím dále, tím méně účinný (nehledě na to, že každý skutečný plyn dostatečným ochlazením zkapalní až ztuhne).
Představíme-li si systém s nenulovou teplotou jako předměty v kočáře kodrcajícím přes hrubou kamennou dlažbu, pak „ochladit“ znamená vytvořit v kočáře prostředí, kde by věci byly ve větším klidu. Ve Vesmíru je velmi mnoho hvězd, které jsou uvnitř tak horké, jak na Zemi zatím neumíme nic zahřát (a snažíme se o to, umožnilo by nám to termojadernou fúzi jako zdroj energie!). Naproti tomu mezihvězdný prostor rozpínáním Vesmíru už jen chladne a v současnosti má jen pouhých 2,7 K. Protože podle 2. zákona termodynamiky se nemůže předmět bez dodávání práce ochladit pod teplotu svého okolí, můžeme být plným právem pyšní na to, že u nás na Zemi, v každé laboratoři nízkých teplot, máme k dispozici něco, co není nikde jinde ve Vesmíru (tedy nikde tam, kde zelení mužíčkové nemají své experimentální laboratoře nízkých teplot).
Doporučená literatura k tématu:
Standardní učebnice termodynamiky nebo fyzikální chemie z libovolného nakladatelství odborné či pedagogické (nikoli alternativní!) literatury.
Na webu, jako obvykle,. Wikipedie: http://cs.wikipedia.org/wiki/Termodynamický_zákon
(napsat s diakritikou!)
Pozn. autora: Zatímco perpetuum mobile 1. druhu už vynálezce omrzelo, 2. zákon termodynamiky nachází stále své „přemožitele“. Pokud se totiž místo skutečného pokusu jen citují jiní „přemožitelé“, využívá se „éterická energie“ apod., pak lze všelicos, viz např. týž článek na třech různých adresách
http://www.upramene.cz/energie/view.php?cisloclanku=2006112301
http://www.atlantislabs.sk/peter-lindemann-termodynamika-a-volna-energia?page=2
http://www.mwm.cz/clanek1.php?id=120&pjmeno=&kredit=&p1=
Doc. Jan Obdržálek

Perpetuum mobile je utopie. Příklad jednoho z nich - Perpetuum mobile Johanna Ernsta Eliase Besslera z roku 1719 (a my bychom upřesnili: perpetuum mobile 1. druhu)