Funkce, co něco počítají
Velmi často narazíme na situaci, kdy je potřeba spočíst hodnotu nějakého výrazu závislého na parametrch. Funkce jsou správným způsobem zápisu takového kódu, a v programování je tedy chápeme podobně jako v matematice.
Pokud tedy potřebujeme pracovat s výrazem
je rozumné si jej označit nejakou zkratkou. Pokud tak činíme v rámci programování, znamená to jako součást našeho programu definovat funkci a tu pak na příslušném místě použít.
Nutno zdůraznit, že takový postup je správný, i když funkci používáme jen na jednom místě: * Jakmile jde o netriviální vzoreček, protože to povede k zpřehlednění kódu. V případě delšího vzorečku navíc bude režie související s voláním funkce zanedbatelná. * Kdykoli izolace takového výpočtu znamená zpřehlednění kódu (\(\implies\) méně chyb). * Pokud výpočet vzorce vyžaduje pomocné proměnné, stanou se z nich lokální proměnné a nepřekáží. * Protože funkci lze většinou testovat nezávisle na dalším kódu.
Již víme, jak funkci napsat a že vzoreček výše můžeme přepsat takto
[ ]:
def moje_funkce(x,n):
"Sčítá n členů mocninné řady x^k/(k^2+1)"
soucet = 1
xk = 1
for k in range(1,n+1):
xk = xk*x
soucet = soucet + xk/(1+k*k)
return soucet
moje_funkce(1/2,1)
1.25
Protože přepisování vzorečků do podoby funkcí v nějakém programu je častá činnost, rozeberme si podrobněji, co takový proces zahrnuje.
Nejprve musíme identifikovat vlastnosti vzorečku, které určují podobu kódu
konstanty (a zda je chápat jako lokální nebo globální)
parametry + typy parametrů (celá čísla, reálná, komplexní, vektor, pole, ....)
druhy a meze cyklů resp. podmínky jejich ukončení
optimalizace
S uvážením výše uvedených hledisek přepsat vzorec do podoby kódu.
Optimalizaci budeme uvažovat jen naprosto elementární:
opakující se podvýrazy
pokud se ve vztahu vyskytují hodnoty \(1,x,x^2,...x^n\) nepotřebujeme mocnění, stačí nám v každém kroku spočíst (viz výše)
xk = xk*xpodobně \(1!, 2!, 3!, ... n!\) počítáme pomocí opakovaným násobením
kfakt = kfakt*kv obou případech nesmíme zapomenou na inicializaci např.
xk=1další varianty téhož jsou např. pokud se v \(\sum_k\) nebo \(\prod_k\) objevují \(x^{2k+1}\), \(k!!\) atp.
Méně elementární optimalizací je postupný výpočet \(\sin(x), \sin(2x), ...\sin(n x)\). Ten lze pomocí součtových vzorců redukovat na násobení (ano, i když musíme navíc počítat i \(\cos(kx)\), stejně se to vyplatí)
To, kdy místo jednoho vzorce vezmeme jiný, efektivnější, již nespadá do programování. Příklad potkáte na Prosemináři matematické fyziky u výpočtu velkých Fibonacciho čísel:
Příklad jednoduché funkce dané vzorečkem
\(\displaystyle h(n) = \sum_{k=1}^n \frac{1}{k}\)
Pozorování: je to funkce celočíselného argumentu a vrací reálné číslo. V Pythonu není povinností typ argumentu ani výsledku explicitně uvádět. Proto vystačíme s kódem
[ ]:
def harmonic(n):
"""Vrací hramonická čísla h_n pro celé n>=0"""
s = 0.0
for k in range(1,n+1):
s = s+1/k
return s
Při psaní tohoto kódu byl zřejmý postup výpočtu doplněn o minimální docstring. Bylo také nutno nějak zvolit název funkce a identifikátory lokálních proměnných a zvážit, zde se projeví, když n není celé, a jestli to musíme hlídat. (Rozmyslete+vyzkoušejte.)
Potenciální chyba: pro záporná n vrací bez protestu 0.
Složitější funkce
Pro obvod elipsy s poloosami \(a,b\) snadno najdeme vzorec
kde např. \(7!! = 1.3.5.7\) a \(\epsilon^2 = 1-b^2/a^2\). Protože sčítatr nekonečně členů nelze, obsahuje funkce dodatšný parametr rtol stanovující akceptovatelnou relativní chybu. Podmínka 2*abs(ds)<rtol*(1-eps2) je odhadnuta na základě vzroce pro zbytek geometrické řady s přidanou rezervou 2x.
Navíc s použitím tzv. eliptických funkcí je možné psát \(O = 4a E(\epsilon^2)\), kde \(E\) nalezeneme jako funkci elipe v scipy.special místo v math.
Vidíme dva různé postupy dávajcíí v rámci tolerance stejný výsledek.
[ ]:
import math
import scipy.special
def obvod_elipsy(a, b, rtol=1e-10):
if b>a:
a,b = b,a
assert 3e-12 < rtol < 0.1, "Parametr rtol mimo rozumný rozsah."
eps2 = 1-b**2/a**2
max2k = 1_000_000
s = 1
f2 = 1
dve_k = 2
while dve_k<max2k:
f2 = f2*((dve_k-1)/dve_k)**2 * eps2
ds = f2/(dve_k-1)
s = s-ds
dve_k = dve_k+2
if 2*abs(ds)<rtol*(1-eps2):
return 2*math.pi*a*s
assert False, "Soucet rady nekonverguje"
def obvod_elipsy_presne(a, b):
""""Výpočet obvodu elipsy s použitím eliptických integrálů z knihovny scipy"""
eps2 = 1-b**2/a**2
return 4*a*scipy.special.ellipe(eps2) # zajímavost: funguje i pro eps2<0, proto nezkoumáme zda a>b
obvod_elipsy(1,0.005)/obvod_elipsy_presne(1,0.005) - 1
6.292877330338342e-11
[ ]:
# Ukázka argumentů, pro které assert funkce selže
ae = 1
be = 0.0001
obvod_elipsy(ae,be)/obvod_elipsy_presne(ae,be) - 1
Polynomy a Hornerovo schéma
Další obvyklou formou v níž může být užitečný vzorec zapsán je polynomiální aproximace.
Zde si ukážeme, že pro výpočet hodnoty polynomu nepotřebujeme mocnění, pokud použicjeme chytře závorky protože existuje tzv. Hornerovo schéma
Komenář ke kódu
funkce kontroluje platnost předpokladů pomocí
assertvýrazy mohou pokračovat na dalším řádku, pokud je nový řádek uvnitř závorek
Hornerovo schéma v proměnné
eps2Duhové závorky v editoru
Koeficienty se naučíte získat v jiných předmětech
[ ]:
def obvod_elipsy_maleeps(a, b):
if b>a:
a,b = b,a
eps2 = 1-b**2/a**2
assert eps2<0.2, f"aproximace vyžaduje eps2<0.2, ale eps2={eps2:4.2g}"
return 2*a*(3.141592653589794 +
eps2*(-0.7853981633973549 + eps2*(-0.14726215563710238 +
eps2*(-0.06135923157099829 + eps2*(-0.03355582977261537 +
eps2*(-0.021140163218417073 + eps2*(-0.014533859052562739 +
eps2*(-0.010604501590171097 + eps2*(-0.008077869381533908 +
eps2*(-0.006330939782841333 + eps2*(-0.005106344943641083 +
eps2*(-0.004691669404826085 - 0.003988570536164187*eps2))))))))))))
obvod_elipsy_maleeps(1, 0.9)/obvod_elipsy_presne(1,0.9) - 1
2.220446049250313e-16
Testujeme funkce
Poté, co kód funkce napíšeme je na místě vyzkoušet, jestli jsme někde neudělali chybu. Víme, že toto nebudeme zkoumat na úrovni matematického důkazu, ale spíše empiricky. Základním důvodem nepřeskočit testování nějaké funkce je fakt, že nám to ušetří práci později, až nebude fungovat program, který funkci používá.
Již jsme viděli, příklad situace, kdy máme dvě alternativní funkce počítající tentýž výraz. Pak můžeme zkoumat
zda dávají stejné výsledky
kdy je která efektivnější (rychlejší)
Většinou ale máme ale jen jednu funkci, pak můžeme
Nakreslit graf funkce pro vhodný rozsah parametrů. Stojí za to, tak učinit podrobně v okolí problematických bodů.
Srovnat hodnoty ve vybraných bodech s hodnotam z tabulky či jiných zdrojů (např. Wofram Alpha).
Zkontrolovat zda funkční hodnoty splňují nějakou identitu, která pro danou funkci platí, např. \(\Gamma(x+1)=x \Gamma(x)\).
Příklad demostrující doktrínu strukturovaného programování
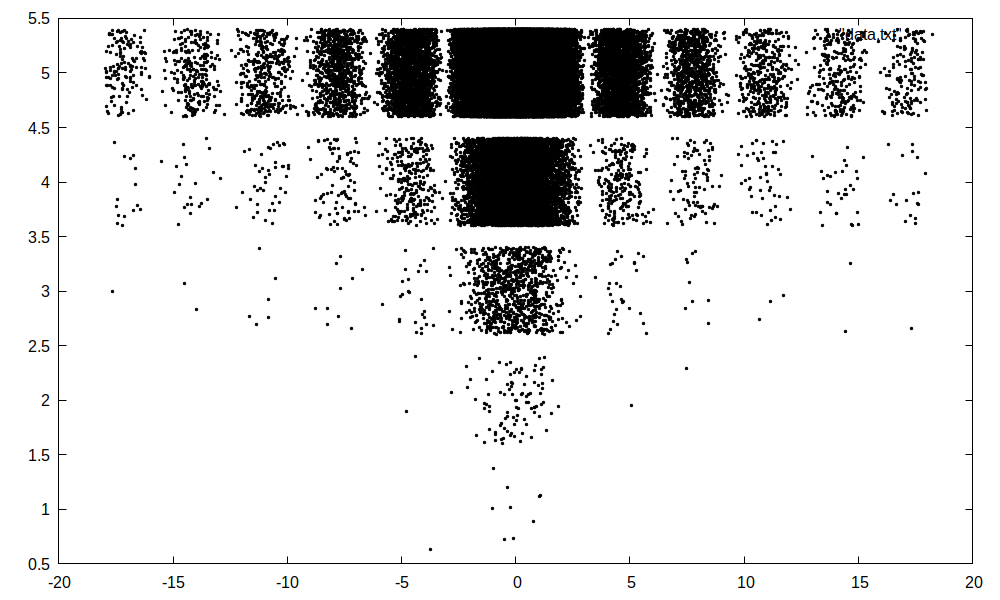
Následují dva programy vykreslující statistiku interferenčního obrazce. Ten druhý demonstruje doktrínu strukturovaného procedurálního programování tím, že kód je rozdělen na hlavní program a dvě funkce.
Interferneční obrazec je dán hustotou pravděpodobnosti, kterou popíšeme nějakoou modelovou funkcí, např.
Program generuje náhodné hodnoty respektující \(p(x)\) a to tak, že pro náhodné \(x\) spočte \(p(x)\) a pak si "hodí kostkou" a s pravěpodobností \(p(x)\) danou hodnotu \(x\) přijme (a tedy s pravěpodobností \(1-p(x)\) tuto hodnotu \(x\) zahodí).
Program je doplně kódem pro Jupyter uvedeným v bodech 2-4, který výstup programu uložený v souboru "data.txt" vykreslí a zobrazí.
[ ]:
## 1. kód vytvářející textový soubor s tabulkou čísel
import random
import math
# rozměry stínítka interferenčního obrazce
a = 18
deset_na_p = 10
with open("data.txt","w") as f:
for p in range(1,6):
n = 0 # počet dopadů na stínítko
while n < deset_na_p:
x = -a + 2*a*random.random() # náhodná souřadnice x z intervalu <-a,a>
if math.sin(x)**2 > random.random()*x*x: # dopadne zde ?
y = -0.4 + 0.8*random.random() + p # náhodná souřadnice y
print(x, y, file=f)
n = n + 1
print(end="\n\n", file=f)
deset_na_p = deset_na_p * 10
## 2. kód vytvářející skript pro gnuplot
gnuplot_skript = """
set term pngcairo size 1000,600 enhanced font "Arial,12.0" # font je nutno specifikovat!
set output "obrazek.png"
plot "data.txt" linecolor "black" pt 7 ps 0.4
"""
with open("prikazy.gp","w") as f:
print(gnuplot_skript, file=f)
## 3. kód spouštějící gnuplot
!gnuplot prikazy.gp
## 4. kód zobrazující vytvořený obrázek
from PIL import Image
display(Image.open("obrazek.png"))
[ ]:
## 1. kód vytvářející textový soubor s tabulkou čísel
import random
import math
# rozměry stínítka interferenčního obrazce
a = 18
def pravdepodobnostni_funkce(x):
"funkce p(x)= ( sin(x)/x )^2"
# POZOR: funkce musí mít obor hodnot spadající do intervalu (0,1)
if x==0:
return 1
return (math.sin(x)/x)**2
def nahodny_bod():
"generuje nahodna x,y respektujici hustou pravdepodobnosti p(x)"
b = 0.4
while True:
x = -a + 2*a*random.random() # náhodná souřadnice x z intervalu <-a,a>
hod_kostkou = pravdepodobnostni_funkce(x) > random.random()
if hod_kostkou:
y = -b + 2*b*random.random() # náhodná souřadnice y z intervalu <-b,b>
return x,y
with open("data.txt","w") as f:
for p in range(1,6):
for n in range(10**p):
x,y = nahodny_bod()
print(x, y+p, file=f)
print(end="\n\n", file=f)
## 2. kód vytvářející skript pro gnuplot
gnuplot_skript = """
set term pngcairo size 1000,600 enhanced font "Arial,12.0" # font je nutno specifikovat!
set output "obrazek.png"
plot "data.txt" linecolor "black" pt 7 ps 0.4 notitle
"""
with open("prikazy.gp","w") as f:
print(gnuplot_skript, file=f)
## 3. kód spouštějící gnuplot
!gnuplot prikazy.gp
## 4. kód zobrazující vytvořený obrázek
from PIL import Image
display(Image.open("obrazek.png"))
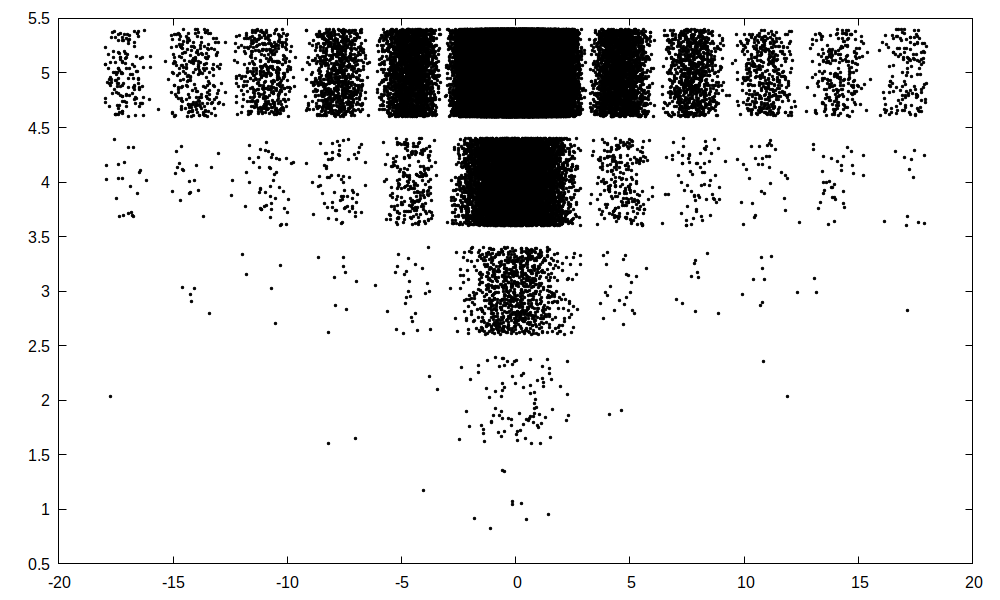
Porovnejme oba kódy abychom ocenili, že rozdělení kódu do funkcí přináší vyšší srozumitelnost 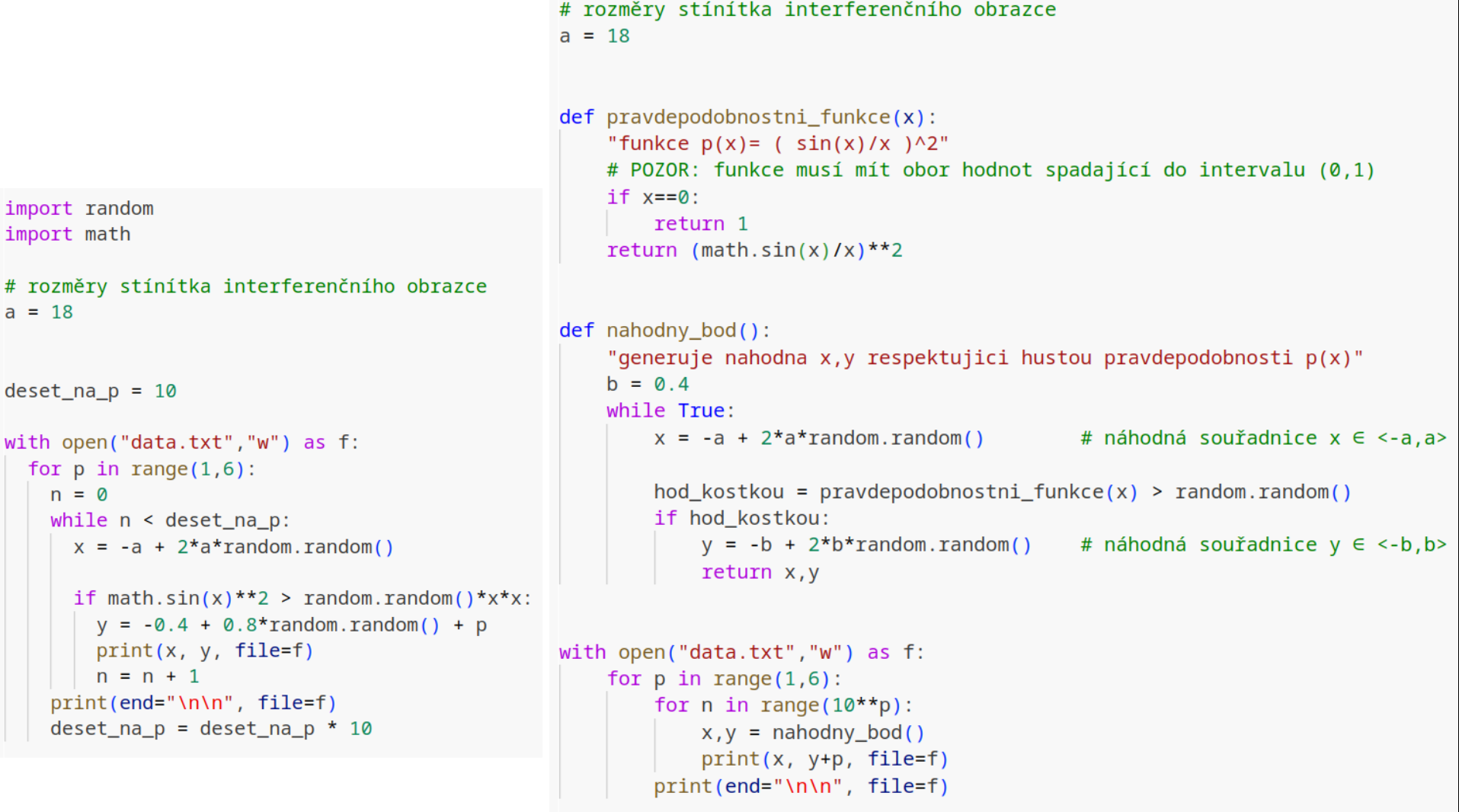
Funkce definované rekurentními vztahy
Dobře známe rekurzivní definici faktoriálu:
Tu do podoby funkce přepíšeme takto
def faktorial(n):
"Výpočet faktoriálu rekurzí"
assert n >= 0
if n == 0:
return 1
return n * faktorial2(n-1)
Podobně můžeme psát pro Fibonacciho posloupnost
tedy
[ ]:
def fib(n):
assert n>=0 and type(n) == int
if n<2:
return n
return fib(n-1) + fib(n-2)
print(fib(35))
9227465
Pro větší hodnoty argumentu je ale funkce velmi pomalá a v určitý okamžik bychom ji překonali ručními výpočty. To proto, že bychom použili lineární algoritmus. Jeho varianta v podobě funkce vypadá takto:
[ ]:
def fib(n):
"Fibonacciho posloupnost, n-tý člen"
assert n>=0
if n == 0:
return 0
a, b = 0, 1
for i in range(2, n+1):
a, b = b, a+b
return b
Pokud bychom neměli k dispozici vícenásobné přiřazení (může se vám hodit např. v C), pak by kód vypadal takto
[ ]:
def fib(n):
"Fibonacciho posloupnost, n-tý člen"
assert n>=0
if n == 0:
return 0
a = 0
b = 1
for i in range(2, n+1):
c = a + b
a = b
b = c
return b
Mohlo by se zdát, že zbytečně věnujeme spoustu času nudným Fibonacciho číslům, nicméně ve fyzice (nejen té matematické) potřebujeme často např. Legenderovy poynomy. Ty jsou podobně jako jiné důležité funkce dány formulí podobnou Fibonacciho:
pričemž tato rekurentní formule začíná
[ ]:
def legendreP(n, x):
"Legenderův polynom"
assert n>=0
if n == 0:
return 1
a = 1
b = x
for i in range(2, n+1):
c = ((2*k-1)*x*b-(k-1)*a)/k
a = b
b = c
return b
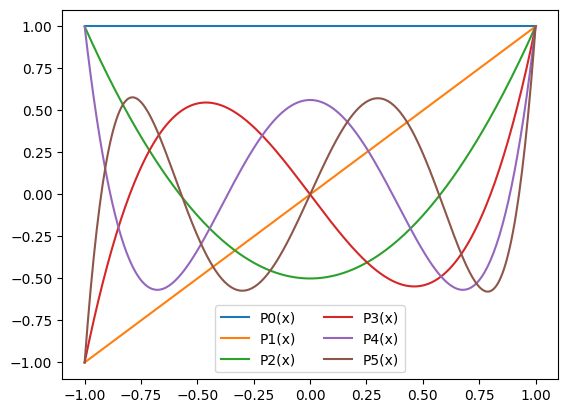
Abychom mohli pohodlně ocenit pohlednost těchto polynomů použijeme v následujícím kódu funkci grafFunkce, která namaluje funkci, kterou jí předáme jako argument. Jak to dělá se ale dozvíme později.
[1]:
import matplotlib.pyplot as plt
import numpy as np
def grafFunkce(f, a=0, b=1, n=300, show=False, arg1=None, arg2=None, **opts):
"""
Namaluj graf f(x) pro x z intervalu <a,b>
Jako volitelné argumenty lze užít např.
c|color, ls|linestyle, lw|linewidth
viz: https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html
show = True .... vynutí vykreslení grafu, nečeká se na konec buňky.
arg2 = a ... graf funkce f(x,a)
arg1 = b ... graf funkce f(b,x)
"""
xVals = np.linspace(a,b,n)
if arg1 is None and arg2 is None:
yVals = [f(x) for x in xVals]
elif arg1 is None:
yVals = [f(x, arg2) for x in xVals]
elif arg2 is None:
yVals = [f(arg1, x) for x in xVals]
else:
yVals = [f(arg1, arg2, x) for x in xVals]
plt.plot(xVals, yVals, **opts)
if show:
plt.show()
[ ]:
for k in range(0,6):
grafFunkce(legendreP, -1, 1, arg1=k, label=f"P{k}(x)") # graf
leg = plt.legend(loc='lower center', ncols=2) # jen pro informaci
Hledání kořenů funkcí, metoda půlení intervalu
Mnoho funkcí je definován jako řešení nějaké rovnice. Například odmocnina. Proto si ukážeme dvě metody hledání kořenů a jak je použít v definici nové funkce.
Začneme metodou jednoduchou, spolehlivou a často postačující svým výkonem. Je založena na faktu, že spojitá funkce musí mít mezi dvěma body, kde nabývá opačného znaménka nějaký kořen. Spočte proto, jaké znaménko má funkce uprostřed dného intervalu a podle znaménka pak zúží hledání na levou nebo pravou polovinu intervalu. Pak se postup opakuje, dokud není interval dost malý, aby nám libovolný jeho bod stačil jako odhad kořene funkce. Protože délka intervalu se s počtem kroků zmenšuje jako \(2^{-n}\), nebudeme takových půlení při rozumném počátečním odhadu intervalu potřebovat příliš (\(2^{-10}=1/1024\approx 10^{-3}\), tedy \(2^{-50}\approx 10^{-15}\)).
Definujeme si nejprve vhodnou funkci:
[3]:
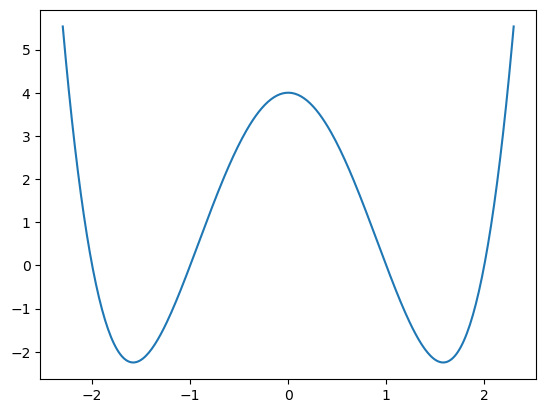
def f(x):
x2 = x*x
return (x2 - 4)*(x2 - 1)
grafFunkce(f, -2.3, 2.3)
[4]:
def koren_f(a,b, eps=1e-12):
fa = f(a)
fb = f(b)
assert fa*fb<0, "Metoda půlení intervalu vyžaduje opačná znaménka na koncích intervalu"
while abs(b-a)>eps:
c = (a + b) / 2 # spocti pulku intervalu
fc = f(c) # spocti funkci honotu tam
if fc ==0:
return c
if fa*fc > 0:
a = c # podle znamenka uprav meze intervalu
fa = fc # není nutné
else:
b = c
fb = fc
return (a+b)/2
koren_f(0,1.5)
[4]:
1.0000000000001137
V následujícím kódu modifikujeme funkci `f(x)`` tak, aby kreslila puntíky v místech, kde se ptáme na její funkční hodnotu. Můžeme pak vidět, jak metoda postupuje.
[10]:
f_kresli_xy = False
def f(x):
x2 = x*x
y = (x2 - 4)*(x2 - 1)
if f_kresli_xy:
plt.plot([x,x],[0,y],'-')
return y
grafFunkce(f, -2.3, 2.3)
f_kresli_xy = True
koren_f(-0.9,1.9)
[10]:
1.0000000000000453
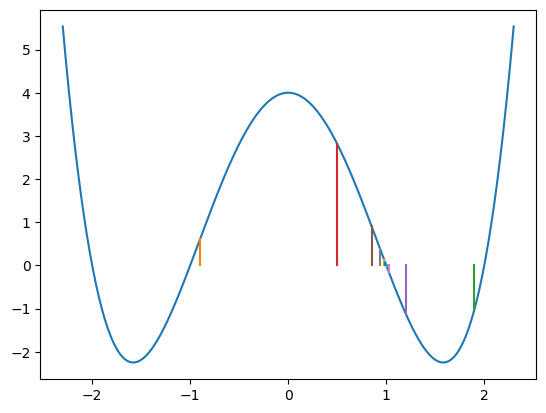
Na předchozím příkladě byl zajímaný také způsob, jak jsme funkci f předali informaci, zda má malovat úsečky znázorňující postup půlení. Použili jsme globální proměnnou f_kresli_xy. Připomeňme si, že pokud tuto neměníme, nemusíme uvnitř funkce psát 'global f_kresli_xy`.
Newtonova metoda hledání kořene (metoda sečen)
Ta spočívá v nahrazení funkce její tečnou v bodě \(x_k\), popsanou rovnicí \(f_{\rm tec}(x)=f(x_k)+f'(x_k)(x-x_k)\), pro niž lze snadno spočíst hodnotu kořene.
Tento postup opakujeme dokud nedostaneme dostatečně přesný odhad kořene.
Zatím se následujícímu kódu budeme věnovat jen z hlediska toho, že
definuje dvě funkce, které vrací \(f(x)\) a \(f'(x)\)
ve dvou krocích provede Newtonův postup hledání kořene
vytiskne výsledek
Doporučení: změňte x0 podívejte se jak se změní obrázek.
Až se seznámíme s poli a knihovnou matplotlib, vrátíme se k tomuto kódu z hlediska programování:
stanoví rozpětí vertikální osy, která bude na grafu vidět. Polynom 4. stupně nabývá rychle velkých hodnot a je třeba rozsah grafu takto omezit.
namaluje graf funkce \(f(x)\)
namaluje graf tečny (vzorec rovnice tečny je uveden výše, o výpočet příslušných hodnot se postará funkce
tecna0(x).)namaluje osu x
namaluje puntíky tam, kde se nacházejí \(x_0, x_1, x_2\). (Tak se ilustruje chování Newtonovy metody.)
[16]:
def f(x):
return (x*x-4)*(x*x-1)
def f1(x):
return x*(4*x*x-10)
x0 = 0.5
x1 = x0 - f(x0)/f1(x0)
x2 = x1 - f(x1)/f1(x1)
print(f"{x0} --> {x1} --> {x2:6.4f}")
def tecna0(x):
return f(x0) + f1(x0)*(x-x0)
plt.ylim(-5,8) # nastavení rozsahu osy y
grafFunkce(f, -2.5, +2.5) # graf f(x)
grafFunkce(tecna0, -2.5, +2.5) # graf tečny
plt.axhline() # namaluj osu x
plt.plot([x0],[f(x0)],'o') # puntík na souřadnice {x0,f(x0)}
plt.plot([x1],[f(x1)],'o') # {x1,f(x1)}
plt.plot([x2],[f(x2)],'o') # {x2,f(x2)}
plt.show()
0.5 --> 1.125 --> 0.9942
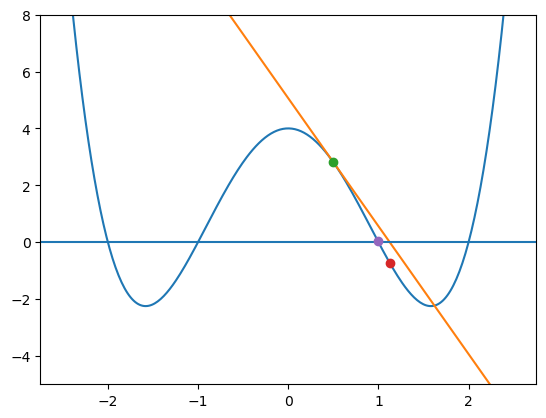
Úloha Změňte v úloze výše hodnotu x0 a podívejte se, jaký kořen (pokud vůbec) ve dvou krocích najde.
Úloha Vyzkoušejte, že v úplné blízkosti kořene metoda tečen každým krokem zhruba zdvojnásobí počet platných míst.
Teď, když jsme vyzkoušeli, jak metoda tečen funguje můžeme napsat funkci, která najde kořen nějaké funkce.
Požadujeme
musí hledat kořen libovolné funkce
bod, kde začít, dostane také jako argument
funkce musí poznat, že kořen nenašla
[135]:
def rootNewton(ff1, x0, rtol=1e-8, atol=1e-12, maxIter=20):
"""
Provede nanejvýš maxIter kroků Newtonovy metody.
ff1 ... Funkce a její derivace (předávají se společně).
x0 ... počáteční odhad kořene
rtol, atol ... požadovaná relativní absolutní chyba kořene
Výchozí hodnoty by obvykle měly dát 14 cifer pro kořen v okolí 1
"""
n = 0
x = x0
while True:
n = n+1
assert n<maxIter, "Překročen maximální počet iterací při hledání kořene."
f, f1 = ff1(x)
dx = -f/f1
x = x + dx
delta = max(atol, abs(rtol*x))
if abs(dx) < delta:
return x
def f_f1(x):
"Vrací f(x) a f'(x). f má kořeny -2,-1,1,2."
x2 = x*x
return (x2-4)*(x2-1), x*(4*x2-10)
rootNewton(f_f1, 0.5)
[135]:
1.0
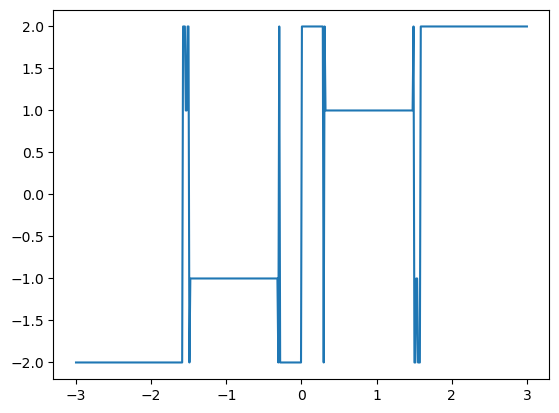
Zajímavost: Můžeme si namalovat, u kterého kořene skončí Newtonova metoda, když začneme s různými hodnotami počátečního odhadu polohy kořene. Vyplývá z toho, že je dobrá znát přibližně polohu kořene.
[40]:
grafFunkce(rootNewton, -3, 3, arg1=f_f1, n=498)
Inverzní funkce
Nyní uvedené metody hledání kořenu použijeme. Jedním ze způsobů, jak definovat funkci je zadání rovnice, kterou řeší. Místo abstraktní formulace vezměme konkrétní příklad:
Hledáme hodnotu \(y\) takovou, že pro dané \(z\in (-e^{-1},\infty)\) řeší rovnici \(z = y e^y\).
Máme dvě možnosti
použijeme nějakou funkci pro hledání kořene definované výše
napíšeme vše znovu (díky specializaci může být pak funkce rychlejší)
Z hlediska programování je zajímavější první varianta, protože musíme nějak zařídit, aby se hodnota \(z\) předala funkci, která bude počítat \(f(x) = x e^x - z\) a její derivaci \(f'(x) = (x+1) e^x\). Zvolíme nejjednodušší variantu, použijeme globální proměnnou.
[147]:
import math
param_z_W = 0.0
def f_f1_W(x):
"Vrací f(x) a f'(x) pro f=x e^x-z"
ex = math.exp(x)
return x*ex - param_z_W, (x+1)*ex
def lambertW(x):
"Lambertova funkce W(x). Řeší rovnici y e^y == x. Def. obor je x > -1/e."
xe1 = x*math.e+1
if xe1 == 0:
return -1
assert xe1 > 0, f"Argument {x=} neleží v definičním oboru W(x)"
# volba počátečního odhadu kořene
if x>10:
x0 = math.log(xe1)
elif x>0:
x0 = 0.5*math.log(xe1)
else:
x0 = 0
# před zavoláním rootNewton nutno nastavit globální proměnnou param_z_W
global param_z_W
param_z_W = x
y = rootNewton(f_f1_W, x0, maxIter=50)
assert y > -1, "interní chyba lambertW, nalezen kořen na druhé větvi!"
return y
# test
x_test = 0.3
y_test = lambertW(x_test)
print( f"W({x_test}) = {y_test}, rel.chyba = {y_test*math.exp(y_test)/x_test - 1:5.1e}" )
W(0.3) = 0.23675531078855933, rel.chyba = 2.2e-16
Reálná čísla v počítači
kde \(s=\pm 1\), \(0\le m \le 2^{53}-1\) a \(|e|<2^{1024}\) představují složky zápisu čísla zvané znaménko, mantisa a exponent. Stroj pak sbalí všechnu tuto informaci do 64 bitů a pracuje s ní najednou jako jediným "reálným" číslem.
0011111111110000000000000000000000000000000000000000000000000000
1.000000000000 = +1.0000000000000000000000000000000000000000000000000000 x 2^(0)
1100000000100000000000000000000000000000000000000000000000000000
-8.000000000000 = -1.0000000000000000000000000000000000000000000000000000 x 2^(3)
0100000000100010000000000000000000000000000000000000000000000000
9.000000000000 = +1.0010000000000000000000000000000000000000000000000000 x 2^(3)
0100000000001001001000011111101101010100010001000010110100011000
3.141592653590 = +1.1001001000011111101101010100010001000010110100011000 x 2^(1)
0011111110111001100110011001100110011001100110011001100110011010
0.100000000000 = +1.1001100110011001100110011001100110011001100110011010 x 2^(-4)
[155]:
import math
for x in [1.0, -8.0, math.pi, 0.1]:
print(f"{x.hex():>22} ({x})")
0x1.0000000000000p+0 (1.0)
-0x1.0000000000000p+3 (-8.0)
0x1.921fb54442d18p+1 (3.141592653589793)
0x1.999999999999ap-4 (0.1)
Například \(\pi\) je tedy nahrazeno aproximací
vzhledem k tomu, že čitatel může mít nejvýš 16 dekadických cifer, dá se říct, že reálná čísla a výpočty s nimi jsou k dispozici jen (necelými) 16 platnými ciframi. Protože mocniny desíti nejsou mocninami dvojky, racionální čísla \(0.1=1/10, 0.99=99/100\), atp. mající konečný dekadický zápis, mají binární zápis nekonečný (podobně jako třeba číslo \(1/3\)) a tedy nejsou v proměnné typu float uložena přesně.
Skutečnost, že místo reálných čísel máme jen velmi malou podmnožinu čísel racionálních znamená, že výsledek každé operaci je většinou znám jen v zaokrouhlené podobě. Obvykle platí, že výsledek takové operace je zatížen podobnou chybou jako veličiny do operace vstupující. Důležitou výjimkou jsou operace sčítání, odečítání (a složitější, například trigonometrické funkce sčítání implicitně obsahující):
1.0000000000123456
-1.0000000000000000
---------------------
0.0000000000123456 -> 1.23456E-11
Výsledek tedy najednou představuje číslo s pouhými šesti platnými ciframi. Přesně tento problém nastane při použití známého vzorečku pro kořen kvadratické rovnice. Stačí si prohlédnout tabulky integrálů nebo speciálních funkcí, aby člověk zjistil, jak často se rozdíl blízkých veličin počítá, např. \(1-\sqrt{1-x^2}\) pro malá \(x\). Existují situace, kdy ztráta přesnosti je extrémní:
[157]:
from math import cos
for i in range(7):
x = 2/10**i
f1 = (1 - cos(3*x) - cos(4*x) + cos(5*x))/(1 - cos(x))**2
f2 = 4*(3 + 5*cos(x) + 3*cos(2*x) + cos(3*x))
print( f"{x=:6} {f1=:15.12g} {f2=:15.12f} {f1-f2:8.1e}" )
x= 2.0 f1=-0.325979034705 f2=-0.325979034705 1.2e-15
x= 0.2 f1= 45.9554059445 f2=45.955405944498 3.9e-13
x= 0.02 f1= 47.9792035724 f2=47.979203573004 -6.0e-10
x= 0.002 f1= 47.9997750673 f2=47.999792000357 -1.7e-05
x=0.0002 f1= 48.0171463987 f2=47.999997920000 1.7e-02
x= 2e-05 f1= 2775.55710226 f2=47.999999979200 2.7e+03
x= 2e-06 f1= 0 f2=47.999999999792 -4.8e+01
Povšimněte si, že zdrojem chyby ve výpočtu f1 je, jak bylo zmíněno výše, odečítání dvou blízkých čísel. Výraz f2 je ekvivalentní f1, ale k tomuto problému v něm v okolí \(x=0\) nedochází.
Je několik postupů jak obejít tento problém. Vynecháme-li ty, co vyžadují hluboké znalosti reprezentace reálných čísel v počítači, je potřeba nalézt alternativní formu daného výrazu. Někdy to jsou aplikace rozvojů, ovšem zmiňovaný výraz \(1-\sqrt{1-x^2}\) pro malé \(|x|\) stačí upravit jako \(x^2/(1+\sqrt{1-x^2})\) a podobně u oné kvadratické rovnice stačí úprava výrazu
kde při výpočtu volíme ten vztah, kdy oba sčítance mají stejná znaménka a tedy nedojde ke ztrátě platných cifer.
Kontrolní úlohy
Zaokrouhlovací chyby v triviálních vzorcích
Pro \(m=1000\rm ~kg\) a \(v=100\rm ~km/h\) spočtěte
\[E_\text{kin} = \frac12 m v^2\]Zvažte možnost definovat konstanty
km=1000ahodina=3600(a pokud chcete dodržet etiketu, použijte pro konstanty velká písmena).Totéž pro Einsteinův vzorec
\[E_\text{kin} = \frac{m c^2}{\sqrt{1-\frac{v^2}{c^2}}}-m c^2\]Povšimněte si, že hodnoty nebudou moc souhlasit. Použijte trik, který byl doporučen pro odmocniny a ukažte, že relativistická kinetická energie dává pro automobily neměřitelně odlišnou kinetickou energii, jako teorie newtonovská.
Lokalizace chyb
Pokud při výpočtu dojde k chybě, jsme na to upozorněni. Pokud program spoštíme z příkazové řádky, je program ukončen.
Pokud pracujeme v interaktivním režimu a pokud dojde k chybě uvnitř nějaké funkce, je provádění kódu ukončeno na globální úrovni, tedy lokální proměnné volaných funkcí zmizí a nejsou dostupné. Globální proměnné zůstávají ve stavu v jakém se nacházely v okamžiku chyby.
Ilustrujme si to na následujcícím příkladu. Definujeme funkci
a poté zkusíme spočíst \(g(x,y) = f(x,-y,n)/f(x,y,n)\) pro \(y=1\) a dostatečně velké \(n\).
[ ]:
# demonstrace výpisu chyby
def f(x,y,n):
"""Demonstrace lokalizace chyb."""
s = 0.0
xk = x
for k in range(1,n+1):
s = s + xk/(k-y)
xk *= x
return s
def g(x,y):
p = f(x,-y,50)
q = f(x,+y,50)
return p/q
print(g(0.5,1))
Chybová hlášení závisejí na způsobu, jímž kód výše spustíme. Pro naše potřeby je nejsrozumitelnější hlášení v prostředí Jupyter:
---------------------------------------------------------------------------
ZeroDivisionError Traceback (most recent call last)
Cell In[1], line 18
15 q = f(x,+y,50)
16 return p/q
---> 18 print(g(0.5,1))
Cell In[1], line 15, in g(x, y)
13 def g(x,y):
14 p = f(x,-y,50)
---> 15 q = f(x,+y,50)
16 return p/q
Cell In[1], line 7, in f(x, y, n)
5 xk = x
6 for k in range(1,n+1):
----> 7 s = s + xk/(k-y)
8 xk *= x
10 return s
ZeroDivisionError: float division by zero
Na prvním řádku se dozvíme, že došlo k dělení nulou a že funkce, které byly volány naposledy, jsou uvedeny na konci výpisu. Hlášení sděluje, že v rámci příkazu print(g(0.5,1)) došlo chybě, protože při výpočtu q = f(x,+y,50) došlo ve funkci f k dělení nulou při vyhodnocení pravé strany přiřazovacícho příkazu s = s + xk/(k-y).
V našem případě je chyba zřejmá, v \(y=1\) není \(g(x,y)\) definována. V situacích, kdy nám chyba z kódu zřejmá není, musíme chybu hledat za běhu programu. Dva klíčové postupy jsou
Program domplníme o vhodné množství příkazů
print, které na obrazovku nebo do soboru pošlou dostatek informací o průběhu výpočtu, abychom z nich chybu dokázali najít. Pokud do funkcefpřidáme na začátek cyklu příkazprint(f'f({x},{y},{n}): pricitam {xk}/{(k-y)}')budou poslední dva řádky ladícího výstupu
f(0.5,-1,50): pricitam 8.881784197001252e-16/51
f(0.5,1,50): pricitam 0.5/0
Použijeme nástroje pro ladění dostupné v IDE jako je VS Code nebo PyCharm, kde se výpočet pozastaví ještě uvnitř funkce, kde k chybě došlo a máme možnost zkoumat atuální stav lokálních proměnných.
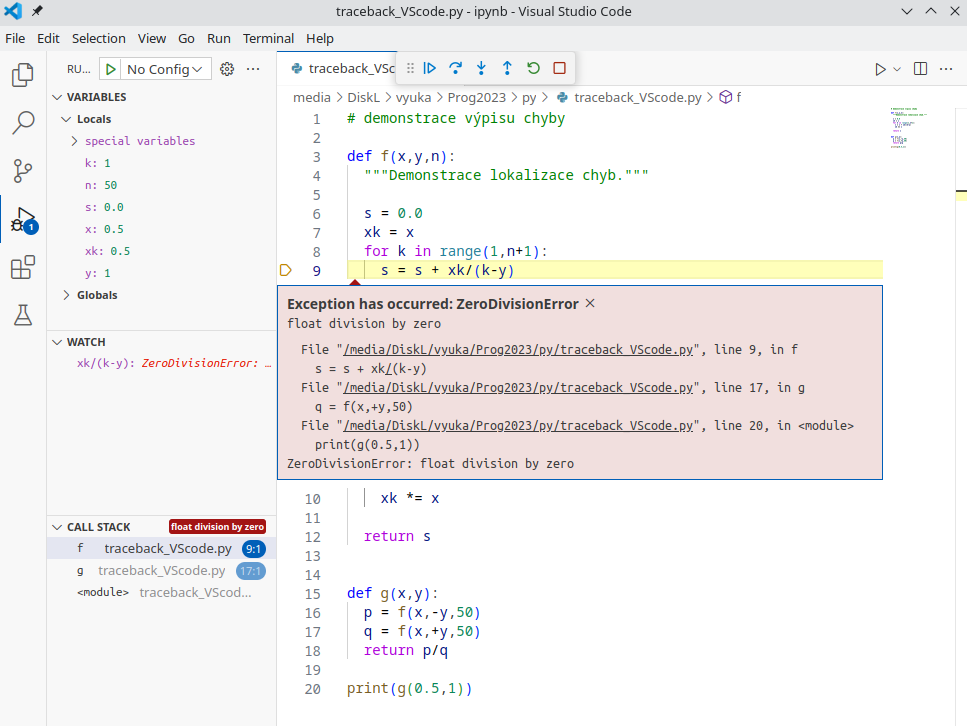
Obrázek: Snímek prostředí VS Code zachycující ohlášení dělení nulou. V levém sloupci dole je seznam funkcí zavolaných v okamžiku havárie, zde tedy, že g zavolala f. Pro funkci, kterou zde vybereme je nahoře dostupná informace o jejích lokálních proměnných. V prostřední části levého sloupce je možno přidat výraz, který nás zajímá. Zde vidíme, že pro aktuální hodnoty lokálních proměnných funkce f vede výraz xk/(k-y) k dělení nulou.
To, že program rozdělíme na funkce přináší při hledání chyb výhodu. Pokud identifikuje problematickou funkci, můžeme napsat samostatný kód, který ji separátně testuje. Je zřejmé, že takové testování se zkomplikuje, pokud problematická funkce komunikuje s jinými prostřednictvím globálních proměnných.
[ ]:
 Programování pro fyziky (1.r)
Programování pro fyziky (1.r) Obsah
Obsah