Řetězce II
Seznámili jsme se již s nejzákladnějšími operacemi s řetězci.
Vytvoření řetězce explicitním zápisem (literálem)
s = 'retezec v apostrofech'as = "retezec v uvozovkach"Vytvoření řetězce konverzí
s = str(math.pi)Vytvoření řetězce obsahujícího znak s daným ASCII/Unicode kódem
chr(65)
Také jsme potkali speciality
Speciální znaky
"a\tb\n1\t2"Formátované řetězce
f'Pro n={2**i} je vysledek {spoctiTo(i)}'Víceřádkové řetězce
s = '''\
<html>
<body>
<h1>Hola!</h1>
</body>
</html>
'''
Dále jsme viděli elementární operace s řetězci
Spojování
'a'+'b'(dá 'ab')Množení
'a'*5(dá 'aaaaa')
Řetězce vs. pole znaků
Je přirozené nahlížet na řetězce jako na pole znaků. Můžeme tedy použít složené závorky a z řetězce přečíst znak na dané pozici. První znak řetezce má index 0, druhý 1, atd.
[ ]:
s = 'ABCD'
for i in range(len(s)):
print(f's[{i}] == "{s[i]}"')
s[0] == "A"
s[1] == "B"
s[2] == "C"
s[3] == "D"
Abychom si procvičili práci s indexy u řetězců, napíšeme si nejprve funkci převádející řetězec na celé číslo. Samozřejmě, činíme tak jen z výukových důvodů, protože takovou službu již poskytuje konverze int(s), kde s je řetězec obsahující dekadický zápis čísla.
[ ]:
def atoi(s):
'převede řetězec na celé číslo'
i = 0 # index cifry
n = 0 # postupně se kumulující výsledek
for i in range(len(s)):
assert '0' <= s[i] <= '9', "Neplatná cifra"
n = n*10 + ord(s[i])-ord('0')
return n
def atoi2(s):
'převede řetězec na celé číslo, tato varianta funkce nepoužívá indexy'
i = 0 # index cifry
n = 0 # postupně se kumulující výsledek
for c in s:
assert '0' <= c <= '9', "Neplatná cifra"
n = n*10 + ord(c)-ord('0')
return n
print( atoi('123456') )
123456
Stejně jako u polí můžeme i u řetězců použíl řezy, tedy např.
[ ]:
s = 'ABCD'
print(f'{ s = }')
print(f'{ s[1:3] = }')
print(f'{ s[1:] = }')
print(f'{ s[:-1] = }')
s = 'ABCD'
s[1:3] = 'BC'
s[1:] = 'BCD'
s[:-1] = 'ABC'
Zajímavou pomůckou pro zapamatování je, že u řetězců (protože operace + znamená spojování) platí s[:n] + s[n:] == s pro libovolnou (i zápornou) hodnotu n.
To vše ale platí, pokud informaci z řetězce čteme. Není ale dovoleno modifikovat konkrétní znak. Řetězce (typ str) představuje totiž v logice jazyka Python immutable typ. Nebude nám to asi vadit, protože většinou budeme po možnosti modifikovat jednotlivé znaky řetězce toužit v situaci, kdy je cíle možno dosáhnout zavoláním některé z metod typu str.
Nejprve si zběžně ujasněme termín metoda. Souvisí s principy tzv. objektového přístupu k programování, my se zatím učíme přístup procedurální a tak lze zkráceně říci, že jde o funkci, jejíž první argument se místo do závorek za název (identifikátor) funkce nebo procedury připojuje před její název tečkou. Zatímco
len('111939')je příkladem volání funkce, kde řetězec je její argument a vrací celé číslo 6, tedy počet znaků, který tvoří daný řetězec'111939'.count('9')je příkladem volání metody. První argument sa nachází před tečkou a volání vrátí hodnotu 2, protože devítka je v řetězci \(2\times\).Pokud by se nám nelíbilo, že
countmusíme psát za tečku, můžeme defiovat stejnojmenou funkci dvou argumentůdef count(x, a): return x.count(a)
a poté psát např.
print( count('111223', '2') ).
Vybrané metody typu str.
Operací, které jsou takto dostupné jako metody typu str hodně. Podrobně vše najdete v dokumentaci, zde jen stručné shrnutí. Tyto funkce občas uvidíte použité v příkladech, ale je jasné, že jejich znalost nebude u zkoušky potřeba.
Mnoho funkcí se zabývá modifikací velkých a malých písmen v řetězci, např.
lower, upper, capitalize, swapcase. Příklad:'xxxxii'.upper() == 'XXXXII'.Další funkce testují, zda řetězec splňuje nějaká kritéria, např.
isalpha, isdecimal, islower.Odstranění mezer na začátku a/nebo konci řetězce zajistí metody
strip, lstrip, rstrip. Příklad:' 1 2 3 '.strip() == '1 2 3'.Metody
findareplacezajistí elementární vyhledávání a nahrazovanání v řetězci.print( '1\t2\t3'.replace('\t','...') )vytiskne
1...2...3
Většinou však použijete složitější variantu používajíc tzv. *regulární výrazy`, která dovolí pohodlně provét i takovou operaci, jako nalezení letopočtů zapsných v římskými číslicemi v textu a jejich nahrazení dekadickou hodnotou. Jde o rozsáhlé téma, které sice nespadá do "základů programování", nicméně je natolik důležité, že o existenci musíte vědět. Proto jej zmíníme v kapitole "Co jsme nestihli".
Podobné operaci hledání je rozdělení řetězce na seznam řetězců. Opět můžeme vzít jako oddělovač jediný znak (např. čárku), pak nám stačí metoda
splittypustr. Důležitý příklad souvisí s interpretací řádku čísel načtených ze souboru.
Příklad Následující kód nejprve získá data o hranicích souhvězdí z webu a následně je načte. Protože bez podpory dalších knihoven mámě v Pythonu načtená data v podobě řetězce musíme tento převést na číslené údaje.
Klíčová je zde funkce str.split(sep), která rozdělí řetězec na místech určených hodnotou argumentu sep. V našem případě je to jednak mezera a poté dvojtečka (viz formát dat).
Další užitečnou vlastností jazyka, kterou několikrát využijeme je unpacking.Již víme, že ten v nejjednodušší podobě znamená přiřazení prvků pole do tolika proměnných, kolik je délka pole, např. a,b,c = [1,2,3].
Pozn. Pokud program spouštíte na počítači, kde nemáte instalovaný program wget, soubor bound_edges_18.txt můžete do běžného adresáře uložit webovým prohlížečem.
[ ]:
# Hranice souhvězdí ze stránky https://pbarbier.com/constellations/boundaries.html
! wget https://pbarbier.com/constellations/bound_edges_18.txt
--2023-12-11 10:29:31-- https://pbarbier.com/constellations/bound_edges_18.txt
Resolving pbarbier.com (pbarbier.com)... 104.244.120.9
Connecting to pbarbier.com (pbarbier.com)|104.244.120.9|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 89114 (87K) [text/plain]
Saving to: 'bound_edges_18.txt'
bound_edges_18.txt 100%[===================>] 87.03K 487KB/s in 0.2s
2023-12-11 10:29:32 (487 KB/s) - 'bound_edges_18.txt' saved [89114/89114]
[ ]:
# Nakreslí lomené "čáry" vyznačující dané souhvězdí na obloze
# data v souboru mají formát/význam
#
# 587:586 P+ 11:31:00 +11:00:00 11:52:00 +11:00:00 VIR LEO
# KE1:KE2 ED RA1 DE1 RA2 DE2 CO1 CO2
#
# KE1,KE2 ... Vertex keys
# ED ... Edge type and direction -- [M]eridian or [P]arallel
# RA1, DE1 ... Right ascension and declination (B1875) of 1st vertex
# RA2, DE2 ... Right ascension and declination (B1875) of 2nd vertex
# CO1, CO2 ... Constellations delimeted by this edge
import matplotlib.pyplot as plt
def hex2dec(xms):
"Převádí úhel v šedesátkové (hexagesimální) soustavě x:minuty:vteřiny na reálné číslo"
x, m, s = xms.split(':')
return int(x) + int(m)/60 + int(s)/3600
def plot_constellation_bdry(name):
'Nakreslí lomenou "čáru" vyznačující dané souhvězdí na obloze'
hrs2deg = -360/24 # konverze hodin na stupně u rektascense
with open('bound_edges_18.txt') as file:
for line in file:
ke12, ed, ra1, de1, ra2, de2, co1, co2 = line.split(' ')
if co1==name or co2==name:
ra1 = hex2dec(ra1) * hrs2deg
de1 = hex2dec(de1)
ra2 = hex2dec(ra2) * hrs2deg
de2 = hex2dec(de2)
plt.plot([ra1,ra2],[de1,de2],'k')
plot_constellation_bdry('ORI')
plt.axis("equal")
plt.grid()
plt.show()
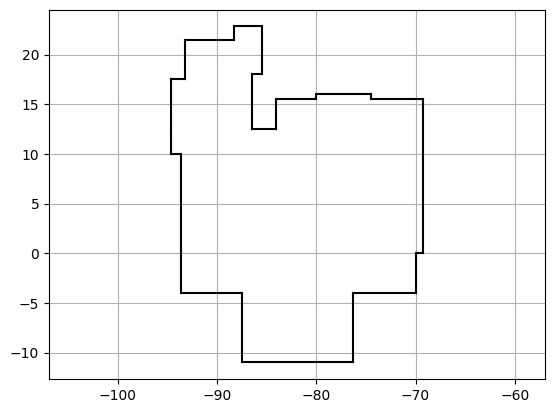
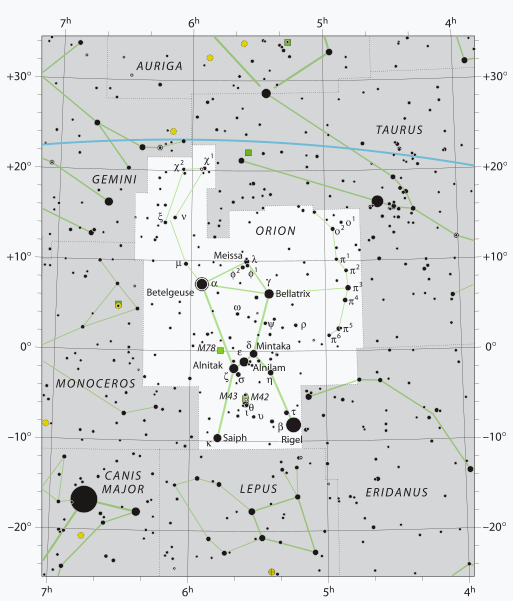
Srovnáním našeho obrázku s tím na wikipedii vidíme nedostaky našeho zobrazení sféry na rovinu (naše poledníky jsou vertikály). Orientace a škálování vodorovné osy na tomto obrázku pak vyjasní, proč jsem museli použít konstantu hrs2deg = -360/24.
 .
.
Regulární výrazy
Jde o jazyk určený k popisu řetězců. Například má-li být identifikátor neprázdná posloupnost písmen, číslic a podtržítka nezačínající číslicí, použijeme regulární výraz
[a-zA-Z_][a-zA-Z0-9_]*
Dnes se běžně používá v textových editorech ke specifikaci hledaného řetězce a pokud v programu potřebujeme upravovat řetězce (například při načítání dat v nepohodlném tvaru) je regulární výraz ve většině případů správným nástrojem jaký použít.
Pravidel pro psaní regulárních výrazů je hodně, ty nejdůležitější jsou - a znamená znak a - [abc] znamená znak a nebo b nebo c - [a-d] znamená znak a nebo b nebo c nebo d - [^xy] znamená libovolný znak kromě x a y - ab* znamená a nebo ab nebo abb nebo abbb atd. - ab+ znamená ab nebo abb nebo abbb atd. - ab? znamená a nebo ab - a(bb)?c znamená ac nebo abbc
Závorky navíc označují skupiny, jejichž hodnotu můžeme dále použít.
Regulární výrazy jsou dnes součástí nástrojů pro vyhledávání v editorech a jsou také vhodným nástrojem, pokud ve vašem programu potřebujete modifikovat řetězce nebo textové soubory. Následující příklad se pokouší řešit převod desetinné čárky v číslech na desetinnou tečku. Funkce re.sub (sub jako substitute) je zde použita se třemi parametry:
první představuje vyhledávaný text popsaný regulárním výrazem
druhý pak text, který jej má nahradit. Speciální výrazy
\1a\2se nahradí tím, co se napasovalo na první resp. druhou skupinu uvedenou v závorkách v regulárním výraze.třetí argument představuje prohledávaný text.
[1]:
import re
vstup = """\
1,23, 5,23, 7,02
16,365, 5,96, 11,32
"""
vystup = re.sub(r"([0-9]+),([0-9]+)",r"\1.\2", vstup)
print(vystup)
1.23, 5.23, 7.02
16.365, 5.96, 11.32
Poznámka: Na webu regexr.com si můžete vyzkoušet svoje nebo prohlédnout cizí nápady na tvar regulárního výrazu pro daný problém.
Cvičení: Zkuste vzít prvních pár řádek tabulky https://github.com/dbwebb-se/vlinux/blob/master/example/grep/presidents.txt a s použijtím výrazu ([A-Z])[a-z]+ (([A-Z])[a-z]+ )?([A-Z][a-z]+) upravte program výše, aby převáděl jména na iniciály: George Washington, 1789-1797 --> G. Washington, 1789-1797
 Programování pro fyziky (1.r)
Programování pro fyziky (1.r) Obsah
Obsah