Vybrané numerické algoritmy
Naše přednáška není přednáškou o numerických metodách. Přesto jsou zde pravidelně zmiňovány, protože
Základy programování pro fyziky
musejí přiblížit základy programování na nějakých úlohách. Algoritmy použité v numerických metodách jsou často z hlediska informatiky velice jednoduché a tedy vhodné na programování v úvodním kurzu.
by měly připravit posluchače na problémy, jaké v rámci programování fyzikové potkají. Mezi ně patří právě základní numerické algoritmy.
Přehled doposud probraných numerických témat
Hledání největšího společného dělitele (Euklidův algoritmus s odečítáním a pak s operací modulo)
Aritmetické výrazy
Volání knihovních funkcí (knihovny
mathascipy.special)Polynomy a Hornerovo schéma
Vyčíslení sum, součinů
Funkce definované rekurzivní formulkou
Hledání kořene (půlení intervalu, Newtonova metoda)
Důsledky zaokrouhlovacích chyb, reprezentace reálných čísel v počítači
Eratosthenovo síto
Organizace dat do polí
Hromadné vyčíslování skrze univerzální funkce v
numpyNumerická kvadratura (výpočet určitého integrálu lichoběžníkovým pravidlem, ostatní jen jako zajímavost)
Metoda Monte Carlo na příkladu numerické kvadratury
Vektory, matice, operace dot (
@)Řešení soustavy lineárních algebraických rovnic (jen Gaussova-Jordanova eliminace a volání
numpy.linalg.solve)
Zbývá ale ještě několik důležitých témat doplnit.
Polynomiální interpolace
Uvažujme, že nějaká veličina \(y\) závisí na hodnotě parametru \(x\). Je tedy rozumné mluvit o funkci \(y(x)\). Někdy ale může být výpočet funkce velmi náročný, a tak máme možnost ji zjistit jen v omezeném množství hodnot \(x\), jindy toto omezení vyplývá z toho, že funkce byla určena experimentálně pro omezené množství hodnot \(x\).
Předpokládejme, že z těchto důvodů známe její funkční hodnoty jen ve vybraných bodech \(x_1 < x_2 < ... < x_n\). Nastává otázka, co můžeme říci o hodnotě funkce \(y\) v nějakém bodě \(x\), kde
\(x_1<x<x_n\). Pak mluvíme o interpolaci.
\(x<x_1\) nebo \(x>x_n\). Pak mluvíme o extrapolaci.
Jde o složitou otázku, nás bude zajímat jen varianta, kdy budeme zkoumat polynom, který v uvedených bodech nabývá stejnou hodnotu. Pokud je jeho řád \(n-1\), pak je určen jednoznačně.
Interpolace jako příklad užití knihovní funkce
Následující kód používá knihovní funkci scipy.interpolate.lagrange. Ta vrátí funkci, které když dáme argument, spočte jeho hodnotu.
[51]:
from scipy.interpolate import lagrange
import math
import numpy as np
import matplotlib.pyplot as plt
f = np.arctan
a, b = -3, 3
nc_list = [(4, 'red'), (8, 'blue'), (12, 'green')]
dx = (b-a)/64
x_plot = np.linspace(a-dx,b+dx,200)
plt.plot( x_plot, f(x_plot) , color='gray', linewidth=0.4)
for n, c in nc_list:
x = np.linspace(a, b, n)
y = f(x)
poly = lagrange(x, y)
plt.plot( x_plot, poly(x_plot), color=c)
plt.plot( x, y, 'o', color=c)
plt.title('Polynomiální interpolace')
plt.grid()
plt.show()
for n, c in nc_list:
x = np.linspace(a, b, n)
y = f(x)
poly = lagrange(x, y)
plt.plot( x_plot, poly(x_plot)-f(x_plot), color=c)
plt.plot( x, np.zeros_like(x), 'o', color=c)
plt.title('Chyba polynomiální interpolace')
plt.grid()
plt.show()
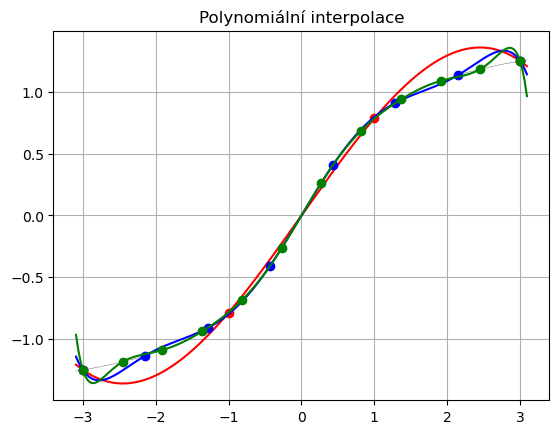
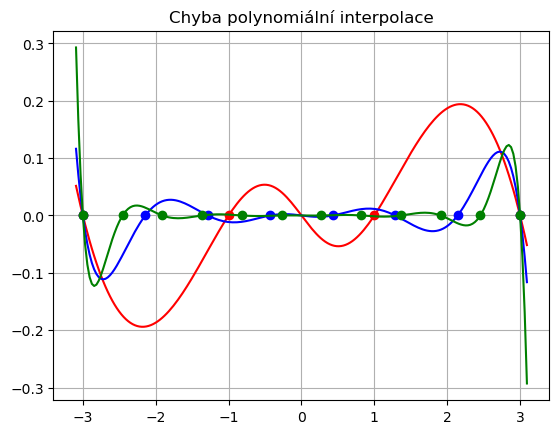
Cvičení: pozorujte, jak se chování interpolačního polynomu liší
když zkracujete délku intervalu,
když funkci \(\arctan\) nahradíte \(\exp\).
když místo ekvidistantního vzorkování (které dá
np.linspace(a, b, n)) použijete níže uvedené hodnoty \(x_i\) podle Čebyševa.
Lagrangeova interpolace je založena na faktu, že funkci můžeme např. pro \(n=4\) rozložit na součet
členů tvaru
což je polynom, který v je nulový ve všech bodech \(x_i\) s výjimkou \(x_2\), kde nabývá hodnoty \(y_2\).
Proto má výsledný vzorec tvar
neboli
[53]:
import numpy as np
import matplotlib.pyplot as plt
def linterp(t, x, y):
n = len(x)
assert len(y) == n
s = 0.0
for i in range(n):
p = y[i]
for j in range(n):
if i!=j:
p *= (t-x[j])/(x[i]-x[j])
s += p
return s
f = np.arctan
a, b = -3, 3
nc_list = [(4, 'red'), (8, 'blue'), (12, 'green')]
dx = (b-a)/64
x_plot = np.linspace(a-dx,b+dx,200)
plt.plot( x_plot, f(x_plot) , color='gray', linewidth=0.4)
for n, c in nc_list:
x = np.linspace(a, b, n)
y = f(x)
y_plot = [linterp(t, x, y) for t in x_plot]
plt.plot( x_plot, y_plot, color=c)
plt.plot( x, y, 'o', color=c)
plt.title('Polynomiální interpolace')
plt.grid()
plt.show()
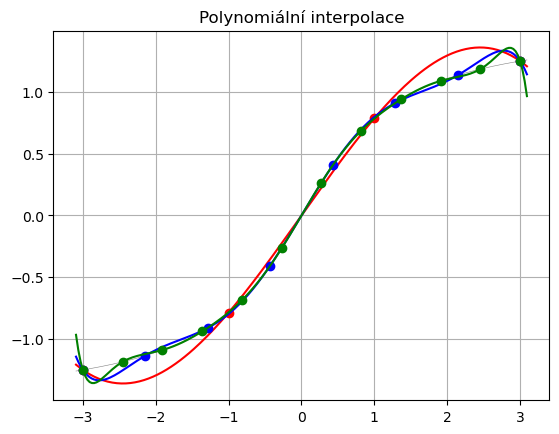
Ukazuje se, že pro větší počet bodů, skrz které interpolační polynom prokládáme, je ekvidistantní vzorkování nevhodné. Mnohem lepšího souladu mezi interpolovanou funkcí a její aproximací lze dosáhnout, pokud
použijeme nerovnoměrné vzorkování intervalu, např. podle Čebyševa,
\[x_i = \frac{a+b}{2} + t_i \frac{b-a}{2}, \;\;\; t_i = \cos \pi \frac{ n - k - \tfrac12}{n},~~~ i = 0, 1, .. n - 1\]interval rozdělíme na více částí a opakovaně použijme polynomiální interpolaci skrze menší počet bodů. Metoda, která se jednotlivé úseky snaží hladce navázat, se jmenuje spline (viz ukázka použití
CubicSplineníže).
Obojí si můžete vyzkoušet jako cvičení na práci s poli a vést v patrnosti, že se máte podívat do příslušné učebnice, kdybyste potřebovali polynomiální interpolaci větším počtem bodů.
[65]:
from scipy.interpolate import lagrange, CubicSpline
import math
import numpy as np
import matplotlib.pyplot as plt
f = np.arctan
a, b = -3, 3
dx = (b-a)/64
x_plot = np.linspace(a-dx,b+dx,200)
plt.plot( x_plot, f(x_plot) , color='gray', linewidth=0.4)
n = 8
x = np.linspace(a, b, n)
y = f(x)
poly = lagrange(x, y)
spline = CubicSpline(x,y)
plt.plot( x_plot, poly(x_plot), label='Lagrange')
plt.plot( x_plot, spline(x_plot), '--', label='cubic spline')
plt.plot( x, y, 'o')
plt.title('Polynomiální vs. splajnová interpolace')
plt.grid()
plt.legend()
plt.show()
x = np.linspace(a, b, n)
y = f(x)
poly = lagrange(x, y)
spline = CubicSpline(x,y)
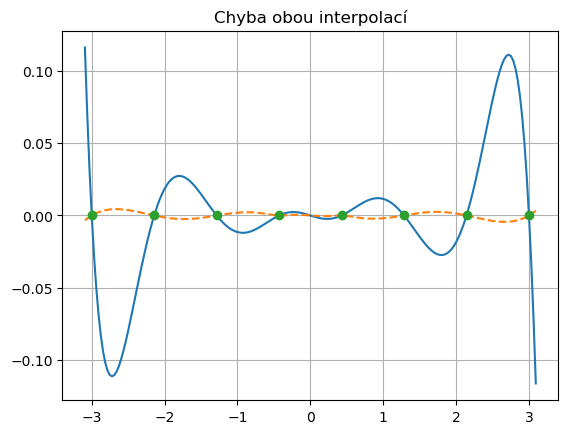
plt.plot( x_plot, poly(x_plot)-f(x_plot))
plt.plot( x_plot, spline(x_plot)-f(x_plot), '--')
plt.plot( x, np.zeros_like(x), 'o')
plt.title('Chyba obou interpolací')
plt.grid()
plt.show()
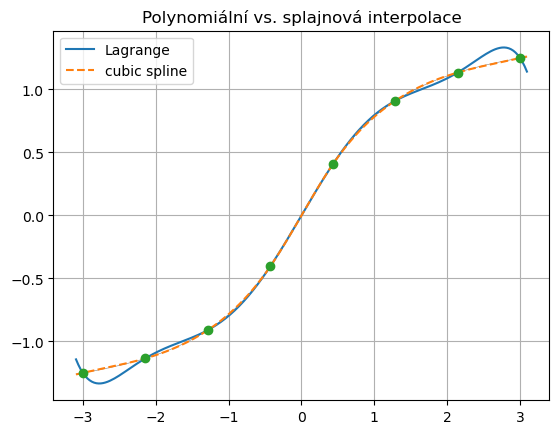
Polynomiální regrese
Často nepožadujeme, aby daná křivka určenými body procházela přesně, ale aby minimalizovala vhodně definovanou chybu. Nejsnazší je tzv. metoda nejmenších čtverců, kde máme lineární model
závisející na \(m<n\) parametrech \(p_A\) určujících souřadnice v bázi funkcí \(f_A(x)\) a uvažovat chybu v podobě kvadratického výrazu
kde \(\cal F_{iA}\) je obdélníková matice hodnot \(A\)-té bázové funkce v \(i\)-tém bodě.
Schematicky můžeme psát, že od minimalizace chyby požadujeme
kde ale dimenze vektorů \({\rm dim}\;\vec y > {\rm dim}\; \vec p\), v případě požadování rovnosti by tedy šlo o přeurčenou soustavu lineárních rovnic.
My umíme řešit soustavy rovnic se čtvercovou maticí a je zajímavé, že minimalizace kvadratického výrazu dá lineární soustavu rovnic pro \(\vec p\), která z té předchozí vnikne vynásobemím transponovanou maticí \(\cal F^T\)
V rámci našeho předmětu nemusíme rozumět původu rovnic, ale musíme je umět převést do kódu. Proto následuje ukázka programu odpovídajícího na otázku, jaký polynom třetího stupně minimalizuje sumu kvadrátu odchylek od průběhu funkce sinus pro sadu \(n\) rovnoměrně rozložených bodů na intervalu \(<\!\!0,\pi/2\!\!>\).
Kód ukazuje dvě varianty. Jedna sestavuje výše uvedenou matici a řeší soustavu rovnic, druhá volá numpy.polyfit.
[85]:
import numpy as np
n = 17
x_samples = np.linspace(0,np.pi/2, n)
y_samples = np.sin(x_samples)
# varianta 1 ... sestavme matici, řešme soustavu
def basis(x):
return np.array([x*x*x, x*x, x, 1])
matrix_F = np.array( [basis(x) for x in x_samples] )
matrix_FT = matrix_F.transpose()
coeffs1 = np.linalg.solve( matrix_FT @ matrix_F , matrix_FT @ y_samples)
print( coeffs1 )
# varianta 2 ... použijme numpy
coeffs2 = np.polyfit(x_samples, y_samples, 3)
print( coeffs2 )
[-0.11347006 -0.06919881 1.02515468 -0.00154229]
[-0.11347006 -0.06919881 1.02515468 -0.00154229]
Cvičení: Nakreslete graf funkce \(\sin x\) a polynomu nalezeného regresí.
Cvičení: V principu lze matici F vytvořit příkazem matrix_F = basis(x_samples).transpose() Zkuste to! (Nápověda: Ještě je potřeba mírně upravit kód funkce basis, protože, zatímco x*x*x i x*x jsou vektory stejně jako x, výraz 1 je skalár.)
Optimalizace (jako příklad použití knihovního algoritmu)
Hledání minima (nebo maxima) nějaké funkce je velmi složitým problémem. Jedním z důvodů je, že minimalizovaný výraz může mít mnoho lokálních minim, "údolí" v jejich okolí také mohou mít ve více proměnných ošklivý tvar. Existuje proto velké množství přístupů k numerickému hledání extrému funkce více proměnných, nás teď bude zajímat, jak pro již hotový algoritmus náš konkrétní problém upravit.
Vezmeme minulou úlohu, ale místo nejmenších čtverců zvolíme jako míru příhodnosti aproximace maximální nalezenou odchylku. Rázem jde o nelineární problém. Abychom jej mohli knihovní funkci scipy.optimize.minimize předložit:
musíme prozkoumat dokumentaci, ze které nahlédneme, že funkce má mnoho parametrů, ale jen dva povinné:
jakou funkci chceme minimalizovat, tato funkce má jeden argument s významem pole parametrů,
počáteční odhad hodnoty parametrů. Ten kromě informace, kde začít hledat (což i u našeho jednoduchého problému může ovlivnit, které minimum funkce najde), dává funkci `minimize`` informaci o tom, kolik neznámých parametrů má hledat. My začneme s hodnotami nalezenými metodou nejmenších čtverců.
Dále z dokumentace zjistíme, že funkce vrací hodnotu nalezených parametrů v atributu
x, to zda se povedlo nal0zt minimum v atributusuccessa chybové hlášení v atributumessage.musíme napsat funkci
maxdev(c), která vrací \(\max_{i} |f(x_i)-\sin x_i|\), kde \(f(x)=\sum_{i=0}^3 c_i x^i\).musíme zavolat funkci
scipy.optimize.minimizes oběma výše uvedenými argumenty.minimalizace může z mnoha důvodů havarovat (v našem příkladě stačí vzít jiné \(n\)), proto použijeme
assertnakonec je potřeba z vráceného výsledku extrahovat koeficienty
Neodpustím si komentář, že uvedený postup jak získat polynomickou aproximaci funkce, je především demonstrací hledání minima funkce více proměnných, nikoli optimálním přístupem.
[88]:
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
# zadání problému: optimální aproximace sin(x) minimalizující max |chyby|
n = 27
x_samples = np.linspace(0,np.pi/2, n)
y_samples = np.sin(x_samples)
def poly_eval(coeffs, x):
"Hodnota polynomu 3.stupně v x, kde x může být np.ndarray"
return ((coeffs[0]*x + coeffs[1])*x + coeffs[2])*x + coeffs[3]
def maxdev(coeffs):
"maximum odchyky polynomu(x) a sin(x)"
return max(abs(y_samples - poly_eval(coeffs, x_samples)))
# nejprve chi^2
coeffs2 = np.polyfit(x_samples, y_samples, 3)
print( ' chi^2 coeffs =', coeffs2 )
# zkusíme minimalizaci
res = minimize(maxdev, coeffs2)
assert res.success, res.message
coeffs3 = res.x
print( 'minimize coeffs =', coeffs3 )
# vypíšeme maximální chybu
print( 'minimize error =', maxdev(coeffs3) )
print( ' chi^2 error =', maxdev(coeffs2) )
# namalujeme grafy chyb
x_plot = np.linspace(0,np.pi/2,200)
y_plot = np.sin(x_plot)
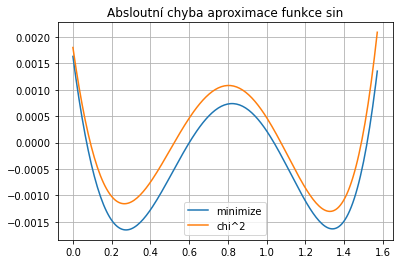
plt.plot( x_plot, y_plot - poly_eval(coeffs3, x_plot), label='minimize')
plt.plot( x_plot, y_plot - poly_eval(coeffs2, x_plot), label='chi^2')
plt.legend()
plt.grid()
plt.title('Absloutní chyba aproximace funkce sin')
plt.show()
chi^2 coeffs = [-0.11360154 -0.0694899 1.02589085 -0.00179986]
minimize coeffs = [-0.11203843 -0.073022 1.02794336 -0.00163133]
minimize error = 0.0016313314926229042
chi^2 error = 0.002088831061687557
Numerické derivování
Někdy se stane, že potřebujeme spočíst derivaci funkce, jejíž hodnoty známe jen číselně. Ukazuje se, že jde o těžký problém, protože např. v definičním vzorečku
se nepíše, jak moc malé máme vzít \(\epsilon\) abychom dostali hodnotu derivace s rozumnou přesností. Jedna potíž spočívá v tom, že pokud vezmeme \(\epsilon\) opravdu hodně malé, bude mít \(x+\epsilon\) v důsledku zaokrouhlení v rámci typu float stejnou hodnotu jako \(x\), a tedy vyjde derivace nulová.
Ukazuje se, že vzorec
dovoluje použít větší \(\epsilon\) a získat tak výsledek méně zatížený zaokrouhlováním.
Opět, v našem kurzu se především učíme umět napsat kód, ten následující porovná, jak je to s chybami obou vzorců. Funkční hodnoty \(x_i = x_0+i \epsilon\) a \(y_i = f(x_i)\) budeme mít uloženy v poli. Protože jde o ekvidistantní vzorkování, můžeme při odečítání sousedních prvků podle vzorců výše výhodně použít řezy polí. Abychom nemuseli řešit derivování u kraje pole, hodnoty derivací v krajních bodech nepočítáme.
[110]:
import numpy as np
n = 25
xi = np.linspace(-1,1,n)
yi = np.exp(xi)
dy = yi[1:-1] # exp'(x) = exp(x)
epsilon = xi[1]-xi[0]
dy1 = (yi[2:]-yi[1:-1])/epsilon
dy2 = (yi[2:]-yi[0:-2])/(2*epsilon)
err1 = max( abs( dy1-dy ))
err2 = max( abs( dy2-dy ))
print('Chyby vzorců pro numerickou derivaci:')
print(f'{err1 = :6.2g} {err2 = :6.2g}')
Chyby vzorců pro numerickou derivaci:
err1 = 0.11 err2 = 0.0029
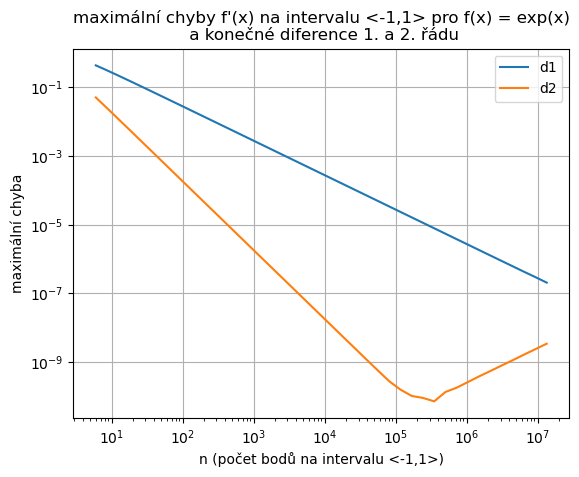
Obrázek níže ilustruje, že ani pro optimální \(\epsilon\) se druhý vzoreček nepřiblíží přesnosti, na kterou jsme zvyklí, když vyčíslujeme matematické funkce. Numerické derivování není snadné.
Cvičení: Ignorujte kód níže a napište nějaký svůj, který vyrobí podobný obrázek.
[106]:
import matplotlib.pyplot as plt
def errs(n):
xi = np.linspace(-1,1,n)
yi = np.exp(xi)
dy = yi[1:-1] # exp'(x) = exp(x)
epsilon = xi[1]-xi[0]
dy1 = (yi[2:]-yi[1:-1])/epsilon
dy2 = (yi[2:]-yi[0:-2])/(2*epsilon)
err1 = max( abs( dy1-dy ))
err2 = max( abs( dy2-dy ))
return np.array([err1,err2])
nn = (1.2**np.linspace(10,90,41)).astype(int)
ww = np.array([errs(n) for n in nn])
plt.yscale('log') # logaritmický průběh os
plt.xscale('log')
plt.xlabel('n (počet bodů na intervalu <-1,1>)')
plt.ylabel('maximální chyba')
plt.title("maximální chyby f'(x) na intervalu <-1,1> pro f(x) = exp(x)\n a konečné diference 1. a 2. řádu")
plt.grid()
plt.plot(nn,ww[:,0],label='d1')
plt.plot(nn,ww[:,1],label='d2')
plt.legend() # zobraz popisek daný "label=..."
plt.show()
Řešení obyčejných diferenciálních rovnic
Od časů Newtona je mnoho problémů fyziky popisováno diferenciálními rovnicemi.
Nejprve uvažme následující kód. Realizuje tzv. Eulerovu metodu založenou na jednoduché nahrazení derivace
tedy konkrétně
Tento recept se používá opakovaně a pokud \(\Delta t\) neměníme, získáme ekvidistantně navzorkovaný odhad řešení diferenciální rovnice. Z hlediska programování jde tedy o jeden cyklus a sadu proměnných udržujících zejména informaci o hodnotách \(t_i, y_i\).
Program, který řeší rovnici \(dy/dy=-y\) s počáteční podmínkou \(y(0)=1\) je níže. Proč jsme jej již nepotkali na začátku kurzu souvisí se zpracováním získaných hodnot \(y_i\). Zde z nich budujeme seznam a ten pak vykreslíme.
[111]:
import math
steps_per_print = 100
dt = 0.1/steps_per_print
t_max = 1
n = 0
t = 0 # před cyklem jako obvykle nezapomeneme na inicializaci
y = 1 # zde má navíc význam počátečních podmínek
while t <= t_max + dt/2:
if n % steps_per_print == 0:
print(f'{t:6.4f} {y:6.4f} {math.exp(-t):6.4f}')
dydt = -y
y = y + dydt * dt
t = t + dt
n = n + 1
0.0000 1.0000 1.0000
0.1000 0.9048 0.9048
0.2000 0.8186 0.8187
0.3000 0.7407 0.7408
0.4000 0.6702 0.6703
0.5000 0.6064 0.6065
0.6000 0.5486 0.5488
0.7000 0.4964 0.4966
0.8000 0.4491 0.4493
0.9000 0.4064 0.4066
1.0000 0.3677 0.3679
Povšimněte si, že
počáteční podmínky pro diferenciální rovnici se v programu objevá jako inicializace proměnné
yv cyklu se pak opkovaně ze staré hodnoty
yspočte nová. Místo hodnot funkce uložené například v tabulce se tak řešení v programu objeví v jediné proměnné rozloženě v čase - v každém opakování cyklu jedna hodnota. Takový postup se nazývá "pochodový" algoritmus, nemusí složitě řešit uložení hodnot funkce a vystačí s minimem proměnných.když zmenšíme krok, což zde obstarává konstanta
steps_per_print, dostaneme přesnější výsledek. Snadno se lze přesvědčit, že pro desetkrát kratší krok bude chyba konečné hodnoty \(y(1)\) desetkrát menší.
Tento jednoduchý program jsme mohli napsat hned na první hodině a rozuměli bychom mu. Podobné úlohy řešily i první počítače, jejich stavitelé a programátoři ovšem věděli, že musejí použít numerickou metodu lepší než tu Eulerovu.
O něco komplikovanější kód nám dnes řešení i namaluje:
[125]:
import numpy as np
import matplotlib.pyplot as plt
steps_per_plot = 1
dt = 0.1/steps_per_plot
t_max = 3
t_data = []
y_data = []
n = 0
t = 0 # před cyklem jako obvykle nezapomeneme na inicializaci
y = 1 # zde má navíc význam počátečních podmínek
while t < t_max:
if n % steps_per_plot == 0:
t_data.append(t)
y_data.append(y)
dydt = -y
y = y + dydt * dt
t = t + dt
n = n + 1
y_presna = np.exp(-np.array(t_data))
plt.plot(t_data, y_data)
plt.plot(t_data,y_presna)
plt.grid()
plt.ylim(-0.05,1.05)
plt.show()
print(f'Maximální chyba y(t) = {max(abs(y_data-y_presna)):5.2g}')
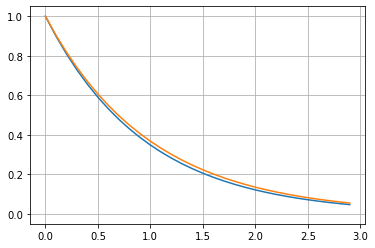
Maximální chyba y(t) = 0.019
Dále si ukážeme, že Newtonovy pohybové rovnice \(m\vec{\ddot x}=\vec F/m\) lze také zapsat jako diferenciální rovnici pro vektorovou veličinu \(\vec U\), jejíž polovina složek jsou polohy a druhá polovina rychlosti
Protože chceme mít po ruce kód, který řeší rovnice pro libovolnou podobu síly, kód přeuspořádáme. Protože v každém kroku numerického řešení diferenciální rovnice nabývá nové hodnoty jednak \(\vec U\) ale také \(t\), vrací funkce krok_Euler dvojici obou nových hodnot. Zatímco by bylo možné pozměnit argument U (je to pole, tedy je mutable), čas \(t\) je uložen v reálné proměnné (typ float je immutable) a proměnnou použitou jako aktuální argument pozměnit z vnitřku funkce
nelze.
[157]:
import math
import numpy as np
import matplotlib.pyplot as plt
def krok_Euler(t, U, fce_dUdt, dt):
"""
Jeden krok Eulerovy metody. Vrací dvojici nové_t, nové_U.
Argumenty:
U ......... výchozí hodnota U(t) (musí být typu numpy.ndarray)
fce_dUdt .. pravá strana dif. rovnice. Argumenty jsou t,U.
"""
prava_strana = fce_dUdt(t,U)
U = U + dt*prava_strana
t = t+dt
return t, U
def pohybova_rovnice_planety(t, U):
"Předpokládá U = [x,y,vx,vy]. Vrací časovou derovaci dle Newtona."
GM = 4 * math.pi**2 # grav. konstanta v jednotkách AU, rok, hmotnost_Slunce
x, y, vx, vy = U
r2 = x*x+y*y
r_3 = 1/(r2*math.sqrt(r2))
ax = - GM * x*r_3
ay = - GM * y*r_3
return np.array([vx, vy, ax, ay])
x_data = []
y_data = []
dt = 1/365/24/12 # 5 minut (ani tak nebude s Eulerovou metodou vysledek prilis presny)
tmax = 2 # dva roky
x0 = 0.5 # jednotka délky je AU
y0 = 0
vx0 = 0 # jednotka délky je AU/rok
vy0 = 2*np.pi # kruhová rychlost pro r=1AU
t = 0
Y = np.array([x0, y0, vx0, vy0])
while t<tmax:
x_data.append(Y[0])
y_data.append(Y[1])
t, Y = krok_Euler( t, Y, pohybova_rovnice_planety, dt);
plot_step = len(x_data)//1000+1
plt.plot(x_data[::plot_step], y_data[::plot_step])
plt.plot([0],[0],'or')
plt.axis('equal')
plt.grid()
plt.show()
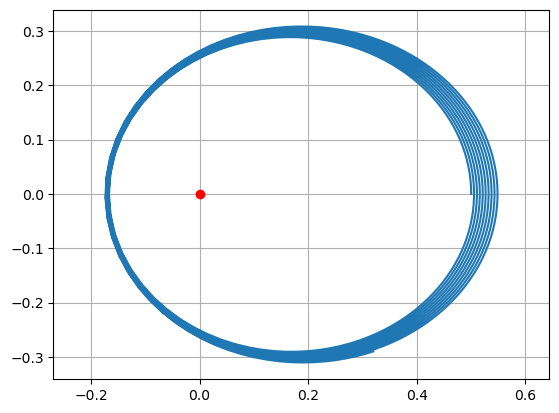
Toto rozdělení na rovnici pohybova_rovnice_planety a numerickou metodu krok_Euler je užitečné proto, že nyní můžeme (i bez pochopení detailů) nahradit Eulerovu metodu metodou lepší (u pohybu planety se to projeví potlačením deformace její eliptické orbity).
Pozn. Povšimněte si řádku
x, y, vx, vy = U
Již víme, že ten využívá vlastnosti přiřazení (nazývané unpacking), kdy obsah pole nebo seznamu o čtyřech položkách přiřadíme do čtyřech proměnných. Zatímco např. v metodě krok_Euler je totiž výhodné pracovat s polem naráz, abychom např. mohli využít sčítání vektorů, ve funkci pohybova_rovnice_planety se projeví, že každá položka pole má jiný význam a vhodné pojmenování prvků pole zpřehlední kód.
[155]:
import math
import numpy as np
import matplotlib.pyplot as plt
def krok_midpoint(t, U, fce_dUdt, dt):
"""
Jeden krok Eulerovy metody. Vrací dvojici nové_t, nové_U.
Argumenty:
U ......... výchozí hodnota U(t) (musí být typu numpy.ndarray)
fce_dUdt .. pravá strana dif. rovnice. Argumenty jsou t,U.
"""
prava_strana = fce_dUdt(t,U)
Umid = U + dt*0.5*prava_strana
prava_strana = fce_dUdt(t+dt*0.5,Umid)
U = U + dt*prava_strana
t = t+dt
return t, U
def pohybova_rovnice_planety(t, U):
"Předpokládá U = [x,y,vx,vy]. Vrací časovou derovaci dle Newtona."
GM = 4 * math.pi**2 # grav. konstanta v jednotkách AU, rok, hmotnost_Slunce
x, y, vx, vy = U
r2 = x*x+y*y
r_3 = 1/(r2*math.sqrt(r2))
ax = - GM * x*r_3
ay = - GM * y*r_3
return np.array([vx, vy, ax, ay])
x_data = []
y_data = []
dt = 1/365/24 # jedna hodina
tmax = 2 # dva roky
x0 = 0.5 # jednotka délky je AU
y0 = 0
vx0 = 0 # jednotka délky je AU/rok
vy0 = 2*np.pi # kruhová rychlost pro r=1AU
t = 0
Y = np.array([x0, y0, vx0, vy0])
while t<tmax:
x_data.append(Y[0])
y_data.append(Y[1])
t, Y = krok_midpoint( t, Y, pohybova_rovnice_planety, dt);
plot_step = len(x_data)//1000+1
plt.plot(x_data[::plot_step], y_data[::plot_step])
plt.plot([0],[0],'or')
plt.axis('equal')
plt.grid()
plt.show()
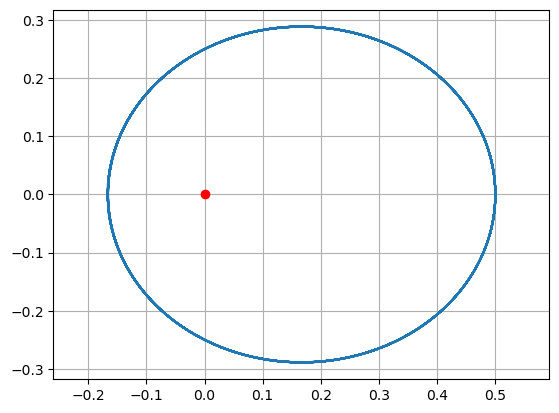
Teď, když rozumíme principu řešení diferenciálních rovnic s počáteční podmínkou (initial-value problem, IVP), můžeme náš postup porovnat s řešením prostřednictvím knihovní funkce scipy.integrate.solve_ivp. Použijeme volání
sol = solve_ivp(pohybova_rovnice_planety, (0,tmax), U0, max_step=dt)
První argument určuje řešenou diferenciální rovnici. Jde o stejnou funkci jako v předchozích příkladech.
Druhý argument má podobu intervalu proměnné \(t\), na kterém numerické řešení hledáme. To znamená, že funkce
solve_ivpvrátí pole hodnot pokrývajících tento interval.Dále musíme zadat počáteční podmínky. K tomu slouží třetí argument.
Jako obvykle má knihovní funkce několik nepovinných parametrů, my použijeme jediný,
max_step, kterým si vynutíme zkrácení kroku na vhodnou hodnotu. K tomu můžeme mít dva důvody. Jednak tím snížíme chybu, můžeme ale takto také donutitsolve_ivp, aby vrátil dostatečně hustě navzorkované řešení např. pro jeho vykreslení - při velkém kroku by se lomená čára znatelně odlišovala od křivky i když by procházela správnými body.
Příkaz plt.plot(sol.y[0], sol.y[1]) ukazuje, že vrácená hodnota sol má řešení uložené jako pole sol.y s dvěma indexy. První index určuje jednu z funkcí \(x(t), y(t), v_x(t), v_y(t)\). Druhý index pak konkrétní vzorek.
[103]:
from scipy.integrate import solve_ivp
import numpy as np
import math
def pohybova_rovnice_planety(t, U):
"Předpokládá U = [x,y,vx,vy]. Vrací časovou derovaci dle Newtona."
GM = 4 * math.pi**2 # pro grav. konstantu v jednotkách AU, rok, hmotnost_Slunce
x, y, vx, vy = U
r2 = x*x+y*y
r_3 = 1/(r2*math.sqrt(r2))
ax = - GM * x*r_3
ay = - GM * y*r_3
return np.array([vx, vy, ax, ay])
dt = 1/365 # jeden den
tmax = 2 # dva roky
x0 = 0.5 # jednotka délky je AU
y0 = 0
vx0 = 0 # jednotka délky je AU/rok
vy0 = 2*np.pi # kruhová rychlost pro r=1AU
U0 = np.array([x0, y0, vx0, vy0])
sol = solve_ivp(pohybova_rovnice_planety, (0,tmax), U0, max_step=dt)
plt.plot(sol.y[0], sol.y[1])
plt.plot([0],[0],'or')
plt.axis('equal')
plt.grid()
plt.show()
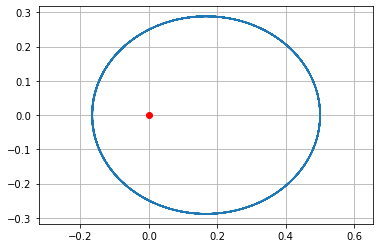
Vidíme, že řešení soustavy diferenciálních rovnic předpokládá, že řešení má podobu \(\vec U(t)\), které pro každé \(t\) nabývá hodnoty \({I\!\!R}^n\), kde \(n\) je počet řešených diferenciálních rovnic. Na druhé straně, z hlediska fyzikálního původu rovnic mlže být přirozené je mít v poli poskládané jinak.
Zatím jsme použili rozdělení \(\vec U\) na skalární proměnné:
x, y, vx, vy = U
Pokud bychom ale studovali pohyb hvězd v trojhvězdě (pro jednoduchost ve 2D), budeme v tomto přístupu mít například
x1, y1, x2, y2, x3, y3, vx1, vy1, vx2, vy2, vx3, vy3 = U
Počítat potom sílu mezi hvězdami může být nepřehledné. Je tu ale alternativa za použití konverze lineárně uspořádaného pole na matici nebo jinou vhodnou strukturu.
Nejprve si princip demonstrujeme s pomocí řetězců, poté jej použijme uvnitř funkce pohybova_rovnice_hvezd ke spočtení zrychlení
Díky operaci reshape budeme moci zapsat \(\vec x_i\) jako U[0,i] a \(\vec {\dot x}_i\) jako U[1,i]. Pot0, co práci v této pohodlnější reprezentaci fázového prostoru skončíme, v rámci příkazu return provedeme konverzi zpět na vektor.
[125]:
import numpy as np
vektorU = np.array( ['x1', 'y1', 'x2', 'y2', 'x3', 'y3', 'vx1', 'vy1', 'vx2', 'vy2', 'vx3', 'vy3'])
print('vektorU')
print( vektorU )
print( '\nvektorU.reshape((2,3,2))' )
print( vektorU.reshape((2,3,2)) )
vektorU
['x1' 'y1' 'x2' 'y2' 'x3' 'y3' 'vx1' 'vy1' 'vx2' 'vy2' 'vx3' 'vy3']
vektorU.reshape((2,3,2))
[[['x1' 'y1']
['x2' 'y2']
['x3' 'y3']]
[['vx1' 'vy1']
['vx2' 'vy2']
['vx3' 'vy3']]]
[114]:
from scipy.integrate import solve_ivp
import numpy as np
import math
pocet_hvezd = 3
pocet_souradnic = 2
# součin hmotností hvězd a grav. konstanty (v jednotkách AU, rok, hmotnost_Slunce)
GM_hvezd = np.array([1,1,1]) * 4*math.pi**2
def pohybova_rovnice_hvezd(t, U):
"""
Předpokládá U = [x1, y1, x2, y2, x3, y3, vx1, vy1, vx2, vy2, vx3, vy3] a pod.
Vrací časovou derovaci dle Newtona.
"""
U = U.reshape((2, pocet_hvezd, pocet_souradnic))
dUdt = np.zeros_like(U)
for i in range(pocet_hvezd):
for j in range(i):
rr = U[0,i] - U[0,j]
r2 = rr @ rr
r_3 = 1/(r2*math.sqrt(r2))
dUdt[1,i] += - GM_hvezd[j] * rr * r_3
dUdt[1,j] += + GM_hvezd[i] * rr * r_3
dUdt[0] = U[1]
return dUdt.reshape(2 * pocet_hvezd * pocet_souradnic)
dt = 1/365 # jeden den
tmax = 0.29 # dva roky
x_1, y_1 = 1, 0
vx_1, vy_1 = 0, -3.05216379919688
x_2, y_2 = -0.5, 0.3193874731184
vx_2, vy_2 = -7.16722802885, 1.52608189959845
x_3, y_3 = -0.5, -0.3193874731184
vx_3, vy_3 = 7.16722802885, 1.52608189959845
U0 = np.array([x_1, y_1, x_2, y_2, x_3, y_3, vx_1, vy_1, vx_2, vy_2, vx_3, vy_3])
sol = solve_ivp(pohybova_rovnice_hvezd, (0,tmax), U0, max_step=dt)
plt.plot(sol.y[0], sol.y[1], sol.y[0,-1:], sol.y[1,-1:],'o',color='blue')
plt.plot(sol.y[2], sol.y[3], sol.y[2,-1:], sol.y[3,-1:],'o',color='red')
plt.plot(sol.y[4], sol.y[5], sol.y[4,-1:], sol.y[5,-1:],'o',color='green')
plt.axis('equal')
plt.grid()
plt.show()
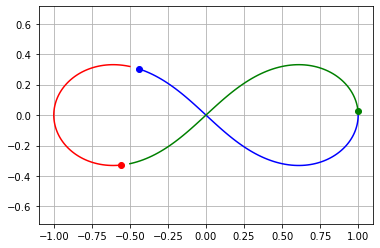
Cvičení: Zapište ekvivalentní kód pomocí řezů, tedy bez reshape. Například \(\vec x_i\) lze totiž zapsat jako U[2*i:2*i+2].
Protože požité počíteční polohy a rychlosti vedou na zajímavý pohyb, vytvoříme si ještě jeho animaci. Konverze obrázků do podoby videosouboru a jeho zobrazení jsou přenechány funkcím z knihoven matplotlib a IPython. Kód spoléhá na ten předchozí ohledně načtení knihoven, definice funkce pohybova_rovnice_hvezd, hodnoty dt a počátečních dat pro pohyb hvězd trojhvězdy U0. Navíc
Necháme diferenciální rovnici vyřešit na časovém úseku zhruba odpovídajícímu jedné periodě děje (pohyb trojhvězdy není obvykle periodický, zde jde o výjimku). Vhodně zvoleným parametrem
t_evalfunkcisolve_ivppožádáme, aby vrátila ekvidistantně navzorkované řešení. Co vzorek, to jeden snímek animace, viz příkazt_samples = np.linspace(0, tmax, frame_count).V cyklu
forpřipravíme seznam jednotlivých snímkůDo každého snímku vložíme výsledek čtyřech příkazů
plot. Ty namalují jednak celkovou trajektorii šedě a pak také barevně tři úseky odpovídající dráze hvězd během určitého časovému intervalu. Tak se na animaci dá znázornit rychlost pohybu. (Zvolený interval odpovídá indexůmi0:i1.)Data pro malování polohy hvězd a stop si za pomoci řezů před malováním připravíme (proměnné
pointatrace). Díky tou jsou argumenty příkazůplotsrozumitelnější.Seznam snímků pak nechá převést do videosouboru a zobrazit ve výsledkové části.
[128]:
# import dalších knihoven, nepoužitých v minulém příkladě
import matplotlib.animation as animation
from IPython.display import HTML
# parametry animace
fps = 50 # snimku za sekundu
duration = 5 # trvání 5 sekund
frame_count = int(duration*fps)
# pořídíme řešení na delším časovém intervalu
tmax = 0.90
t_samples = np.linspace(0, tmax, frame_count)
sol = solve_ivp(pohybova_rovnice_hvezd, (0,tmax), U0, max_step=dt, t_eval=t_samples)
# příprava na vytvoření animace
frames = [] # vytvořím prázdný seznam snímků
fig = plt.figure() # vytvořím prázdný obrázek
plt.grid()
plt.axis('equal')
# vytvoření animace snímek po snímku
for i in range(len(t_samples)):
i0 = max(0,i-fps//2)
i1 = i+1
trace = sol.y[:,i0:i1]
point = sol.y[:,i:i1]
this_frame = plt.plot(sol.y[0], sol.y[1], linewidth=0.4, color='gray')
this_frame += plt.plot(trace[0], trace[1], point[0], point[1],'o',color='blue')
this_frame += plt.plot(trace[2], trace[3], point[2], point[3],'o',color='red')
this_frame += plt.plot(trace[4], trace[5], point[4], point[5],'o',color='green')
frames.append(this_frame)
# snímky složíme do animace
ani = animation.ArtistAnimation(fig, frames, interval=1000//fps)
# ještě po sobě uklidíme, protože matplotlib nechal otevřený obrázek
plt.close()
# zobarzíme animaci v buňce Jupyteu
HTML(ani.to_html5_video())
[128]:
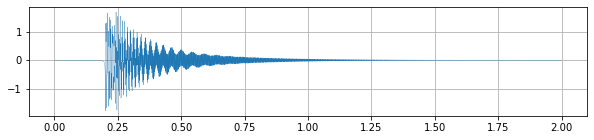
Jako zajímavost uveďme, že kromě animací můžeme v Jupyterových sešitech přehrávat i audiosignál. V následujícím příkladě je opět generován jako řešení diferenciální rovnice. Soustava tří oscilátorů je vybuzena úderem v podobě impulsu ve tvaru \(1/[(t-t_0)^2+\delta t^2]\), který má maximum v čase \(t_0\) a šířku řádově \(\delta t\).
[71]:
from scipy.integrate import solve_ivp
import numpy as np
import matplotlib.pyplot as plt
import math
import IPython
def dif_rovnice(t, U):
"""
Jednoduchá soustava 6 dif. rovnic pro 2 harmonické a jeden anharmonický
oscilátor s lineárními vazbami, tlumením a impulsním buzením.
"""
x, y, z, vx, vy, vz = U
ax = - (2*math.pi*440)**2 * (x-0.1*(y-z)) - 8*vx
ay = - (2*math.pi*440*4/3)**2 * (y-0.1*(x-z)) - 4*vy
az = - (2*math.pi*20)**2 * (z+z**3) - 24*vz
az += 1/((t-0.2)**2+1/4000**2) # impuls okolo t=0.2
return [vx, vy, vz, ax, ay, az]
f_sampling = 22050 # vzorkování 1/2 f_CD
dt = 1/f_sampling
tmax = 2 # dvě sekundy
t_samples = np.arange(0,tmax,dt) # ekvidistantní vzorkování pro audio
U0 = np.zeros(6)
sol = solve_ivp(dif_rovnice, (0,tmax), U0, max_step=dt, t_eval=t_samples)
plt.figure(figsize=(10,2))
plt.plot(sol.t, sol.y[0], linewidth=0.3)
plt.grid()
plt.show()
IPython.display.Audio(sol.y[1], rate=f_sampling)
[71]:
[ ]:
 Programování pro fyziky (1.r)
Programování pro fyziky (1.r) Obsah
Obsah