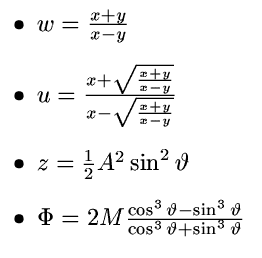
3. Doplňte do následujícího kódu správný výraz místo ?????
Lekce 3
Aritmetické operátory a typy
Cím se liší následující výrazy?
1*1
1/1
1>1
Především výraz (1>1) nemá hodnotu číselnou ale logickou.
Protože lomítko je symbolem pro reálné dělení, je výsledek podílu 1/1
"reálná jednička", zatímco u součinu je ta jednička celé číslo.
Operandy +-*/ mohou být čísla realná nebo celá, div a mod
mají jako operandy pouze čísla celá.
Za předpokladu, že proměnné x,y,i a j jsou deklarovány takto:
var i,j : integer;
x,y : real;
můžeme aritmetické oprace shrnout v následující tabulce
| význam | operand | výsledek | příklad--> typ výsledku | |
| + | sčítání | real, integer | real,integer | x+i --> real |
| - | odčítání | real,integer | real,integer | i-j --> integer |
| * | násobení | real,integer | real,integer | x*y --> real |
| / | reálné dělení | real,integer | real | i/j --> real |
| div | celočíselné dělení | integer | integer | i div j --> integer |
| mod | zbytek při dělení | integer | integer | i mod j --> integer |
Pro oparace +-* platí, že výsledek je celé číslo pouze pokud jsou oba operandy celá čísla.
Hodnota celočíselného podílu
i div j
je rovna hdonotě reálného podílu zaokrouhlené směrem k nule, tedy
i div j = trunc(i/j)
Pro záporná i a/nebo j je tato definice kompatibilní se vztahy
(-i)/j = - (i/j), i/(-j) = - (i/j)
Operace mod splňuje vztah
i mod j = i – (i div j) * j
Obvukle ji budme používat pouze pro j>0 a i>=0, kdy platí že
i mod j = 0..j-1
tedy jde o běžnou operaci zbytku po dělení a např.
17 mod 5 = 2 .
Pokud je j=0, způsobí operace
x / j
i div j
i mod j
krach programu.
Unární oprátory + - nemění typ.
Logické operátory
Typ boolean popisuje logický stav ano/ne, v řeči Pascalu true/false.
Jakkoli se interně reprezentují hodnota false jako 0 a hodnota
true jako 1 jsou v jazyce Pascal logické hodnoty svým typem izolovány od
celých čísel a běžné aritmetické oprece pro ně nejsou definovány. Proto
nelze psát
k := (i=imax) + (j=jmax);
( umožní nám to v budoucnu operace/funkce ord ).
Nad hodnotami false a true však pracují logické operátory:
1. Binární operátory: and, or, xor
| and | false | true |
| false | false | false |
| true | false | true |
| or | false | true |
| false | false | true |
| true | true | true |
| xor | false | true |
| false | false | true |
| true | true | false |
2. Unární operátor negace not:
| not | false | true |
| true | false |
Relační operátory (=, <>, <, <=, >, >=)
Porovnávají dvě hodnoty, přičemž podobně jako + či * umějí porovnat
reálné a celé číslo (přesněji dva jednoduché výrazy těchto typů).
Navíc také umějí porovnat logické hodnoty ve smyslu
false < true.
Ve všech případech je výsledkem porovnání logická (boolean) hodnota.
Celá čísla v počítači
V současné době je standardem používat k uložení celého čísla 32 bitů. Protože je to docela dlouhé dvojkové číslo, použijeme pro následující příklad pouze čtyři bity.
Ilustrace
Do čtyřech bitů lze uložit následujících 16 kombinací 0 a 1:
3210 hex unsigned signed
---- - -------- ------
0000 0 0 0
0001 1 1 1
0010 2 2 2
0011 3 3 3
0100 4 4 4
0101 5 5 5
0110 6 6 6
0111 7 7 7
1000 8 8 -8
1001 9 9 -7
1010 A 10 -6
1011 B 11 -5
1100 C 12 -4
1101 D 13 -3
1110 E 14 -2
1111 F 15 -1
Když potřebujeme do 4-bitového čísla uložit číslo s významem celého
čísla se znaménkem máme několik možností. V posledním slupci tabulky je
uveden dnes nejrozšířenější způsob - reprezentace celého čísla se
znaménkem pomocí tzv. dvojkového doplňku. Je to technologicky nejméně
nákladný způsob jak obvody počítače naučit pracovat zárověň s
čísly se znaménkem i bez znaménka. To proto, že stroj nemusí rozlišovat,
zda sčítá či odčítá číslo se znaménkem nebo bez:
Operace 1010+0010 = 1100 má podle okolností buď význam
10 + 2 = 12
a nebo
-6 + 2 = -4.
Protože pomocí 4 bitů můžeme reprezentovat čísla 0..15 resp -8..7 vedou některé operace k tzv. přetečení.
Pro čísla bez znaménka je to např. operace 15+15, jejíž
výsledek neleží v intervalu 0..15.
Pokud se natuto operaci díváme z pohledu operací se znaménkem, je vše
O.K., neboť (-2)+(-2)=-4.
Pro čísla se znaménkem je nedovolená např. operace 4+4=8, neboť jako horní mez rozsahu čtyřbitových oznaménovaných čísel je 7. Z hlediska čísel bez naménka je to ovšem operace dovolená.
Pro nás znamená typ integer 32 bitové číslo se znaménkem povolující
uložení celého čísla v rozsahu –2 147 483 648 ..
2 147 483 647.
V případě, že nějaká oprace, např. v příkazu k:=i*j vede k
přetečení, není obvykle spuštěn žádný poplach a program se posléze chová
podivně bez zjevných příčin, protože výsledek přiřazovacího příkazu je
jiný, než zamýšlený. Je ale možné donutit program, aby si tato možná
přetečení ohlídal, stráví se tím nějaký čas navíc, ale ušetří to čas
při hledání problémů. Až se budeme zabývat laděním programů bude
zapnutí kontroly na přetečení jedním z bodů v návodu.
Ve vyjímečných případech budeme potřebovat vědět, že jsou k dispozici i jiné celočíselné typy:
Identif.Typu Rozsah Formát uložení
-----------------------------------------------
Shortint –128..127 signed 8-bit
Smallint –32768..32767 signed 16-bit
Longint –2147483648..2147483647 signed 32-bit
Int64 –2^63..2^63–1 signed 64-bit
Byte 0..255 unsigned 8-bit
Word 0..65535 unsigned 16-bit
Longword 0..4294967295 unsigned 32-bit
Jak vidíme, typ Integer je v současné době totožný s typem Longint. Je pravděpodobné, že během několika let bude typ Integer odpovídat 64-bitovému číslu a neměli bychom spoléhat na to, že proměnné typu Integer jsou ukládány jako zrovna jako 32-bitové. Abychom však nemuseli hlídat každý součin 200*200 (nevejde se do SmallInt), budeme předpokládat, že těch bitů je nejméně 32, takže pozor na přetečení si budeme muset dávat až u součinů jako je 50000*50000.
S výjimkou typu Int64 obecně neplatí, že operace s kratším formátem
je rychlejší, takže důvody pro použití kratšího formátu čísla musí být v
algoritmu samém, ne jeho optimalizaci. Jednou z výjimek je úspora
paměti při uložení miliónů a miliónů celých čísel v poli (viz dále),
převážným důvodem ale bude respektování formátu vstupních dat: např.
komponenty RGB v bitmapě jsou typu Byte, zvuk v audiosouboru na
kompaktním disku je zase posloupnost dvojic (L,R) oznaménkovaných
16-bitových čísel ( typ SmallInt ).
Logické operace nad celými čísly
Z technických důvodů se čísla v počítači uskladňují ve dvojkovém
zápisu. Na jednotlivé bity lze pak aplikovat logické operátory and, or,
xor a not ve stejném smyslu jako pro true a false.
var x,y : Integer;
....
x := 21;
y := 12;
{ nyní platí }
x or y = 29
{ neboť
00000000 00000000 00000000 00010101 // 21 = 16+0+4+0+1
or 00000000 00000000 00000000 00001100 // 12 = 0+8+4+0+0
----------------------------------------------------------
00000000 00000000 00000000 00011101 // 29 = 16+8+4+0+1 }
x and y = 4
{ neboť
00000000 00000000 00000000 00010101 // 21 = 16+0+4+0+1
and 00000000 00000000 00000000 00001100 // 12 = 0+8+4+0+0
----------------------------------------------------------
00000000 00000000 00000000 00000100 // 4 = 0+0+4+0+0 }
x xor y = 25
{ neboť
00000000 00000000 00000000 00010101 // 21 = 16+0+4+0+1
xor 00000000 00000000 00000000 00001100 // 12 = 0+8+4+0+0
----------------------------------------------------------
00000000 00000000 00000000 00011001 // 25 = 16+8+0+0+1 }
not x = -22
{ neboť
not 00000000 00000000 00000000 00010101 // 21 = 16+0+4+0+1
---------------------------------------------------------------
11111111 11111111 11111111 11101010 //-22 = (-1)-16-0-4-0-1 }
Mimochodem, aby si programátoři šetřili klávesy 0 a 1, místo binárního
zápisu používají zápis šestnáctkový (hexadecimální). čtveřice bitů se
podle výše uvedené tabulky ozačí číslicí 0..9 nebo písmenem A-F. Proto
nám následující příkaz writeln vypíše TRUE:
writeln( not $15 = $FFFFFFEA );
Protože Wirth nepoužil znak $ ve své versi Pascalu, mohl být později
použit $ jako uvozovací znak při zápisu šestnáctkového čísla a výše
uvedený kód je správně.
Protože jde jen o zápis čísla pro kompilátor, a $15 je naprosto totéž
jako 21, zkuste uhodnout co udělá následující příkaz:
writeln( $15 );
Celá a reálná čísla
V jazyce Pascal se přes jeho přísnou kotrolu typů povoluje použít
celé číslo na místě reálného. Proto do reálné proměnné smíme
dosadit hodnotu s typem Integer, přesněji v přiřazovacím příkazu
idProm:=Vyraz
kde idProm je identifikátor reálné proměnné smí mít Vyraz
nejen reálný typ ale i typ celočíselný.
Zvláštním případem je podíl dvou celých čísel. V příkazu
E := 1/2*m*v*v;
se podíl 1/2 vyhodnotí na konstantu 0.5 a příkaz provede, co jsme zamýšleli. Protože však např. v jazycích FORTRAN a C se podíl 1/2 vyhodnotí jako 0 a do E se dosadí nula, je pro budoucího fyzika vhdoné zvyknout si psát např.
V := 4/3.0*Pi*r*r*r;
a nebo 4.0/3 atp.
Řešení problémů hrubou silou
Jako první při řešení nějakého problému uvažujeme algoritmus
spočívající v použití hrubé síly.
Jako ilustraci tohot přístupu uvažujme následující program, který hledá
všechny neuspořádané trojice kladných čísel, které leží na kouli o
poloměru 2003, pokud je chápeme jako kartézské souřadnice bodu v
prostoru a koule má střed v počátku.
Načtněme nejdříve obrysy takového postupu:
program Rozklady1;
var a,b,c,N :integer;
begin
N:=2003;
Writeln('Rozklady cisla ',N);
{pro vsechny trojice N>a>=b>=c>0 zkoumej zda plati}
for a:=1 to N-1 do
for b:=1 to a do
for c:=1 to b do
begin
if a*a+b*b+c*c=N*N then writeln(a,' ',b,' ',c);
end;
Writeln('konec');
end.
Následující variantu je stále možné považovat za použití hrubé síly, i když je cca 60x rychlejší.
program Rozklady2;
var a,b,c,N :integer;
begin
N:=2003;
Writeln('Rozklady cisla ',N);
{pro vhodne trojice N>a>=b>=c>0 zkoumej zda plati}
for a:=1 to N-1 do
begin
b:=1;
while (b<=a) and (N*N-a*a-b*b>0) do
begin
c:=trunc(0.5+sqrt(N*N-a*a-b*b));
if (c<=b) and (a*a+b*b+c*c=N*N) then writeln(a,' ',b,' ',c);
b:=b+1;
end;
end;
Writeln('konec');
end.
Navíc se následujícími příkazy můžeme přesvědčit, že oba programy dávají stejné výsledky. Zde použijeme trik s přesměrováním výstupu programu do souboru (To je to znaménko > mezi příkazem a názvem výstupního souboru). Necháme tak vytvořit dva soubory, jejichž názvy si samozřejmě můžeme zvolit libovolně, a posléze jejich obsah porovnáme. Práci s porovnáváním obsahu můžeme přenechat počítači, pokud si zjistíme, který program to za nás udělá. Seznam takovýchto užitečných programů dodám později, a pak se dozvíte, že v tomto případě je třeba použít program s názvem FC (pro příkazový řádek MS Windows).
C:\Projects\prog\pokusy>Rozklady1 > Vysledky1.txt |
Příkládky k přemýšlení
1. Jaké jsou typy následujících výrazů? Jsou všechny zapsány správně?
{deklarace}
var i,j,k : integer;
x,y,z : real;
be : boolean;
{ nyní následují výrazy }
i+j
i*j
i/j
i+y
i*y
i/y
i mod y
be and i>j
i>j and x>y
be or not 2*be
2. Zapište jako přiřazovací příkazy následující vzorečky (volbu
identifikátorů a počet přiřazení je na vás)
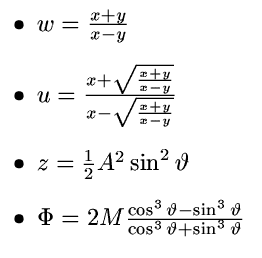
3. Doplňte do následujícího kódu správný výraz místo ?????
const N = 54354;
var i,j,k,pocetprocent: Integer;
begin
{...}
for i:=1 to N do
begin
{zkoumej moznost i}
{...}
{uz jsem to prozkoumal, ted to jeste oznamim obsluze, ktera ceka na vysledek}
pocetprocent := ????? ;
Write('Prave jsem prozkoumal ',pocetprocent,'% moznych hodnot. ',#13);
end;
{...}
end.
Po správném doplnění otazníků můžete program použít jak je. Psaní
hlášení o postupu výpočtu zabere programu tolik času, že vlastně ani
není potřeba aby něco užitečného dělal a i tak poběží pár sekund.
Vyzkoušejte !
Vyzkoumejte, co to je ten #13 !!! Třeba tak, že jej nejprve odstraníte,
poté nahradíte třeba #33 a uvidíte ten rozdíl.
4. Všichni znáte součtové vzorce, zvažte následující kód:
const k=100;
alpha=0;
beta=0.1;
var sa,ca,sb,cb,soucet : real;
n:integer;
begin
{do promennych sa a ca strcim sin prip cos alpha:}
sa := sin(alpha);
ca := cos(alpha);
{do promennych sb a cb strcim sin prip cos beta:}
sb := sin(beta);
cb := cos(beta);
{ nyni mohu spocitat
soucet := sin(alpha+beta)+sin(alpha+2*beta)+...+sin(alpha+N*beta) ,
kdyz vyuziji souctovych vzorcu takto:}
soucet:=sa;
for n:=1 to k do begin
sa := sa*cb+ca*sb;
ca := ca*cb-sa*sb;
soucet := soucet + sa;
end;
{...}
writeln(soucet);
end.
Co je na tomhle kódu špatně? Přesněji, kde je v cyklu chyba, která
způsobí, že nedostanu součet sinů? Opravte tu chybu.