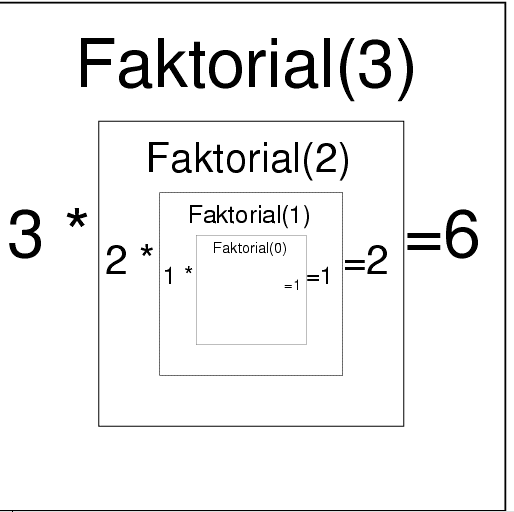
Rekurentní vztahy
Nejjednodušším příkladem je samozřejmě funkce faktoriál:.
n! = n (n-1)!
0! = 1
Jiným standardním příkladem je Fibonacciho posloupnost:
F(n) = F(n-2)+F(n-1)
F(0) = 0
F(1) = 1
Jakkoli je nasnadě použít pro výpočet prostředky rekurse jazyka Pascal, nebudeme je v toěchto případech používat. Programová rekurse je znázorněna pro faktorial takto:

a odpovídá následujícímu kódu:
function faktorial(a:integer):real;
begin if a<=1 then faktorial := 1
else faktorial := a*faktorial(a-1);
end;
Pro Fibonacciho posloupnost takto

kde je nevhodnost programové rekurse naprosto zřejmá.
Cvicení: Vyzkoušejte si napsat rekurentní
versi funkce Fibonacci(n : integer).
Cvicení: Kolikrát se zavolá funkce Fibonacci,
kdyz se takto pokoušíme spočíst Fibonacci(6)?
Jak tedy převedeme matematický rekurentní vztah na návod pro počítač? Nejjednodušší je samozrejme případ funkce faktorial
function faktorial(a:integer):real;
var i : integer;
s : real
begin
s:=1;
for i:=2 to a do s := s*i;
faktorial := s;
end;
Takto zapsaný postup má jediný háček: vrací rozumnou
hodntu i pro záporné hodnoty parametru a. Podobně
jako by nebylo nejlepší, kdyby nám sqrt vracelo nulu
pro záporné parametry (dáváme přednost krachu programu),
měli bychom přidat test na záporné hodnoty a a
program případně ukončit.
Cvičení: Zkuste na cyklus prevést výpocet
funkce Fibonacci.
Zde si ukázeme, jak převést na cyklus složitější variantu Fibonacciho vztahu. Zadání, které nalezneme v učebnici fyziky zní:
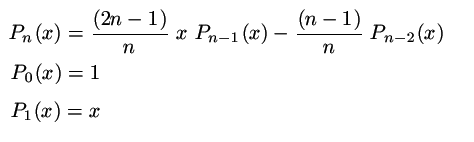
kde Pn(x) je tzv. Legendreuv polynom a během studia jej mnohokrát potkáte. Pro nás je úloha omezena na nalezení hodnoty Pn(x) pro dané celé n>=0 a reálné x. Jak je vidět, je potřeba rozlišit případy n=0, n=1 a zbytek, kdy použijeme uvedenou formulku opakovaně (n-1)-krát. Zde je jedna z variant:
function LegendreP( m : integer; x : real ) : real;
var Pn2, Pn1,Pn : real;
n : integer;
begin Pn := 1; {P0(x)}
if m = 1 then Pn := x; {P1(x)}
Pn2 := 1;
Pn1 := x;
for n := 2 to m do begin Pn := ((n+n-1)*x*Pn1 - (n-1)*Pn2 )/n; Pn2:= Pn1; {Pn->Pn1->Pn2} Pn1:= Pn; end;
LegendreP := Pn;
end;
Příkaz cyklu for se nám postará o zvyšování n od 2 až do m, ale s každým zvýšením hodnoty n je potřeba také posunout hodnoty v proměnných, které si "pamatují" hodnoty Pn-2 a Pn-1.
Pro vykreslení použijeme následující program
program MalujLegendreovyPolynomy;
const xa = -1;
xb = 1;
N = 400;
function LegendreP( m : integer; x : real ) : real;
...... viz výše ....
var k,i : integer;
x,y : real;
begin
for k := 0 to 12 do begin
for i := 0 to N do begin
x := xa + (xb-xa)*i/N;
writeln(x,' ',LegendreP(k,x));
end; {graf pro pevne x}
writeln; {vypiš dva prázdné rádky}
writeln;
end; {dalsi k}
end.
Ten vypíše tabulku hodnot Funkce P0(x), poté dva prázdné řádky, pak tabulku hodnot funkce P1(x), pak dva prázdné řádky atd. až nakonec tabulku funkčních hodnot P12(x). Zadáme-li programu guplot příkaz plot "legendre.dat", kde soubor legndre.dat obsahuje výstup našeho programu, dostaneme následující obrázek
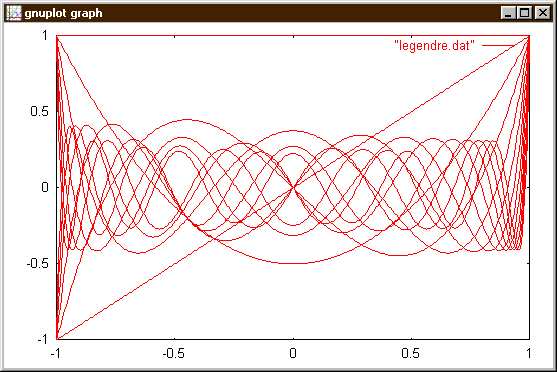
Protože jsme ale oddělili jednotlivé tabulky hodnot dvěma prázdnými řádky, můžeme si z toho zmatku vybrat jen ty křivky, které nás zajímají a to pomocí slova index následujícího za názvem datového souboru. Např.
plot "legendre.dat" index 1,"legendre.dat" index 2,"legendre.dat" index 3, "legendre.dat" index 12
nám vymaluje tabulky hodnot polynomu P1, P2, P3 a P12. Ještě se k tomu vrátíme v povídání o polích, ale je dobré vědet, že první sekci dat odpovídá index 0 a tak shodou okolností se index sekce shoduje s řádem Legendreova polynomu.
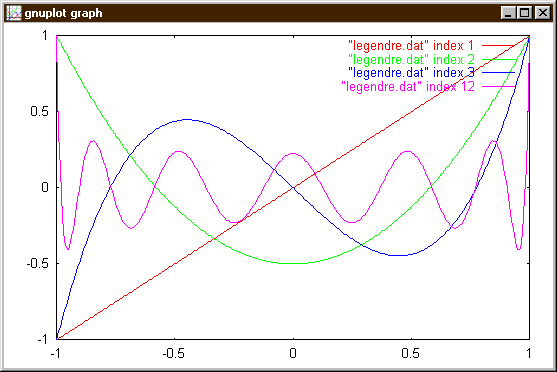
Pozor: někdy se může stát, že rekurentní vztah podobný výše uvedenému pro Legendrovy polynomy nefunguje, neboť s rostoucím n může do závratných výšek narůst úplně drobná počátecní nepřesnost. Diskuse tohoto jevu je ovšem mimo možnosti této prednášky.