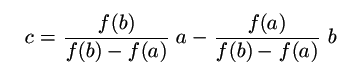
Tvoří velmi důležitou třídu algoritmů. Povětšinou spočívají v aplikaci zázračné formulky, která říká jak z méně přesného výsledku vyrobit výsledek přesnější a jejím opakování až do dosažení požadované přesnosti. Zde si ukážeme jak několik takových formulek a algoritmů na nich založených.

Půlení intervalu

Nabývá-li spojitá funkce v bodě a zápornou a v bodě b kladnou hodnotu, musí se nejméně jeden kořen funkce nacházet někde mezi těmito dvěma hodnotami. Zkusíme-li uprostřed spočíst funkční hodnotu uprostřed intervalu v bodě c=(a+b)/2 buď rovnou nalezneme kořen, nebo nalezneme kratší podinterval, ve kterém se kořen zaručeně nachází. Podle znaménka c je to buď <a,c> nebo <c,b>. Pokud je tento podinterval ještě stále moc velký, celý postup opakujeme. Délky intervalů tvoří geometrickou posloupnost s kvocientem 1/2. Proto každých deset iterací přidá tři desetinná místa a po 52 iteracích dosáhneme přesnosti s níž je uložena neznámá, pokud uvažujeme, že jsme začali s intervalem <1,2>. Pokud bychom se na reálnou proměnnou dívali ve dvojkovém zápise, dá se zhruba říci, že v každém kroku iterace přidáme jeden bit přesnosti. Toto je nejpomalejší metoda hledání kořene ale musíme ji ovládat. Pokud totiž máme dost času a nebo je funkce do té míry ošklivá, že rychlejší metody nemůžeme použít, je rozumné použít půlení ntervalu pro jeho spolehlivost.

Newtonova metoda

Na rozdíl od půlení intervalu, vyžaduje newtonova metoda, aby poblíž kořene byla funkce dostatečne hladká. To proto, že metoda předpokládá, že funkci lze nahradit prvním diferenciálem a ten jako lineární rovnici použít k hledání kořene:

f(x1) = f(xo+dx) = f(xo) + f'(xo) dx = 0

a tedy

x1 = xo+dx = xo - f(xo)/f'(xo)

Jako příklad použijeme snad nejjednodušší možný problém - výpočet převrácené hodnoty čísla. Představme si na chvíli, že Pascal spolu s umocňováním neovládá ani dělení. Co teď? Podíl a/b můžeme vyjádřit jako součin a s převrácenou hodnotou b. Jak ale spočíst převrácenou hodnotu? Zkusíme hledat kořen rovnice
f(x) = b-1/x
Newtonova motetoda říká,. že pokud vezmeme xo dostatečne blízko kořene bude číslo

x1 = xo+dx = xo - f(xo)/f'(xo) = x + x(1-bx)

ještě mnohem blíže. Vidíme, že na vypočtení nám stačí pouze násobení a sčítání. Že by bylo možné převést dělení na sérii násobení a sčítání?

Nejdříve to zkusíme pro konkrétní hodnotu např. 0.9 a první přiblížení převrácené hodnoty odhadneme na 1.1. K jaké posloupnosti přiblížení převrácené hodnoty 1/0.9 povede Newtonova metoda?

xo =1
x1 =1.1
x2 =1.111
x3 =1.1111111
x4 =1.111111111111111

Vidíme, že zatímco půlení intervalu by přidalo 0.3 cifry na iteraci, dosáhli jsme v každém kroku zdvojnásobení počtu platných cifer a potřech iteracích musíme skončit, protože již neumíme čísla ukládat přesněji. Chování chyby se dá studovat obeně, my ale pro jednoduchost použijeme konkrétní funkci odpovídající výpočtu převrácené hodnoty.

Metoda regula falsi

Ne vždy ale dokážeme spočítat hodnotu derivace. Jistým vylepšením metody půlení intervalu je předpokládat, že funkce mezi body a a b vypadá téměř jako úsečka a zkoušet místo půlky intervalu vzít jako kandidáta na kořen prusečík této sečny s osou x, tedy

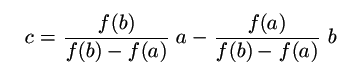
Nyní se podobně jako u půlení intervalu rozhodneme podle znaménka f(c) tak aby kořen ležel ve zvoleném intervalu. Pro funkce, které nemění v blízkosti kořene znaménko druhé derivace tato metoda neustále upravuje jen jednu mez, jak uvidíme v našem příkladu s dělením:

[a0,b0] = [1, 1.200000000000000]
[a1,b1] = [1, 1.120000000000000]
[a2,b2] = [1, 1.112000000000000]
[a3,b3] = [1, 1.111200000000000]
[a4,b4] = [1, 1.111120000000000]
[a5,b5] = [1, 1.111112000000000]
[a6,b6] = [1, 1.111111200000000]
[a7,b7] = [1, 1.111111120000000]
[a8,b8] = [1, 1.111111112000000]
[a9,b9] = [1, 1.111111111200000]
[a10,b10] = [1, 1.111111111120000]
[a11,b11] = [1, 1.111111111112000]
[a12,b12] = [1, 1.111111111111200]
[a13,b13] = [1, 1.111111111111120]
[a14,b14] = [1, 1.111111111111112]
[a15,b15] = [1, 1.111111111111111]

Zjednodušeně se dá říci, že v v blízkosti kořene se chyba snižuje geometrickou řadou, přičemž kvocient je dán mírou nelinerity. Jakkoli nemůže tato metoda kořen "ztratit", může se tedy stát, že se metoda regual falsi chová i hůře než půlení intervalu.

Metoda sečen

To že jeden z krajních bodů zůstával v minulé metodě trčet na místě, výrazně snižovalo rychlost konvergence. Pokud upstíme od požadavku různých znamének funkce f v bodech a a b, můžeme mít vždy po ruce poslední a předposlední aproximaci kořene a z nih počítat odhad polohy kořene podle stejného vzorce. Ten navíc upravíme na následující tvar:

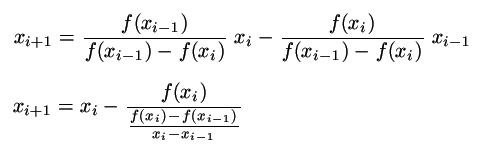
Všimněte si, že jmenovatel ve složeném zlomku je aproximací derivace funkce. Protože se nyní obě hodnoty přibližují kořeni, nepřekvapí, že účinnost metody se blíží Newtově metodě.

[a0,b0] = [1.000000000000000, 1.200000000000000]
[a1,b1] = [1.200000000000000, 1.120000000000000]
[a2,b2] = [1.120000000000000, 1.110400000000000]
[a3,b3] = [1.110400000000000, 1.111116800000000]
[a4,b4] = [1.111116800000000, 1.111111114751999]
[a5,b5] = [1.111111114751999, 1.111111111111092]
[a6,b6] = [1.111111111111092, 1.111111111111111]

Cvičení: Napište programy, které vypíší postup hledání kořene, a zkotrolují, zda jsem si ta výše uvedená data nevycucal z prstu.