Poznamky k prednasce

" content="text/html; charset=windows-1250"> Poznamky k prednasce - draft Algoritmus, program

Jak používat Delphi

Především: zde je možno program stáhnout a získat registrační klíč

Instalace
je mimo rámec téhle přednášky, pokud ale máte štěstí, stačí odpovídat střídavě
Yes/Accept/Next a ve vhodném okamžiku zadat klíč, který dojde emailem.
Za pozornost stojí, že spuštením staženého souboru
BorlandDelphiPe...Edition.Exe
pouze rozbalíte archiv, a někde vytvoříte adresář "Borland Delphi Personal Installer",
ve kterém je třeba spustit program "INSTALL.EXE".

Začínáme!
(Pár poznámek k prvnímu oťukávání)

Adresář, soubor ( cesta, textový a spustitelný soubor )

Command prompt (shell )
Příkazy na komandlajně

dir [ls -l]
mkdir
copy [cp]
move [mv]
del [rm]
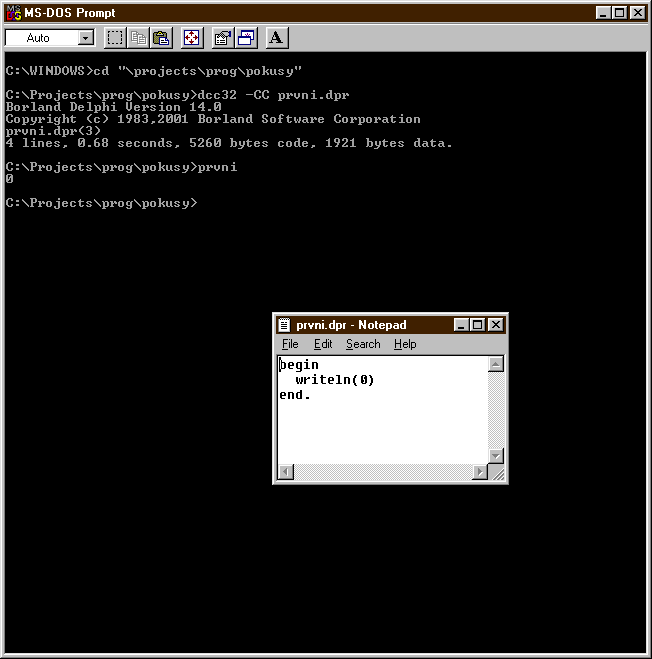
dcc32 -CC prvni.dpr [gpc prvni.pas]
notepad [nedit]

Textový editor

Poznámka pro lenochy: chcete-li přeskočit předchozí experimenty s shellem, nezapoměňte si vytvořit ve vhodném adresáři soubor prvni.dpr (ta příppona je kritická)

Návod pro klikoše

Windows umožňují asociovat s příponou souboru nějaký program. Dvojité (obvykle) kliknutí na nějaký soubor pak tento asociovaný program spustí a tento program pak vhodně použijevámi odkliknutý soubor. Podobně se chovaní i Delphi(R). Máme-li tedy již vytvořený soubor "prvni.dpr", stačí na něj kliknout a začnou se dít věci.

Bohužel, nyní musíme vývojovému prostředí Delphi vysvětlit, že jsme začátečníci a budeme psát jednouché programy s textovým a nikoli grafickým vstupem a výstupem.
Nejdříve klikneme pravým (tím neobvyklým) tlačítkem myši vedle 1 cm napravo vedle nápisu Help

a zrušíme fajfku u položky "Component Pallete".
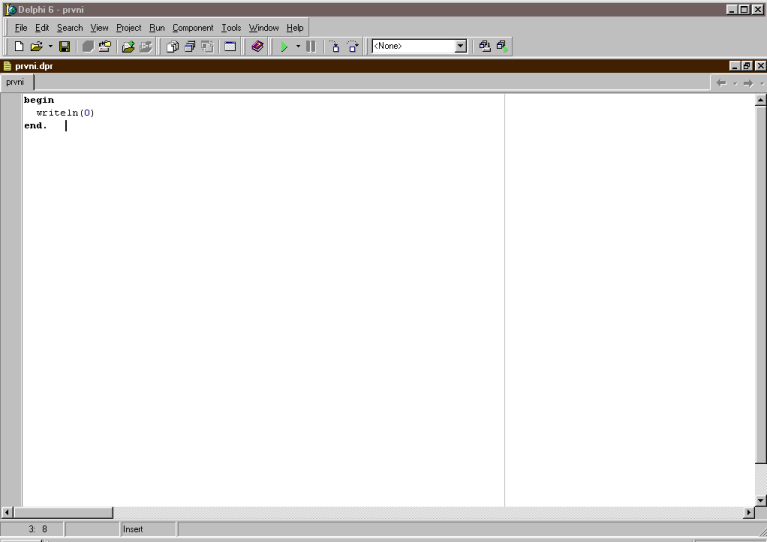
Poté kliknutím na křížek zavřeme obě malá okna nalevo a podle vašeho vkusu i zvětšíme okno s naším programem "prvni.dpr". Estéti ještě mohou myší přenést panýlky nástrojů z třetí řady počítáno svrchu za jejich levý okraj o řádek či dva výše. Poté naše pracovní plocha vypadá takhle:

Nyní klikneme na čudlík vedle nápisu "None" a na dotaz odpovíme třeba takto:

Nyní můžeme celé vývojové prostředí Delphi zavřít a vyzkoušet si, že při příští aktivaci souboru prvni.dpr (a vlastně i druhy.dpr, pokud si takový mezitím nějak vytvoříme) se vše obnoví v tomto začátečnickém rozložení pracovní plochy.

Nyní je již jen potřeba v menu pod položkou Project/Options nebo (současným) stisknutím klávesové zkratky Control-Shif-F11 aktivovat menu nastavemní a v něm zvolit záložku LINKER.

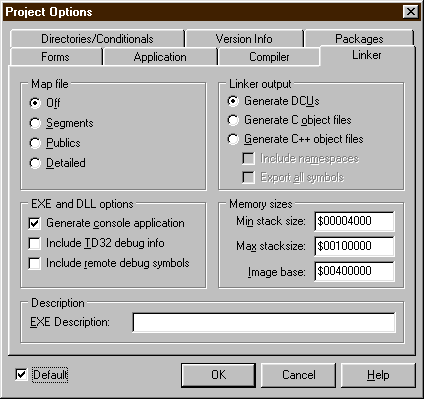
Zde musíme zaškrtnout dvě fajfky:

Genete console applications

Default

A pak nastavení potvrdit tlačítkem OK.

Tímto jsme jedné z částí překladače oznámili, že budeme psát programy určené k běhu v okně příkazového řádku, "konsoli".

Tím jsme hotovi.

Nezapoměňte, že běh programu je obvyle velmi rychlý a pokud si chceme výsledky prohlédnout, musíme na poslední řádek programu napsat kouzelné slůvko:

readln;

Začneme kolejištěm pro pascalovksý program:

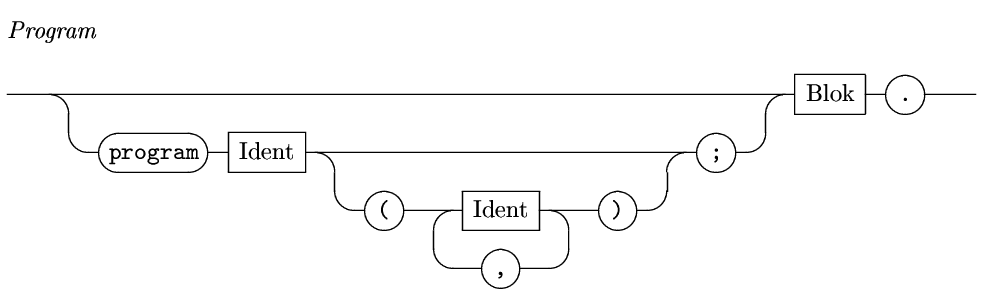
Protože je uvozovací část nepovinná, je správně jak následující program

program SHlavickou;
begin
  writeln('Jsem spravny program!');
end.

tak i tento kratký

begin writeln('Jsem usporny program!') end.

Předchozí programy byly těmi nejjednoduššími, jaké si lze představit. Neobsahují žádnou deklaraci a ten druhý se skládá pouze ze složeného příkazu. Tento složený příkaz ale bývá předcházen deklaračním oddílem, který jak později uvidíme, tvoří těžiště struktrurovaného programu.

V naší zatím velmi zjednodušené verzi Pascalu budeme uvažovat pouze proměnnéakonstanty a tak deklarační oddíl popisuje následující "kolejiště":

Konstanty jsou zkratky za konstantní výrazy. Existují dobré důvody proč používat konstanty:
Srozumitelnost, modifikovatelnost, pohodlí a bezpečí.

const HorniMez      = 12;
      EulerovaKonst = 0.577215664901532861;

Proměnné představují místa pro uložení hodnoty, jak později uvidíme, ne nezbytně numerické povahy.

Identifikátory proměnných by měly stručně napovídat, co jsou proměnné zač. Při řešení jednoduchých úloh vystačíme ale s konvencí z hodin matematiky. Indentifikátory typu jsou prozatím shůry dány tyto:

Integer ... proměnná tohoto tupu umí ulořit celá čísla v rozsahu –2 147 483 648..2 147 483 647

Real ... reálné proměnné mají co nejlépe uložit reálné číslo. Poskytují přesnost zhruba 15 desetinných míst a pokrývají rozsah řádů zhruba 1E-300 .. 1E300

Boolean ... V Pascalu je logická hodnota representována zvláštním typem který nabývá dvou hodnot

program SKonstantouADvemaPromennymi;
const N = 10;
var   i,s : integer;
begin
  i:=1;
  s:=0;
  while i<=N do 
  begin
    s:=s+i;
    i:=i+1;
  end;
  writeln('Soucet cisel od 1 do ',N,' je ',s);
end.

Tento velmi jednoduchý program nám kromě důvodů pro použití konstant ilustruje i použití složeného příkazu, který tvoří nejen závěrečnou (výkonnou) část pascalovského bloku, ale také umožňuje v cyklu while vykonávat více jak jeden příkaz:

Jak jsme viděli, program se skládá z hlavičky, deklarací a složeného příkazu, což je sekvence příkazů oddělená středníky a uzavřená mezi slova begin a end a tečky za programem.

A co je to ten Příkaz ?

Za prvé, jak vidíme, nic (prázdný příkaz) je také příkaz.

Jednoduché příkazy jsou v podstatě dva, strukturovaných příkazů je více, mezi ty základní patří samotný složený příkaz, podmíněný příkaz a příkazy cyklu.

Jednoduché příkazy

Ještě nejméně týden pro nás bude designátor totožný s identifikátorem, až se dozvíme, že jsou i další prvky jazyka, hodí se vědět, kde jazyk vyžaduje identifikátor, a kde můžeme použít "něco obecnějšího".
Obě uvedené formy jednoduchého příkazu ilustrují následjující dva řádky:

c := (a+b)/2;
Writeln( 'Prumer cisel ',a,' a ',b,' je ',c);

Strukturované příkazy - Podmíněný příkaz

má dvě varinaty. Krátkou (if ... then ... )

if a<b then a:=b;

a dlouhou (if ... then ... else ...)

if b*b-4*a*c>=0 then writeln('Rovnice ma reseni')
                else writeln('Rovnice nema reseni');

Problém je, že není úplně zřejmé, zda je správně tato

if a>0 then
         if b>0 then c:=1
       else c:=2;

nebo naopak tato indentace

if a>0 then
         if b>0 then c:=1
                else c:=2;

Podle pravidla, že v syntaktických diagramech opuštíme dosaženou úroveň až když musíme, je správně druhá verse. Abychom dosáhli účinku zamýšleného indentací prvního příkladu, musíme psát

if a>0 then
         begin
           if b>0 then c:=1
         end
       else c:=2;

Případně můžeme použít prázdný příkaz

if a>0 then
         if b>0 then c:=1
                else
       else c:=2;

Strukturované příkazy - Cykly

jsou důležitým prvkem jazyka. Představují opakování nějakého příkazu, které je ve správnou chvíli ukončeno. Strukturované příkazy rozlišují vlastní příkaz(y), které se mají opakovat a kontrolní část, která určuje za jakých podmínek se má příkaz provádět. Později uvidíme, že toto striktní oddělení, zvyšující "teoretické" kvality jazyka, bude povoleno porušit i jinak než pomocí goto.

Cyklus While

nejdříve se vyhodnotí podmínka a je-li splněna (hodnota true), provedede se příkaz, pak se znovu vyhodnotí podmínka atd. Nesplnění podmínky znamená konec provádění tohoto strukturovaného příkazu. V příkazu následujícím za přikazem while tak mohu předpokládat, že Vyraz má hodnotu nepravda (false).

Cyklus Repeat

nejdříve se vykonají všechny příkazy mezi klíčovými slovy repeat a until a pokud následně podmínka není splněna (Vyraz má hodnotu false), opakuje se provádění příkazů v cyklu atd. V příkazu následujícím za příkazem repeat tak mohu předpokládat, že Vyraz má hodnotu pravda (true).

repeat
 writeln(i); 
 i:=i+1;
until i>10;

je tedy rovnocenný příkazům

writeln(i);
i:=i+1;
while i<=10 do begin
    writeln(i);
    i:=i+1;
end;

Cyklus For
Je určen jako zkratka cyklu while v případě, kdy potřebujeme projít všecha celá čísla v nějakém intervalu

a umožní nám zjednodušit náš sčítací program

program SKonstantouDvemaPromennymiACyklemFor;
const N = 10;
var   i,s : integer;
begin
  s:=0; {na tohle nesmím zapomenout}
  for i:=1 to N do s:=s+i;
  writeln('Soucet cisel od 1 do ',N,' je ',s);
end.

Příkaz for je zkratkou cyklu while a tak při nevhodné konstalaci mezí nemusí být příkaz ani jednou vykonán.

Příklad: následující program nám odhalí, kteráže trojciferná čísla jsou stejně jako třeba číslo 153 součtem třetích mocnin svých cifer.

program cisla;

var a,i,j,k:integer;

begin
  for i:=1 to 9 do {např. 024 není trojciferné, tak začínám od 1}
    for j:=0 to 9 do
      for k:=0 to 9 do
        begin
          a:=i*100+j*10+k;
          if a=i*i*i+j*j*j+k*k*k then writeln(a);
        end;
end.

Pozn.: Algoritmus, který tento program popisuje, patří do třídy těch nejpotupnějších, neboť jej lze zapsat slovy: zkus všechny možnosti. (Slang: Brute force) Bohužel v diskrétních úlohách někdy ani lepší nenajdeme. Naštěstí není celých čísel "tak moc" jako těch reálných.

Výrazy

V předcházejících příkladech programů jsme používali m.j. přiřazovací příkaz a ten má na pravé straně výraz. Jde o přirozené zobecnění matematické notace do formy textu "vytisknutelného na dálnopise", zůstávají pojmy operand, operace, priorita.

Především, operace "porovnání" (>, <, <=, ...) jsou v Pascalu operátory s nějnižší prioritou. V syntaktickém diagramu to vypadá takhle:

Teď přichází na řadu obvyklé sčítání, odčítání a analogické logické operace

Termy, tedy sčítance mohou být součinem, podílem atp. jednotlivých faktorů.

Zde je třeba upozornit na operaci zbytku celočíselného dělení mod:

program CislaII;

var a,i,j,k:integer;

begin
  for a:=100 to 999 do begin
     i := a div 100; {stovky}
     j := (a div 10) mod 10; {desitky}
    {j := (a mod 100) div 10; }
     k := a mod 10; {jednotky}
     if a=i*i*i+j*j*j+k*k*k then writeln(a);
  end;
end.

program EuklidII;

var a,b :integer;

begin
  a := 11088;
  b := 17017;
  while a<>b do 
    if a>b then a:=(a-1) mod b + 1
           else b:=(b-1) mod a + 1;
  writeln(a);
end.

program EuklidIII;

var a,b,c :integer;

begin
  a := 11088;
  b := 17017;
  repeat
    c := a mod b;
    a := b;
    b := c;  {vyznam: (a,b) := (b,a mod b) }
  until b=0;
  writeln(a);
end.

No a konečně každý faktor může být identifikátor proměnné či konstanty, číslo atp.

Nejříve si připomeňme, že designátor je prozatím totéž, co identifikátor. První řádek (horní kolej) pak říká, že pravé strany následujících přiřazovacích příkazů jsou správné faktory, tedy i termy, tedy i jednoduché výrazy a konečně tedy i správné výrazy:

s:=a; 
y:=sin(x);
b:=InRange(y,-1,1);

Jak víme ne každý syntakticky správný kus kódu nám překladač schválí, třeba

var a:integer;
begin
  a:=a(1);
end.

není správný program. Identifikátor před závorkou totiž musí být identifikátor funkce. To že deklarujeme proměnnou či konstantu vlastně znamená, že uvedenému identifikátoru přiřadíme význam. Některé identifikátory jsou však definovány "samy od sebe". Mezi ně patrí i tzv. standardní funkce. Zde jen seznam některých z nich:

Následující funkce vrací reálnou hodnotu
ArcTan     arkustangens
Cos          cosinus
Sin         sinus
Exp        exponenciála
Ln          přirozený logaritmus
Sqrt       druhá odmocnina
Int            celá část čísla
Round      nejbližší celé číslo

Protože druhá mocnina celého čísla je vždy celé číslo,
je typ výsledku volání funkce sqr dán typem parametru.
Sqr druhá mocina

Aritmetické operátory a typy

Cím se liší následující výrazy?

    1*1
    1/1
    1>1

Především výraz (1>1) nemá hodnotu číselnou ale logickou.
Protože lomítko je symbolem pro reálné dělení, je výsledek podílu 1/1
"reálná jednička", zatímco u součinu je ta jednička celé číslo.

Operandy +-*/ mohou být čísla realná nebo celá, div a mod mají jako operandy pouze čísla celá.
Za předpokladu, že proměnné x,y,i a j jsou deklarovány takto:

  var i,j : integer; 
      x,y : real;

můžeme aritmetické oprace shrnout v následující tabulce

	význam	operand	výsledek	příklad--> typ výsledku
+	sčítání	real, integer	real,integer	x+i --> real
-	odčítání	real,integer	real,integer	i-j --> integer
*	násobení	real,integer	real,integer	x*y --> real
/	reálné dělení	real,integer	real	i/j --> real
div	celočíselné dělení	integer	integer	i div j --> integer
mod	zbytek při dělení	integer	integer	i mod j --> integer

Pro oparace +-* platí, že výsledek je celé číslo pouze pokud jsou oba operandy celá čísla.

Hodnota celočíselného podílu

   i div j

je rovna hdonotě reálného podílu zaokrouhlené směrem k nule, tedy

   i div j  = trunc(i/j)

Pro záporná i a/nebo j je tato definice kompatibilní se vztahy
(-i)/j = - (i/j), i/(-j) = - (i/j)

Operace mod splňuje vztah
i mod j = i – (i div j) * j

Obvukle ji budme používat pouze pro j>0 a i>=0, kdy platí že
i mod j = 0..j-1
tedy jde o běžnou operaci zbytku po dělení a např.
17 mod 5 = 2 .

Pokud je j=0, způsobí operace
x / j
i div j
i mod j
krach programu.

Unární oprátory + - nemění typ.

Logické operátory

Typ boolean popisuje logický stav ano/ne, v řeči Pascalu true/false.
Jakkoli se interně reprezentují hodnota false jako 0 a hodnota true jako 1 jsou v jazyce Pascal logické hodnoty svým typem izolovány od celých čísel a běžné aritmetické oprece pro ně nejsou definovány. Proto nelze psát

  k :=  (i=imax) + (j=jmax);

( umožní nám to v budoucnu operace/funkce ord ).

Nad hodnotami false a true však pracují logické operátory:

1. Binární operátory: and, or, xor

and	false	true
false	false	false
true	false	true

or	false	true
false	false	true
true	true	true

xor	false	true
false	false	true
true	true	false

2. Unární operátor negace not:

not	false	true
	true	false

Relační operátory (=, <>, <, <=, >, >=)

Porovnávají dvě hodnoty, přičemž podobně jako + či * umějí porovnat reálné a celé číslo (přesněji dva jednoduché výrazy těchto typů).
Navíc také umějí porovnat logické hodnoty ve smyslu
false < true.

Ve všech případech je výsledkem porovnání logická (boolean) hodnota.

Celá čísla v počítači

V současné době je standardem používat k uložení celého čísla 32 bitů. Protože je to docela dlouhé dvojkové číslo, použijeme pro následující příklad pouze čtyři bity.

Ilustrace

Do čtyřech bitů lze uložit následujících 16 kombinací 0 a 1:

3210   hex    unsigned     signed
----    -     --------     ------ 
0000    0        0            0  
0001    1        1            1
0010    2        2            2    
0011    3        3            3
0100    4        4            4    
0101    5        5            5
0110    6        6            6    
0111    7        7            7
1000    8        8           -8     
1001    9        9           -7 
1010    A       10           -6  
1011    B       11           -5  
1100    C       12           -4  
1101    D       13           -3      
1110    E       14           -2  
1111    F       15           -1

Když potřebujeme do 4-bitového čísla uložit číslo s významem celého čísla se znaménkem máme několik možností. V posledním slupci tabulky je uveden dnes nejrozšířenější způsob - reprezentace celého čísla se znaménkem pomocí tzv. dvojkového doplňku. Je to technologicky nejméně nákladný způsob jak obvody počítače naučit pracovat zárověň s čísly se znaménkem i bez znaménka. To proto, že stroj nemusí rozlišovat, zda sčítá či odčítá číslo se znaménkem nebo bez:
Operace 1010+0010 = 1100 má podle okolností buď význam
10 + 2 = 12 a nebo
-6 + 2 = -4.

Protože pomocí 4 bitů můžeme reprezentovat čísla 0..15 resp -8..7 vedou některé operace k tzv. přetečení.

Pro čísla bez znaménka je to např. operace 15+15, jejíž výsledek neleží v intervalu 0..15.
Pokud se natuto operaci díváme z pohledu operací se znaménkem, je vše O.K., neboť (-2)+(-2)=-4.

Pro čísla se znaménkem je nedovolená např. operace 4+4=8, neboť jako horní mez rozsahu čtyřbitových oznaménovaných čísel je 7. Z hlediska čísel bez naménka je to ovšem operace dovolená.

Pro nás znamená typ integer 32 bitové číslo se znaménkem povolující uložení celého čísla v rozsahu –2 147 483 648 .. 2 147 483 647.
V případě, že nějaká oprace, např. v příkazu k:=i*j vede k přetečení, není obvykle spuštěn žádný poplach a program se posléze chová podivně bez zjevných příčin, protože výsledek přiřazovacího příkazu je jiný, než zamýšlený. Je ale možné donutit program, aby si tato možná přetečení ohlídal, stráví se tím nějaký čas navíc, ale ušetří to čas při hledání problémů. Až se budeme zabývat laděním programů bude zapnutí kontroly na přetečení jedním z bodů v návodu.

Ve vyjímečných případech budeme potřebovat vědět, že jsou k dispozici i jiné celočíselné typy:

Identif.Typu      Rozsah         Formát uložení
-----------------------------------------------
Shortint        –128..127        signed 8-bit
Smallint      –32768..32767      signed 16-bit
Longint  –2147483648..2147483647 signed 32-bit
Int64          –2^63..2^63–1     signed 64-bit
Byte               0..255        unsigned 8-bit
Word               0..65535      unsigned 16-bit
Longword           0..4294967295 unsigned 32-bit

Jak vidíme, typ Integer je v současné době totožný s typem Longint. Je pravděpodobné, že během několika let bude typ Integer odpovídat 64-bitovému číslu a neměli bychom spoléhat na to, že proměnné typu Integer jsou ukládány jako zrovna jako 32-bitové. Abychom však nemuseli hlídat každý součin 200*200 (nevejde se do SmallInt), budeme předpokládat, že těch bitů je nejméně 32, takže pozor na přetečení si budeme muset dávat až u součinů jako je 50000*50000.

S výjimkou typu Int64 obecně neplatí, že operace s kratším formátem je rychlejší, takže důvody pro použití kratšího formátu čísla musí být v algoritmu samém, ne jeho optimalizaci. Jednou z výjimek je úspora paměti při uložení miliónů a miliónů celých čísel v poli (viz dále), převážným důvodem ale bude respektování formátu vstupních dat: např. komponenty RGB v bitmapě jsou typu Byte, zvuk v audiosouboru na kompaktním disku je zase posloupnost dvojic (L,R) oznaménkovaných 16-bitových čísel ( typ SmallInt ).

Logické operace nad celými čísly

Z technických důvodů se čísla v počítači uskladňují ve dvojkovém zápisu. Na jednotlivé bity lze pak aplikovat logické operátory and, or, xor a not ve stejném smyslu jako pro true a false.

var x,y : Integer;

....

    x := 21;
    y := 12;

 { nyní platí }

    x or y = 29 
 { neboť

      00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
  or  00000000 00000000 00000000 00001100   // 12 =  0+8+4+0+0 
----------------------------------------------------------
      00000000 00000000 00000000 00011101   // 29 = 16+8+4+0+1    }

    x and y = 4
 { neboť

      00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
  and 00000000 00000000 00000000 00001100   // 12 =  0+8+4+0+0 
----------------------------------------------------------
      00000000 00000000 00000000 00000100   //  4 =  0+0+4+0+0 }

    x xor y = 25
 { neboť

      00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
  xor 00000000 00000000 00000000 00001100   // 12 =  0+8+4+0+0 
----------------------------------------------------------
      00000000 00000000 00000000 00011001   // 25 = 16+8+0+0+1 }

    not x = -22
 { neboť

 not    00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
---------------------------------------------------------------
        11111111 11111111 11111111 11101010   //-22 = (-1)-16-0-4-0-1  }

Mimochodem, aby si programátoři šetřili klávesy 0 a 1, místo binárního zápisu používají zápis šestnáctkový (hexadecimální). čtveřice bitů se podle výše uvedené tabulky ozačí číslicí 0..9 nebo písmenem A-F. Proto nám následující příkaz writeln vypíše TRUE:

writeln( not $15 = $FFFFFFEA );

Protože Wirth nepoužil znak $ ve své versi Pascalu, mohl být později použit $ jako uvozovací znak při zápisu šestnáctkového čísla a výše uvedený kód je správně.
Protože jde jen o zápis čísla pro kompilátor, a $15 je naprosto totéž jako 21, zkuste uhodnout co udělá následující příkaz:

writeln( $15 );

Rady do života: Celá a reálná čísla

V jazyce Pascal se přes jeho přísnou kotrolu typů povoluje použít celé číslo na místě reálného. Proto do reálné proměnné smíme dosadit hodnotu s typem Integer, přesněji v přiřazovacím příkazu
idProm:=Vyraz
kde idProm je identifikátor reálné proměnné smí mít Vyraz nejen reálný typ ale i typ celočíselný.

Ačkoili tedy nepředstavuje současné použití celých a reálných čísel v Pascalu problém, je v případě podílu dvou celých čísel na místě naučit se dávat si pozor. V příkazu

  E := 1/2*m*v*v;

se podíl 1/2 vyhodnotí na konstantu 0.5 a příkaz provede, co jsme zamýšleli. Protože však např. v jazycích FORTRAN a C se podíl 1/2 vyhodnotí jako 0 a do E se dosadí nula, je pro budoucího fyzika vhodné zvyknout si psát např.

  V := 4/3.0*Pi*r*r*r;

a nebo 4.0/3 atp. Nejjednodušší je nezvyknout, abychom si pak nemuseli odvykat.

Podobně bychom si neměli zvykat jako celočíselné ukládat hodnoty typu n! nebo 2^n neboť ani v 32-bitových celých číslech na ně není "dost místa".

Řešení problémů hrubou silou

Jako první při řešení nějakého problému uvažujeme algoritmus spočívající v použití hrubé síly.
Jako ilustraci tohot přístupu uvažujme následující program, který hledá všechny neuspořádané trojice kladných čísel, které leží na kouli o poloměru 2003, pokud je chápeme jako kartézské souřadnice bodu v prostoru a koule má střed v počátku.

Načtněme nejdříve obrysy takového postupu:

Pro všechny uspořádané trojice přirozených čísel které připadají v úvahu:
Zkontroluj, zda náhodou nesplňují zkoumanou rovnici
Pokud ano, vypiš výsledek.

Protože pro první bod nemáme k disposici odpovídající konstrukci jazyka Pascal, napíšeme jej podrobněji:
    1.1 Pro všechna čísla a od 1 do N-1
    1.2 Pro všechna čísla b od 1 do a
   1.3 Pro všechna čísla c od 1 do b

Teď již vidíme, že po překladu do "angličtiny" získáme kostru kódu, třeba takovýto:

program Rozklady1;

var a,b,c,N :integer;
begin
    N:=2003;
    Writeln('Rozklady cisla ',N);
    {pro vsechny trojice N>a>=b>=c>0 zkoumej zda plati}
    for a:=1 to N-1 do
      for b:=1 to a do
        for c:=1 to b do
          begin
            if a*a+b*b+c*c=N*N then writeln(a,' ',b,' ',c);
          end;

    Writeln('konec');
end.

Následující variantu je stále možné považovat za použití hrubé síly, i když je cca 60x rychlejší.

program Rozklady2;
var a,b,c,N :integer;
begin
  N:=2003;
  Writeln('Rozklady cisla ',N);
  {pro vhodne trojice N>a>=b>=c>0 zkoumej zda plati}
  for a:=1 to N-1 do
    begin
      b:=1;
      while (b<=a) and (N*N-a*a-b*b>0) do
        begin
          c:=trunc(0.5+sqrt(N*N-a*a-b*b));
          if (c<=b) and (a*a+b*b+c*c=N*N) then writeln(a,' ',b,' ',c);
          b:=b+1;
        end;
    end;
  Writeln('konec');
end.

Navíc se následujícími příkazy můžeme přesvědčit, že oba programy dávají stejné výsledky. Zde použijeme trik s přesměrováním výstupu programu do souboru (To je to znaménko > mezi příkazem a názvem výstupního souboru). Necháme tak vytvořit dva soubory, jejichž názvy si samozřejmě můžeme zvolit libovolně, a posléze jejich obsah porovnáme. Práci s porovnáváním obsahu můžeme přenechat počítači, pokud si zjistíme, který program to za nás udělá. Seznam takovýchto užitečných programů dodám později, a pak se dozvíte, že v tomto případě je třeba použít program s názvem FC (pro příkazový řádek MS Windows).

C:\Projects\prog\pokusy>Rozklady1 > Vysledky1.txt

C:\Projects\prog\pokusy>Rozklady2 > Vysledky2.txt

C:\Projects\prog\pokusy>fc Vysledky1.txt Vysledky2.txt
Comparing files Vysledky1.txt and Vysledky2.txt
FC: no differences encountered

C:\Projects\prog\pokusy>

Příkládky k přemýšlení
1. Jaké jsou typy následujících výrazů? Jsou všechny zapsány správně?

  {deklarace}
var i,j,k : integer;
    x,y,z : real;
       be : boolean;  

  { nyní následují výrazy }

    i+j
    i*j 
    i/j

    i+y
    i*y 
    i/y

    i mod y

be and i>j

i>j and x>y

be or not 2*be

2. Zapište jako přiřazovací příkazy následující vzorečky (volbu identifikátorů a počet přiřazení je na vás)

3. Doplňte do následujícího kódu správný výraz místo ?????

const N = 54354;
var i,j,k,pocetprocent: Integer;
begin
  {...}
  for i:=1 to N do
    begin
      {zkoumej moznost i}
        {...}
      {uz jsem to prozkoumal, ted to jeste oznamim obsluze, ktera ceka na vysledek}
      pocetprocent := ????? ;
      Write('Prave jsem prozkoumal ',pocetprocent,'% moznych hodnot.  ',#13);
    end;
  {...}
end.

Po správném doplnění otazníků můžete program použít jak je. Psaní hlášení o postupu výpočtu zabere programu tolik času, že vlastně ani není potřeba aby něco užitečného dělal a i tak poběží pár sekund. Vyzkoušejte !
Vyzkoumejte, co to je ten #13 !!! Třeba tak, že jej nejprve odstraníte, poté nahradíte třeba #33 a uvidíte ten rozdíl.

4. Všichni znáte součtové vzorce, zvažte následující kód:

const  k=100;
  alpha=0;
  beta=0.1;
 
var sa,ca,sb,cb,soucet : real;
     n:integer;
begin
     {do promennych sa a ca strcim sin prip cos alpha:}
 sa := sin(alpha);
 ca := cos(alpha);
     {do promennych sb a cb strcim sin prip cos beta:}
 sb := sin(beta);
  cb := cos(beta);
     { nyni mohu spocitat 
          soucet := sin(alpha)+sin(alpha+beta)+sin(alpha+2*beta)+...+sin(alpha+N*beta) ,
       kdyz vyuziji souctovych vzorcu takto:}

        soucet:=sa;
        for n:=1 to k do begin
    sa := sa*cb+ca*sb;
    ca := ca*cb-sa*sb;
          soucet := soucet + sa;
  end; 
        {...}
  writeln(soucet);
end.

Co je na tomhle kódu špatně? Přesněji, kde je v cyklu chyba, která způsobí, že nedostanu součet sinů? Opravte tu chybu.

Lekce 3

Aritmetické operátory a typy

Cím se liší následující výrazy?

    1*1
    1/1
    1>1

Operandy +-*/ mohou být čísla realná nebo celá, div a mod mají jako operandy pouze čísla celá.
Za předpokladu, že proměnné x,y,i a j jsou deklarovány takto:

  var i,j : integer; 
      x,y : real;

můžeme aritmetické oprace shrnout v následující tabulce

	význam	operand	výsledek	příklad--> typ výsledku
+	sčítání	real, integer	real,integer	x+i --> real
-	odčítání	real,integer	real,integer	i-j --> integer
*	násobení	real,integer	real,integer	x*y --> real
/	reálné dělení	real,integer	real	i/j --> real
div	celočíselné dělení	integer	integer	i div j --> integer
mod	zbytek při dělení	integer	integer	i mod j --> integer

Pro oparace +-* platí, že výsledek je celé číslo pouze pokud jsou oba operandy celá čísla.

Hodnota celočíselného podílu

   i div j

je rovna hdonotě reálného podílu zaokrouhlené směrem k nule, tedy

   i div j  = trunc(i/j)

Pro záporná i a/nebo j je tato definice kompatibilní se vztahy
(-i)/j = - (i/j), i/(-j) = - (i/j)

Operace mod splňuje vztah
i mod j = i – (i div j) * j

Obvukle ji budme používat pouze pro j>0 a i>=0, kdy platí že
i mod j = 0..j-1
tedy jde o běžnou operaci zbytku po dělení a např.
17 mod 5 = 2 .

Pokud je j=0, způsobí operace
x / j
i div j
i mod j
krach programu.

Unární oprátory + - nemění typ.

Logické operátory

  k :=  (i=imax) + (j=jmax);

( umožní nám to v budoucnu operace/funkce ord ).

Nad hodnotami false a true však pracují logické operátory:

1. Binární operátory: and, or, xor

and	false	true
false	false	false
true	false	true

or	false	true
false	false	true
true	true	true

xor	false	true
false	false	true
true	true	false

2. Unární operátor negace not:

not	false	true
	true	false

Relační operátory (=, <>, <, <=, >, >=)

Ve všech případech je výsledkem porovnání logická (boolean) hodnota.

Celá čísla v počítači

V současné době je standardem používat k uložení celého čísla 32 bitů. Protože je to docela dlouhé dvojkové číslo, použijeme pro následující příklad pouze čtyři bity.

Ilustrace

Do čtyřech bitů lze uložit následujících 16 kombinací 0 a 1:

3210   hex    unsigned     signed
----    -     --------     ------ 
0000    0        0            0  
0001    1        1            1
0010    2        2            2    
0011    3        3            3
0100    4        4            4    
0101    5        5            5
0110    6        6            6    
0111    7        7            7
1000    8        8           -8     
1001    9        9           -7 
1010    A       10           -6  
1011    B       11           -5  
1100    C       12           -4  
1101    D       13           -3      
1110    E       14           -2  
1111    F       15           -1

Protože pomocí 4 bitů můžeme reprezentovat čísla 0..15 resp -8..7 vedou některé operace k tzv. přetečení.

Ve vyjímečných případech budeme potřebovat vědět, že jsou k dispozici i jiné celočíselné typy:

Identif.Typu      Rozsah         Formát uložení
-----------------------------------------------
Shortint        –128..127        signed 8-bit
Smallint      –32768..32767      signed 16-bit
Longint  –2147483648..2147483647 signed 32-bit
Int64          –2^63..2^63–1     signed 64-bit
Byte               0..255        unsigned 8-bit
Word               0..65535      unsigned 16-bit
Longword           0..4294967295 unsigned 32-bit

Logické operace nad celými čísly

var x,y : Integer;

....

    x := 21;
    y := 12;

 { nyní platí }

    x or y = 29 
 { neboť

      00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
  or  00000000 00000000 00000000 00001100   // 12 =  0+8+4+0+0 
----------------------------------------------------------
      00000000 00000000 00000000 00011101   // 29 = 16+8+4+0+1    }

    x and y = 4
 { neboť

      00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
  and 00000000 00000000 00000000 00001100   // 12 =  0+8+4+0+0 
----------------------------------------------------------
      00000000 00000000 00000000 00000100   //  4 =  0+0+4+0+0 }

    x xor y = 25
 { neboť

      00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
  xor 00000000 00000000 00000000 00001100   // 12 =  0+8+4+0+0 
----------------------------------------------------------
      00000000 00000000 00000000 00011001   // 25 = 16+8+0+0+1 }

    not x = -22
 { neboť

 not    00000000 00000000 00000000 00010101   // 21 = 16+0+4+0+1
---------------------------------------------------------------
        11111111 11111111 11111111 11101010   //-22 = (-1)-16-0-4-0-1  }

writeln( not $15 = $FFFFFFEA );

writeln( $15 );

Celá a reálná čísla

Zvláštním případem je podíl dvou celých čísel. V příkazu

  E := 1/2*m*v*v;

  V := 4/3.0*Pi*r*r*r;

a nebo 4.0/3 atp.

Řešení problémů hrubou silou

Načtněme nejdříve obrysy takového postupu:

Pro všechny uspořádané trojice přirozených čísel které připadají v úvahu:
Zkontroluj, zda náhodou nesplňují zkoumanou rovnici
Pokud ano, vypiš výsledek.

program Rozklady1;

var a,b,c,N :integer;
begin
    N:=2003;
    Writeln('Rozklady cisla ',N);
    {pro vsechny trojice N>a>=b>=c>0 zkoumej zda plati}
    for a:=1 to N-1 do
      for b:=1 to a do
        for c:=1 to b do
          begin
            if a*a+b*b+c*c=N*N then writeln(a,' ',b,' ',c);
          end;

    Writeln('konec');
end.

Následující variantu je stále možné považovat za použití hrubé síly, i když je cca 60x rychlejší.

program Rozklady2;
var a,b,c,N :integer;
begin
  N:=2003;
  Writeln('Rozklady cisla ',N);
  {pro vhodne trojice N>a>=b>=c>0 zkoumej zda plati}
  for a:=1 to N-1 do
    begin
      b:=1;
      while (b<=a) and (N*N-a*a-b*b>0) do
        begin
          c:=trunc(0.5+sqrt(N*N-a*a-b*b));
          if (c<=b) and (a*a+b*b+c*c=N*N) then writeln(a,' ',b,' ',c);
          b:=b+1;
        end;
    end;
  Writeln('konec');
end.

C:\Projects\prog\pokusy>Rozklady1 > Vysledky1.txt

C:\Projects\prog\pokusy>Rozklady2 > Vysledky2.txt

C:\Projects\prog\pokusy>fc Vysledky1.txt Vysledky2.txt
Comparing files Vysledky1.txt and Vysledky2.txt
FC: no differences encountered

C:\Projects\prog\pokusy>

Příkládky k přemýšlení
1. Jaké jsou typy následujících výrazů? Jsou všechny zapsány správně?

  {deklarace}
var i,j,k : integer;
    x,y,z : real;
       be : boolean;  

  { nyní následují výrazy }

    i+j
    i*j 
    i/j

    i+y
    i*y 
    i/y

    i mod y

be and i>j

i>j and x>y

be or not 2*be

2. Zapište jako přiřazovací příkazy následující vzorečky (volbu identifikátorů a počet přiřazení je na vás)

3. Doplňte do následujícího kódu správný výraz místo ?????

const N = 54354;
var i,j,k,pocetprocent: Integer;
begin
  {...}
  for i:=1 to N do
    begin
      {zkoumej moznost i}
        {...}
      {uz jsem to prozkoumal, ted to jeste oznamim obsluze, ktera ceka na vysledek}
      pocetprocent := ????? ;
      Write('Prave jsem prozkoumal ',pocetprocent,'% moznych hodnot.  ',#13);
    end;
  {...}
end.

4. Všichni znáte součtové vzorce, zvažte následující kód:

const  k=100;
  alpha=0;
  beta=0.1;
 
var sa,ca,sb,cb,soucet : real;
     n:integer;
begin
     {do promennych sa a ca strcim sin prip cos alpha:}
 sa := sin(alpha);
 ca := cos(alpha);
     {do promennych sb a cb strcim sin prip cos beta:}
 sb := sin(beta);
  cb := cos(beta);
     { nyni mohu spocitat 
          soucet := sin(alpha+beta)+sin(alpha+2*beta)+...+sin(alpha+N*beta) ,
       kdyz vyuziji souctovych vzorcu takto:}

        soucet:=sa;
        for n:=1 to k do begin
    sa := sa*cb+ca*sb;
    ca := ca*cb-sa*sb;
          soucet := soucet + sa;
  end; 
        {...}
  writeln(soucet);
end.

Co je na tomhle kódu špatně? Přesněji, kde je v cyklu chyba, která způsobí, že nedostanu součet sinů? Opravte tu chybu.

Procedury a funkce

Čím je kód programu vzdálenější našemu jazyku, tím větší je pravděpodobnost, že při psaní kódu programu uděláme chybu. Platí to i u intelektuálně nenáročných kusů kódu: Při psaní

y := ln(x + sqrt(x*x + 1))

ještě nejspíš chybu neuděláme, i když zápis

y := ArcSinh(x)

je přehlednější a mnohem odolnější vůči chybě. Pokud budeme chtít spočíst

z := ArcSinh(sqrt((x-1)/(x+1)))

roste pravděpodobnost, že se při přepisu do tvaru

z := ln( sqrt( (x-1)/(x+1) ) + sqrt( 2*x/(x+1) ) )

dopustíme chyby.

Pododbně jako výpočet nějaké funkce může nějaká posloupnost příkazů tvořit jasný celek, který je pak pro přehlednost možné vyjmout z místa, kde jej chceme uplatnit a vytvořit z něj Proceduru.

Satrapa [Sa] píše:

Kdykoli si řeknete "teď by se mi hodilo aby pascal měl příkaz (nebo funkci), který ....", vymyslete si vhodné jméno a obohaťte Pascal o nový příkaz (či funkci) - definujte podprogram.

Uvidíme, že budou případy, kdy to takto jednoduše nepůjde, ale jako motto je to výstižné.

I když jsme se vzdali představy, že o budeme dokazovat správnost programu, nepochybně chceme psát správné programy. Vytvořením vhodné hierarchie krátkých přehledných podprogramů, lze i ideálním případě na každé úrovni dosáhnout toho, že na každé úrovni je podprogram očividně správně.

Ovšemže by měl být zmíněn také hlavní a každému zřejmý důvod zavední procedur a fukcí: V případě, kdy bych byl nucen opakovat již jednou napsaný kus kódu, nabízí se tu možnost ulehčit si práci se psaním. Protože jsme ze školy zvyklí myslet "strukturovaně", oba důvody pro použití funkcí (a procedur) se překrývají: Kód se opakuje, protože representuje nějaký podproblém.

Euklidův algoritmus jako funkce

Jako příklad budiž zmíněn opět Euklidův algoritmus. Co kdybychom chtěli spočíst nějvětší společný dělitel tří čísel? Jak? Co takhle spočíst NSD třetího čísla a NSD prvních dvou čísel? ..... Pak by zřejmě nebylo od věci moci zapsat celý postup třeba takto:

vysledek := GCD( c, GCD(a,b) );

Aby nám překladač rozumněl, musíme mu oznámit, že
1.   GCD je identifikátor funkce
2.   funkce GCD má dva celočíselné parametry
3.   funkce GCD vrací jako výsledek celé číslo
4.   Aby to fungovalo, musíme také říci jak se má ze vstupních
      hodnot vyrobit výsledek (jakýsi malý program).

V jazyce Pascal se to provede tak, že v deklaracích bloku, ve kterém chceme tuhle funkci použít, spolu s proměnnými a konstantami, deklarujeme ještě fukci.

   function GCD(a,b : integer) : integer;
   var c:integer;
   begin
     repeat
        c := a mod b;
        a := b;
        b := c; { (a,b) := (b,a mod b); }
     until b=0;
     GCD := a;
   end;  {function GCD}

Časem si nakreslíme syntaktický diagram, ale i bez něj rozpoznáváme jasnou strukturu Hlavička-Deklarace-Složený Příkaz, jakou má pascalský program. Z kódu je jasně vidět, že použití identifikátorů a,b se neodlišuje od použití identifikátoru proměnné c. Na rozdíl od proměnných mají ale a a b na začátku přiřazené hodnoty. Pokud bychom funkci GCD použili například takto:

   n := GCD(44,55) ;

bude na začátku provádění příkazů těla funkce mít a hodnotu 44 a b hodnotu 55. Proměnná c bude mít hodnotu nedefinovanou. Proto její hodnota nesmí být užita dříve, než jí bude nějaká přiřazena.

Takto pak vypadá celý kód programu:

program GCD3;

const a = 26112;
      b = 75548;
      c = 45288;

var   n : integer;

function GCD(a,b : integer):integer;
   {Vrací NSD dvou kladných čísel}
   var c:integer;
   begin
     if (a<=0) or (b<=0) then {oznam chybu a skonci}
     begin
        Writeln('Funkce GCD(', a, ',', b, ') : Neplatne parametry!');
        Halt;
     end;

     repeat
        c := a mod b;
        a := b;
        b := c;
     until b=0;
     GCD := a;
   end;  {konec deklarce funkce GCD}

begin
   n := GCD( a, GCD(b,c) ) ;

   Writeln('Nejvetsi spolecny delitel cisel ', a,' ',b,' ',c,' je ',n,' nebot:');

   Writeln(a,' = ',a div n,'*',n);
   Writeln(b,' = ',b div n,'*',n);
   Writeln(c,' = ',c div n,'*',n);

   Readln;
end.

Co se děje při použití procedury či funkce

Co se děje, když se provádí příkaz n := GCD(44,55) ? Je na překladači, zda to pochopí tak, že sem má "zkopírovat" náš kód pro NSD (tzv. makro/inline), nebo zda použije mechanismus volání podprogramu. Ten můžeme přirovnat k vyplnění žádanky byrokratem samotářem: Do kolonky a si napíše 44, do kolonky b 55. Pak si ještě vyplní kolonku s poznámkou, kde má pokračovat až se dozví výsledek. Poté nalistuje stranu v manuálu pro GCD a tam se přesně dozví co má s žádenkou dělat. Až nakonec nalezne výsledek, podívá se do kolonky kam se má vrátit, nalistuje příslušnou stránku a pokračuje. Takto se až na výjimky překládají funkce a procedury.

Vezměme jako příklad program P s funkcí f

program P;
function f(a:real):real;
begin
  f:=sin(a)
end;

begin
  writeln(f(1));
  writeln(f(2));
end.

Otázka pak zní zda se program přeloží do kódu


   VezmiKonstantu 1.0   
   SpočtiSinus  
   VypišHodnotu
   VezmiKonstantu 2.0   
   SpočtiSinus  
   VypišHodnotu
   Skonči

nebo do kódu

   VezmiKonstantu 1.0   
   ZavolejFunkci f  
   VypišHodnotu
   VezmiKonstantu 2.0   
   ZavolejFunkci f  
   VypišHodnotu
   Skonči
TadyJeFunkce f:
   VyzvedniPředanouHodnotu
   SpočtiSinus  
   VraťSe

Vidíme že druhá varianta je v tomto případě delší, ale tušíme, že pokud by funkce f byla komplikovanější, zabraly by její dvě(či ještě více) kopie více místa než vyžaduje varianta druhá. Tušíme, že první varianta (hantýrka: macro nebo též inline) je výhodná pouze pro extrémně krátké funkce a běžně se stává, že ji kompilátory vůbec nepodporují. Měli bychom tedy vědět, že funkce a procedury se překládají jako samostatné kusy programu a jejich kód je uložen i velmi daleko od místa, kde se používají.

Poznámka: ve starém hrozném BASICu to bylo jasné, protože jediný způsob jak volat proceduru se jmenoval GOSUB, jdi na podprogram a každý tak viděl, že volání proceduru je nějaký vylepšený příkaz GOTO.

Procedury jako nástroj strukturovaného programování

Procedury na rozdíl od funkcí, nevracejí hodnotu, přesněji nepoužíváme je ke konstrukci výrazů, ale jsou to příkazy. Pomáhají nám, aby naše programy mohly být složeny z přehledných částí. Třeba takto:

Program VylepsovacZvuku;
..... 
begin
  NactiAudiosoubor;
  OpravPraskani;
  SnizSumeni;
  ZapisAudiosoubor;
end.

Teď už jen zbývá napsat ty čtyři procedury. Každou z nich napíšeme jako posloupnost dostatečně jednoduchých operací, a pokud nebudou v nabídce jazyka Pascal, vymyslíme vhodný identifikátor nové procedury, která tuto složitou operaci zařídí a tuto posléze stejným postupem rozepíšeme jako posloupnost ještě jednodušších příkazů. Takže psát programy je jednoduché, že.

Toto je velmi zhruba idea psaní program shora dolů. Je dobré ji mít na paměti, když program píšeme, jakkoli nám nebude při psaní programu vždy pasovat na naši úlohu. V každém případě stála u kolébky globální struktury jazyka Pascal jak uvidíme v následujícím:
Připomeňme si nejprve syntaktický diagram pro program:

A takto vypadají diagramy pro proceduru a funkci

Jak vidíme jsou procedury složeny kromě hlavičky opět z bloku a v něm můžeme kromě proměnných a konstant deklarovat i opět další procedury a tak by náš program mohl vypadat takto:

Program VylepsovacZvuku;
...
   Procedure OpravPraskani;
   ...
      Procedure OdectiPoruchu;
      ...
      begin
        ...
      end;
   ...
   begin
     ...
     OdectiPoruchu;
     ...
   end;
...
begin
  ...
  OpravPraskani;
  ...
end.

Procedura OdectiPoduchu se nachází uvnitř jiné procedury a ne programu, říkáme, že je to vnořená procedura (funkce). Upozornění: vnořené procedury (a funkce) nejsou v některých běžných programovacích jazycích podporovány, takže pokud si na ně příliš zvykneme hrozí nám dalším životě riziko, že si budeme muset odvykat.

Procedury a funkce mají své proměnné

Přesněji bychom měli mluvit o identifikátorech, protože v deklarační části procedury a funkce můžeme deklarovat cokoli, co můžeme deklarovat v bloku programu, proměnné jsou ale tím nejdůležitějším.

Abychom mohli používat podprogramy, je třeba vyjasnit které identifikátory platí uvnitř kterého bloku. Veměme třeba

program KdoKdyKde;

var N,i,s:integer;

  function f(a:integer):integer;
  var i,s:integer; {co kdyz tenhle radek zakomentujeme ?}
  begin
    s:=0;
    for i:=1 to N do s:=s+sqr(a+i);
    f:=s;
  end;

begin
  N:=10;
  s:=0;
  for i:=1 to N do s:=s+f(i);
  writeln(s);
  readln;
end.

Když někde v bloku deklarujeme identifikátor, zůstává v platnosti až do konce tohoto bloku. Může však být zakryt deklarací uvnitř bloku nějaké funkce či procedury. To je případ identifikátorů i a s uvnitř funkce f v příkladu výše. Naopak, proměnná N je viditelná i uvnitř funkce f (není ničím zastíněna), čehož využíváme. Proměnné deklarované v bloku programu naýváme globální, ty deklarované v bloku procedury či funkce nazýváme lokální.
Identifikátor je definován počínaje nejbližžším středníkem po jeho deklaraci a konče endem složeného příkazu bloku v němž je deklarován.

Pozor, lokální proměnné nejen že nejsou vidět za endem bloku kde byly deklarovány, ale ani místo v paměti pro ně není přiděleno, když kód procedury zrovna "neběží". Není tedy možné si v nich schovávat hodnoty mezi dvěma voláními téže funkce.

Parametry procedur

Především můžeme hodnoty předávat prostřednictvím společných (tedy většinou globálních) proměnných .

program ProcSGlobProm;

var i;

  procedure MojeProc;
  begin
     i:=0;
  end;

begin
  i:=1;
  Writeln(i);
  MojeProc; 
  Writeln(i);
end.

Pak můžeme použít parametry funkce. Nejjednodušším případem je tzv. předání hodnotou.

program ProcSParHodnotou;

var i;

  procedure MojeProc(b:integer);
  begin
     b:=0;
  end;

begin
  i:=1;
  Writeln(i);
  MojeProc(i); 
  Writeln(i);
end.

V tomto případě mi program vypíše dvě jedničky. Procedura se dozví jakou hodnotu mělo i, ale dále pracuje jen s touto hodnotou. Proměnné b přísluší vlastní chlívek v paměti a jeho modifikací se nemění hodnota chlívku i.

Nyní jak vypadá předání parametru odkazem

program ProcSParOdkazem;

var i;

  procedure MojeProc(var b:integer);
  begin
     b:=0;
  end;

begin
  i:=1;
  Writeln(i);
  MojeProc(i); 
  Writeln(i);
end.

V tomto případě mi program vypíše jedničku a nulu. Procedura se dozví kde je uskladněna proměnná i, a dále pracuje s tímto odkazem, tedy s proměnnou samou. Předání parametru odkazem zařídí, že chlívek s názvem i se uvnitř procedury jmenuje ještě též b.

[Tady zatím nemám sílu vymýšlet jak sem přepsat to povídání o chlívcích a odkazech, kdyby se někomu chtělo napsat javascriptovou animaci, uvítám to... ]

Předávání odkazem je tak možné použít i k navrácení hodnoty tam, kde je použití funkce nevhodné.
Především funkce neumí pohodlně vrátit dvě hodnoty zároveň. Často se také používají funkce var parametry na návrat hodnot, zatímco funkce sama vrací jen logickou informaci, zda se to povedlo:

  function NactiSeznam(var Sz : typSeznam; JakDlouhy : integer) : boolean;
  begin
     ....

     ....
     NactiSenznam := NacenaDelka = JakDlouhy;
  end;

Ještě se o tom zmíníme, ale je třeba uvést, že kromě použití var-parametrů pro návrat hodnoty, je další indikací pro použití var-parametrů velikost předávaných dat. Náročnost předání odkazu je totiž nezávistlá na velikosti toho na co odkazuji.

Pravidla a dokumentace

Procedury a funkce tvoří nejdůležitější prvek, který používáme při členění programu. Je dobré, když při jejich psaní dodržujeme jistá pravidla. Především u funkce či procedury rozlišujeme:
1. Co od nás chce
2. Co nám vrátí
3. Co kromě toho udělá

Funkce sqrt od nás požaduje nezápornou hodnotu parametru, pak nám vrátí jeho odmocninu (s nějakou zaručenou přesností) a neudělá nic dalšího! Nepípá na nás, nevypisuje 'cekejte pocitram odmocninu', nemění přesnost s níž se provádějí výpočty (i to lze někde měnit) an nic jiného, jen odmocňuje!
Jiný příklad: procedura VypišSeznam ... nemá žádné požadavky na seznam, nic nám nevrátí a neudělaá nic jiného, než že seznam vypíše. Nemění ho, nepřidává položku. Nemá vedlejší účinky.
Pokud to jde píšeme takovéto čistokrevné procedury a funkce.
Často jsou ale naše procedry a funkce komplikované, pracují jen někdy (bod 1), vrací nám něco (bod 2) a zárověň ještě navíc něco provedou (bod 3). Protože je pak při větším rozsahu programu těžké pamatovat si všechny tyto informace, je vhodné všechny tři body dokumentovat. Jinak řečeno pokud od nás funkce něco chce, musíme si to poznamenat dokud si to pamatujeme. Pokud identifikátor funkce neříká jasně, co fuknce vrací či procedura dělá, přidáme komentář. A pokud funkce má ještě nějaké vedlejší účinky nesmíme zapomenout se o nich zmínit v komentáři. Podobně pokud procedura něco vrací, což od ní většinou nečekáme, nezapomeneme na komenář. Ten pak umístíme co nejblíže hlavičce procedury či funkce.
Jazyka Pascal nespecifikuje jak má takový komentář vypadat, chcete-li se nechat inspirovat podívejte se do nějaké učebnice jazyka Java, tam to všechno je.

Malujeme funkci

Naše znalosti nám začínají umožňovat psát užitečné programy a díky možnosti dát programu strukturu můžeme jednou nalezená řešení znovu použít.

Nejdříve si ukažme, jak můžeme namalovat graf funkce.

program MalujFci;

const xa = 0;
      xb = 1;
      N  = 100;

function MalovanaFce(x:real):real;
begin
  MalovanaFce := x*exp(x)
end;

var x,y : real;
      i : integer;

begin
  for i := 0 to N do begin
    x := xa + (xb-xa)*i/N;
    y := MalovanaFce(x);
    writeln(x,' ',y);
  end;
end.

Především si všimněme, že zde je malovaná funkce izolovaná do zvláštní funkce a příkazy těla programu se výpočtem funkční hodnoty nezabývají. Sice jsme si tím program trochu zkomplikovali, ale až budeme chtít malovat jinou funkci, bude nám identifikátor funkce připomínat, kde je třeba program změnit.

I při letmém prohlédnutí kódu ovšem okamžite vidíme, ze program nic nemaluje, pouze vypíše tabulku skládající se ze dvou sloupečků oddělených mezerou. V prvním je hodnota nezávislé proměnné, ve druhém funkční hodnota. Proč se tedy tady mluví o malování fukce?

Pokud bychom měli "namalováním grafu funkce" na mysli zobrazení grafu na obrazovce počítače a posléze toho i dosáhli, brzy bychom došli k názoru, že si ten obrázek ještě chceme uložit. Po chvíli bychom pak pak zjistili, že nejmenší omezení pro budoucí práci s obrázkem dosáhneme, pokud si poznamenáme funkční hodnoty namalované funkce pro případ, že bychom si chtěli prohlédnout detailní chování funkce v okolí nějakého bodu nebo místo lineárního zvolit logaritmické škálování os, atp. Proto si necháváme otevřené všechny moznosti, a jednoduše vypisujeme pouze funkční hodnoty.

Aby data jentak "nezmizela" za horním okrajem okénka konsole, provedeme trik, který jsme jiz použili: přesměrujeme výstup programu do souboru. Možná si ješte pamatujete, že se to dělá tak, že na příkazové řádce kromě spuštení programu požádáme též o přesměrování uvedením znaku '>' a názvu souboru:

C:\Projects\prog\pokusy>MalujFci > graf1.dat

To ale znamená, že budme potřebovat něco, co nám z hodot uložených v souboru graf1.dat udělá obrázek. Na počítaci se takové něco nazývá obecně program a jak to s programem bývá není nad to, když uz někdo takový program napsal a dovolí nám ho používat.

Malujeme funkci - GNUPLOT

Pro naše potřeby bude ideální program s názvem gnuplot (a jak nám napovídají první písmena názvu, nebudeme za něj muset nic platit). Uživatel ovládá gnuplot prostrednictvím príkazů. Například soubor, který se skládá ze dvou sloupců čísel vykreslíme jako graf funkce tak, že zadáme příkaz

plot "graf1.dat"

bouhužel takto ješte nezískáme, co chceme, protože nám vyleze graf složený z puntíků.

Proto budeme chtít program přesvedčit, aby maloval data ze souboru pomocí čar. Máme dvě moznosti. Buď k příkazu plot přidáme na konec "with lines", tedy

plot "graf1.dat" with lines

nebo změníme nastavení pomocí příkazu set a pak uz můžeme jen poroučet plot, plot, ....

set data style lines
plot "graf1.dat"

K jednou zadanému příkazu se můžeme vracet pomocí kláves [nahoru] a [dolu], takze se nemusíme opakovaně obtěžovat s vypisováním názvu datového souboru.

Budeme-li chtít vykreslit do jednoho grafu data ze dvou souborů jendoduše názvy souboru v úvozovkách oddělíme čárkou

plot "graf1.dat", "graf2.dat"

Konečně, pokud má soubor tvar tří (nebo více) sloupečků čísel, můžeme nechat vymalovat nejdřív první versus druhý sloupec hodnot a poté první versus třetí sloupec následujícím příkazem:

plot "graf2.dat", "graf2.dat" using 1:3

jak je vidět, using 1:2 jsme psát nemuseli, to se rozumí samo sebou.

Program gnuplot si podle rozsahu malovaných hodnot sám určí v jakém rozsahu se mají oškálovat osy. Pokud ale chceme některou z takto určených hodnot změnit, můžeme hned za slovo plot přidat meze v hranatých závorkách oddělené dvojtečkou. Vyzkoušejte, co udělají následující příkazy:

plot [0.2:0.5] "graf1.dat"
plot [:0.5] "graf1.dat"
plot [0.2:] "graf1.dat"
plot [][0:10] "graf1.dat"
plot [0.2:][:10] "graf1.dat"

Časem budeme potřebovat vědět, že pokud v datovém souboru vynecháme prázdný řádek, chápe gnuplot následující data jako novou křivku, pokud vynecháme dva prázdné řádky, chápe data jako rozdělená na sekce, přičemž můžeme s jednotlivými sekcemi pracovat zvlášť pomocí slova index.To použijeme později, taď jen je dobré vědět, že když potřebujeme znát správné použití třeba slova index, napíšeme: help index. Dále je dobré vědět, že až budeme potřebovat obrázek začlenit do nějakého článku, nabídne nám gnuplot možnost vytvořit obrázek v moha ruzných formátech (mimo jiné jako postscriptový soubor pro úcely publikace v knize ci časopise a png-soubor (případně gif) pro zveřejnění grafu na "webu"). Samozřejmě, stačí napsat help postscript případně help png či help gif a dozvíme se jak na to.

Jak asi začíná být zřejmé, program gnuplot nám v přednášce postačí pro běžné malování křivek a pro svoji jednoduchost a pružnost se vám nejspíš stane uzitečným pomocníkem i v následujících letech . Až budeme ovšem v přednášce hovořit o 2D grafice a budeme místo průbehu funkcí třeba vybarvovat trojúhelníky, použijeme jinou metodu.

Matematické fukce

Podle toho, že v Pascalu máme zdarma tak málo matematických funkcí (abs, sqr, sqrt, sin, cos, arctan, exp a ln) by jeden mohl hádat, že Wirth měl aversi k matemtické analýze. Pravděpodobne ale jde o důsledné uplatnění principu jednoduchosti. Protože prehršle různých funkcí znamenala nezbytně prodloužení manuálu a právě nepřehlednost jazyků té éry, byla tím, co informatici generace autora Pascalu velmi kritizovali. Osud jazyka PL/I napovídá, že nejspíš měli v něčem pravdu.

Znamená to snad, že se tedy např. máme navždy smírit s absencí funkce ArcSin v Pascalu? Protože víme, že mužeme definovat nové funkce, je odpoved jasná: definujeme funkci ArcSin:

function ArcSin(sinus : real) : real;
{ spocte uhel, jehoz sinus zname }
var cosinus: real;
begin
  cosinus := sqrt(1-sqr(sinus)); {bereme vzdy znamenko +sqrt(...)}
  if cosinus=0 then if sinus>0 then ArcSin := Pi/2
                               else ArcSin := -Pi/2  
               else ArcSin := ArcTan( sinus / cosinus );
end;

A je to! Za povšiknutí stojí, že výpočet se zhroutí pokud bychom chtěli počítat arcusinus arumentu v abolutní hodnotě větší než jedna.

Řady

Často jsou funkce dány ve formě mocninné řady. Vezměme třeba následující vzorec pro výpočet obvodu elipsy:

Tento vzoreček si říká o přímočarý přepis. Jedinou otázkou je jak dlouho řadu sčítat. Budeme předpokládat, že řada konverguje dostatečně rychle, takže ukončení rady členem nějaké velikosti znamená chybu ve výpoctu stejného rádu (viz dále). V okamžiku, kdy tento předpoklad neplatí, není řada vhodná pro sčítání a musíme nalézt jinou formulku [Jarník Integrání pocet II].

function ObvodElipsy(a,b : real) : real;

const posledni = 1E-12;

var epsilon,
    s,ds,f2: real;
    k      : integer;

begin
  epsilon := sqrt(a*a-b*b)/a;
  s  := 1;
  k  := 1;
  f2 := 1;  {sqr(1*3*5*.../(2*4*6*...))*eps^2k}
  repeat 
    f2 := f2*sqr((k+k-1)/(k+k)*epsilon);
    ds := f2/(k+k-1);
    s  := s-ds;
    k  := k+1;
  until ds<posledni;

  ObvodElipsy := 2*Pi*a*s;
end;

Všimněte si postupu obvyklého u takovéhoto typu sčítání řad. Obecně se snažíme provádět uvnitř cyklu co nejméně operací, a protože lze většinou jednoduše k-tý koeficient odvodit z toho předchozího, není potřeba do cyklu sčítání vkládat ještě cyklus počítající všechny ty součiny. (Puntičkář by možná ještě odstranil dělení v přirazení ds := f2/(k+k-1) ). Daleko důlezitejší neř pár zbytecných operací je ovšem vědět, v jakémrozsahu parametrů se na funkci můžeme spolehnout. To je ovšem především záležitost matematické analýzy. Pokud má funkce jednoduchou formu závislosti na parametrech lze ale chování "naprogramované" funkce ověřit. Pro představu je na ásledujícím obrázku závistlost relativní chyby výsledku volání funkce ObvodElipsy(1,x) na velikosti vedlejší poloosy. Pripomeňme si, že jsme zvolili const posledni = 1E-12; a vzhledem k přesnosti zvolené metody bychom asi měli nekam do kódu přidat varování, pokud podíl parametrů b/a není dostatecne velký.

Námět na přemýšlení: jak získat data potřebná pro určení chyby metody, když nemáme po ruce přesné hodnoty s výjimkou b=a a b=0, tedy kruznice a úsecky?

Rekurentní vztahy

Nejjednodušším příkladem je samozřejmě funkce faktoriál:.

n! = n (n-1)!
0! = 1

Jiným standardním příkladem je Fibonacciho posloupnost:

F(n) = F(n-2)+F(n-1)
F(0) = 0
F(1) = 1

Jakkoli je nasnadě použít pro výpočet prostředky rekurse jazyka Pascal, nebudeme je v toěchto případech používat. Programová rekurse je znázorněna pro faktorial takto:

a odpovídá následujícímu kódu:

function faktorial(a:integer):real; 
begin   
  if a<=1 then faktorial := 1          
          else faktorial := a*faktorial(a-1); 
end;

Pro Fibonacciho posloupnost takto

kde je nevhodnost programové rekurse naprosto zřejmá.
Cvicení: Vyzkoušejte si napsat rekurentní versi funkce Fibonacci(n : integer).
Cvicení: Kolikrát se zavolá funkce Fibonacci, kdyz se takto pokoušíme spočíst Fibonacci(6)?

Jak tedy převedeme matematický rekurentní vztah na návod pro počítač? Nejjednodušší je samozrejme případ funkce faktorial

function faktorial(a:integer):real;
var i : integer;
       s : real
begin
  s:=1;
  for i:=2 to a do s := s*i;
  faktorial := s;
end;

Takto zapsaný postup má jediný háček: vrací rozumnou hodntu i pro záporné hodnoty parametru a. Podobně jako by nebylo nejlepší, kdyby nám sqrt vracelo nulu pro záporné parametry (dáváme přednost krachu programu), měli bychom přidat test na záporné hodnoty a a program případně ukončit.
Cvičení: Zkuste na cyklus prevést výpocet funkce Fibonacci.

Zde si ukázeme, jak převést na cyklus složitější variantu Fibonacciho vztahu. Zadání, které nalezneme v učebnici fyziky zní:

kde Pn(x) je tzv. Legendreuv polynom a během studia jej mnohokrát potkáte. Pro nás je úloha omezena na nalezení hodnoty Pn(x) pro dané celé n>=0 a reálné x. Jak je vidět, je potřeba rozlišit případy n=0, n=1 a zbytek, kdy použijeme uvedenou formulku opakovaně (n-1)-krát. Zde je jedna z variant:

function LegendreP( m : integer; x : real ) : real;
var Pn2, Pn1,Pn : real;
              n : integer;
begin
   Pn := 1; {P0(x)}
   if m = 1 then Pn := x; {P1(x)}
   Pn2 := 1;
   Pn1 := x;
   for n := 2 to m do begin
      Pn := ((n+n-1)*x*Pn1 - (n-1)*Pn2 )/n;
      Pn2:= Pn1; {Pn->Pn1->Pn2}
      Pn1:= Pn;
   end;
   LegendreP := Pn;
end;

Příkaz cyklu for se nám postará o zvyšování n od 2 až do m, ale s každým zvýšením hodnoty n je potřeba také posunout hodnoty v proměnných, které si "pamatují" hodnoty Pn-2 a Pn-1.

Pro vykreslení použijeme následující program

program MalujLegendreovyPolynomy;

const xa = -1;
      xb = 1;
      N  = 400;

function LegendreP( m : integer; x : real ) : real;
...... viz výše ....

var k,i : integer;
    x,y : real;

begin
  for k := 0 to 12 do begin
    for i := 0 to N do begin
      x := xa + (xb-xa)*i/N;
      writeln(x,' ',LegendreP(k,x));
    end; {graf pro pevne x}
    writeln; {vypiš dva prázdné rádky}
    writeln;
  end; {dalsi k}
end.

Ten vypíše tabulku hodnot Funkce P0(x), poté dva prázdné řádky, pak tabulku hodnot funkce P1(x), pak dva prázdné řádky atd. až nakonec tabulku funkčních hodnot P12(x). Zadáme-li programu guplot příkaz plot "legendre.dat", kde soubor legndre.dat obsahuje výstup našeho programu, dostaneme následující obrázek

Protože jsme ale oddělili jednotlivé tabulky hodnot dvěma prázdnými řádky, můžeme si z toho zmatku vybrat jen ty křivky, které nás zajímají a to pomocí slova index následujícího za názvem datového souboru. Např.

plot "legendre.dat" index 1,"legendre.dat" index 2,"legendre.dat" index 3, "legendre.dat" index 12

nám vymaluje tabulky hodnot polynomu P1, P2, P3 a P12. Ještě se k tomu vrátíme v povídání o polích, ale je dobré vědet, že první sekci dat odpovídá index 0 a tak shodou okolností se index sekce shoduje s řádem Legendreova polynomu.

Pozor: někdy se může stát, že rekurentní vztah podobný výše uvedenému pro Legendrovy polynomy nefunguje, neboť s rostoucím n může do závratných výšek narůst úplně drobná počátecní nepřesnost. Diskuse tohoto jevu je ovšem mimo možnosti této prednášky.

Polynomy ( Hornerovo schéma )

Protože nás matematici učí, že spojité funkce můžeme aproximovat polynomy, často mají počítané funkce tvar polynomů. Následující funkce počítá s relativní chybou pod 1E-12 obvod elipsy. Hodnoty koeficientů polynomu samozřejmě spadly s nebe (od pana Čebyševa).

function ObvodElipsyP(a,b : real):real;
var x : real;
begin
  x := sqrt(a*a-b*b)/a; {epsilon}

  if x>0.5 then
  begin
    Writeln('Pouzivam aproximaci platnou do vystrednosti 0.5! ale chce se po me:',x);
    Halt;
  end;

  x := (((((((((((-0.7447687857522e-1*x+0.1590001893248)*x-0.1740344498264)*x+0.1042163635809)
       *x-0.5263574825627e-1)*x+0.1129877259030e-1)*x-0.2157908636362e-1)*x+0.2458101342560e-3)
       *x-0.4689377871622e-1)*x+0.8483390673316e-6)*x-0.2500000198143)*x+0.1811318676024e-9)*x+0.9999999999997;

  ObvodElipsyP := 2*Pi*a*x;
end;

Za povšimnutí stojí jen způsob, jímž je polynom vyčíslován. Vidíme, že se nikde nemusí počítat bůhvíjaké mocniny x, vše vyřešil Mgr. Horner pomocí závorek a celé se to po něm jmenuje Hornerovo schéma.

Iterační algoritmy (zatím pro hledání kořenů)

Tvoří velmi důležitou třídu algoritmů. Povětšinou spočívají v aplikaci zázračné formulky, která říká jak z méně přesného výsledku vyrobit výsledek přesnější a jejím opakování až do dosažení požadované přesnosti. Zde si ukážeme jak několik takových formulek a algoritmů na nich založených.

Půlení intervalu

Nabývá-li spojitá funkce v bodě a zápornou a v bodě b kladnou hodnotu, musí se nejméně jeden kořen funkce nacházet někde mezi těmito dvěma hodnotami. Zkusíme-li uprostřed spočíst funkční hodnotu uprostřed intervalu v bodě c=(a+b)/2 buď rovnou nalezneme kořen, nebo nalezneme kratší podinterval, ve kterém se kořen zaručeně nachází. Podle znaménka c je to buď <a,c> nebo <c,b>. Pokud je tento podinterval ještě stále moc velký, celý postup opakujeme. Délky intervalů tvoří geometrickou posloupnost s kvocientem 1/2. Proto každých deset iterací přidá tři desetinná místa a po 52 iteracích dosáhneme přesnosti s níž je uložena neznámá, pokud uvažujeme, že jsme začali s intervalem <1,2>. Pokud bychom se na reálnou proměnnou dívali ve dvojkovém zápise, dá se zhruba říci, že v každém kroku iterace přidáme jeden bit přesnosti. Toto je nejpomalejší metoda hledání kořene ale musíme ji ovládat. Pokud totiž máme dost času a nebo je funkce do té míry ošklivá, že rychlejší metody nemůžeme použít, je rozumné použít půlení ntervalu pro jeho spolehlivost.

Newtonova metoda

Na rozdíl od půlení intervalu, vyžaduje newtonova metoda, aby poblíž kořene byla funkce dostatečne hladká. To proto, že metoda předpokládá, že funkci lze nahradit prvním diferenciálem a ten jako lineární rovnici použít k hledání kořene:

f(x1) = f(xo+dx) = f(xo) + f'(xo) dx = 0

a tedy

x1 = xo+dx = xo - f(xo)/f'(xo)

Jako příklad použijeme snad nejjednodušší možný problém - výpočet převrácené hodnoty čísla. Představme si na chvíli, že Pascal spolu s umocňováním neovládá ani dělení. Co teď? Podíl a/b můžeme vyjádřit jako součin a s převrácenou hodnotou b. Jak ale spočíst převrácenou hodnotu? Zkusíme hledat kořen rovnice
f(x) = b-1/x
Newtonova motetoda říká,. že pokud vezmeme xo dostatečne blízko kořene bude číslo

x1 = xo+dx = xo - f(xo)/f'(xo) = x + x(1-bx)

ještě mnohem blíže. Vidíme, že na vypočtení nám stačí pouze násobení a sčítání. Že by bylo možné převést dělení na sérii násobení a sčítání?

Nejdříve to zkusíme pro konkrétní hodnotu např. 0.9 a první přiblížení převrácené hodnoty odhadneme na 1.1. K jaké posloupnosti přiblížení převrácené hodnoty 1/0.9 povede Newtonova metoda?

xo =1
x1 =1.1
x2 =1.111
x3 =1.1111111
x4 =1.111111111111111

Vidíme, že zatímco půlení intervalu by přidalo 0.3 cifry na iteraci, dosáhli jsme v každém kroku zdvojnásobení počtu platných cifer a potřech iteracích musíme skončit, protože již neumíme čísla ukládat přesněji. Chování chyby se dá studovat obeně, my ale pro jednoduchost použijeme konkrétní funkci odpovídající výpočtu převrácené hodnoty.

Metoda regula falsi

Ne vždy ale dokážeme spočítat hodnotu derivace. Jistým vylepšením metody půlení intervalu je předpokládat, že funkce mezi body a a b vypadá téměř jako úsečka a zkoušet místo půlky intervalu vzít jako kandidáta na kořen prusečík této sečny s osou x, tedy

Nyní se podobně jako u půlení intervalu rozhodneme podle znaménka f(c) tak aby kořen ležel ve zvoleném intervalu. Pro funkce, které nemění v blízkosti kořene znaménko druhé derivace tato metoda neustále upravuje jen jednu mez, jak uvidíme v našem příkladu s dělením:

[a0,b0] = [1, 1.200000000000000]
[a1,b1] = [1, 1.120000000000000]
[a2,b2] = [1, 1.112000000000000]
[a3,b3] = [1, 1.111200000000000]
[a4,b4] = [1, 1.111120000000000]
[a5,b5] = [1, 1.111112000000000]
[a6,b6] = [1, 1.111111200000000]
[a7,b7] = [1, 1.111111120000000]
[a8,b8] = [1, 1.111111112000000]
[a9,b9] = [1, 1.111111111200000]
[a10,b10] = [1, 1.111111111120000]
[a11,b11] = [1, 1.111111111112000]
[a12,b12] = [1, 1.111111111111200]
[a13,b13] = [1, 1.111111111111120]
[a14,b14] = [1, 1.111111111111112]
[a15,b15] = [1, 1.111111111111111]

Zjednodušeně se dá říci, že v každé iteraci přibude tolik cifer, na kolik se trafíme na začátku. Jakkoli nemůže tato metoda kořen "ztratit", může se stát, že se metoda regual falsi chová i hůře než půlení intervalu.

Metoda sečen

To že jeden z krajních bodů zůstával v minulé metodě trčet na místě, výrazně snižovalo rychlost konvergence. Pokud upstíme od požadavku různých znamének funkce f v bodech a a b, můžeme mít vždy po ruce poslední a předposlední aproximaci kořene a z nih počítat odhad polohy kořene podle stejného vzorce. Ten navíc upravíme na následující tvar:

Všimněte si, že jmenovatel ve složeném zlomku je aproximací derivace funkce. Protože se nyní obě hodnoty přibližují kořeni, nepřekvapí, že účinnost metody se blíží Newtově metodě.

[a0,b0] = [1.000000000000000, 1.200000000000000]
[a1,b1] = [1.200000000000000, 1.120000000000000]
[a2,b2] = [1.120000000000000, 1.110400000000000]
[a3,b3] = [1.110400000000000, 1.111116800000000]
[a4,b4] = [1.111116800000000, 1.111111114751999]
[a5,b5] = [1.111111114751999, 1.111111111111092]
[a6,b6] = [1.111111111111092, 1.111111111111111]

Cvičení: Napište programy, které vypíší postup hledání kořene, a zkotrolují, zda jsem si ta výše uvedená data nevycucal z prstu.

Neplánované chyby při běhu programu

Následujíc program nám vypíše jako výsledek číslo 0. Je to pochopitelný, ale nejspíš nechtěný jev. Chyba spočívá v tom, že číslo 256 nepatří do rozsahu typu byte, který je 0..255.

program test;
var i : byte;
begin
  i:=255;
  i:=i+1;
  writeln(i);
  readln;
end.

Proto program trochu ozdobíme:

program test;
uses SysUtils;
var i : byte;
{$RANGECHECKS ON} {kamkoli nad radek i:=i+1}
begin
  i:=255;
  i:=i+1;
  writeln(i);
  readln;
end.

Vložením {$RANGECHECKS ON} komentáře začínajícího zankem dolaru jsme překladač uplatili, aby do přeloženého kódu přidal kontrolu na meze při přiřazování a indexování polí. Pozor tedy na znak $ nacházející se za složenou závorkou nebo jejím dálnopisným ekvivalentem (*, trerý také může omezovat komentář. Po přidání {$RANGECHECKS ON} se vypsání nuly nedočkáme, místo toho se pos tsiknutí F9 (zkratka pro spuštění programu) objeví varování:

a my po odklepnutí OK musíme v menu vývojového prosředí Delphi zvolit Run/Program Reset abychom se zbavili toho modrého zvýrazněného řádku s chybou.

Pokud místo práce ve vývojovém prostředí nastane chyba při běhu aplikace spuštěné z příkazové řádky, jsme upozorněni známým varováním, že program selhal:

Pokud by mezi importovanými kniovnami nebyla knihovna SysUtils, skončil by program jen vypsáním chybové hlášky, což nám většinou nestačí pro nalezení a odstranění chyby:

C:\Projects\prog\pokusy>test
Runtime error 201 at 00402570

C:\Projects\prog\pokusy>

Podobně jako se výsledek nemusí vejít do proměnné, může se také stát, že se výsledek aritmetické oprace, řekněme násobení, vůbec nevejde do překladačem předpokládané délky slova 32 bitů, a operace vrací nesmysly. V tomto případě jde o jiný typ chyby, tzv přetečení a odpovídá jí jiný přepínač: {$OVERFLOWCHECKS ON}, v krátkém (turbopascalovém) znění {$Q+}.

program test;
uses sysutils;
var j : integer;
{$OVERFLOWCHECKS ON}
begin
  j:=50000;
  j:=j*j;
  writeln(j);
  readln;
end.

Používáme knihovny ( Velmi úvodní poznámky)

Uvedení žádosti o použití knihoven, např.

Uses SysUtils;

musí následovat před oddílem deklarací a má formu rezervovaného slova uses následovaného seznamem identifikátorů oddělených čárkami a ukončeného, ovšem, středníkem.

Import knihovny pomocí konstrukce

uses IdKnihovny1,IdKnihovny2,...,IdKnihovnyN;

si můžeme představit jako zkratku za napsání deklarací všeho co uvedené knihovny exportují. Přečteme-li si v nápovědě:

Unit
SysUtils

function IsLeapYear(Year: Word): Boolean;

Description
Call IsLeapYear to determine whether the year specified by the Year parameter is a leap year. Year specifies the calendar year.

znamená to, že v knihovnou SysUtils je kromě jiného poskytována fukce, která pro letopočty z rozsahu 0..65535 vrátí logickou hodnotu určující, zda jde o rok přestupný, či nikoli. Použijeme-li tedy spojení
uses SysUtils;
můžeme funkci IsLeapYear používat, jako bychom si její deklaraci do programu napsali sami.

Jak jsme viděli na chování běhových chyb, použití knihovny může mít své důsledky, aniž vůbec použijeme jakoukoli funkci či proceduru z knihovny. Bohužel však podrobnější popis přesahuje rámec přednášky.

Z desítek knihove stndardně dodávaných s Delphi 6, bude pro nás asi zajímavější knihovna Math, sdružující mnoho užitečných matematických funkcí opatřených rozumnými identifikátory. Jsou mezi nimi např. goniometrické funkce (ArcCos), umocňování (Power), převodní funkce (DegToRad) atp.
Pokud si pamatujeme alespoň počáteční písmena identifikátoru, můžeme využít pomoci, kterou nám nabízí pracovní prostředí:

Pokud po napsání několika písmen použijeme klávesovou zkratku Ctrl-Mezera, objeví se nám výběr identifikátorů začínajících na daná písmena. Po napsání kompletního identifikátoru a otvírací závorky nám navíc editor nabídne nápovědu v podobě seznamu formálních parametrů a jejich typů:

V knihovně Math je definováno nepřehledné množství goniometrických a příbuzných funkcí
ArcCos,ArcCosh,ArcCot,ArcCotH,ArcCsc,ArcCscH,ArcSec,ArcSecH,ArcSin,ArcSinh
ArcTan2,ArcTanh,Cosh,Cosecant,Cotan,CotH,Csc,CscH,Sec,Secant,SecH,Sinh,Tan,Tanh
a dále např.
Sign(x) ... vrací -1,0,+1 tak aby x = Sign(x)*Abs(x)
Ceil(x) ... nejmenší celé vetší
Floor(x) ... nejvetší celé menší
nebo logaritmy
Log10(x)
Log2(x)
LogN(10,x)
funkce pro umocňování
Power(10,x)
IntPower(3,k)
zaokrouhlování
RoundTo(x,-2) ... na dvě desetinná místa
porovnávání reálných čísel s tolerancí
if SameValue(x,y,1E-10) then ...
if CompareValue(x,y,1E-12)<=0 then ....

Rozhodně tu nemůžeme očekávat Besselovy funkce a pod.

I data mají svou strukturu

Kromě deklarací proměnných, konstant, procedur a funkcí můžeme v jazyce Pascal deklarovat i nový typ. Prozatím jsme používaly několik jednoduchých typů:

Integer (a příbuzné varianty byte, ..., int64)
Real (i ten má kratší variantu: single)
Boolean

Char

Dalším jednoduchým typem je char. Konstanta tohoto typu se zapisuje jako
1. jeden znak mezi apostrofy, např. ' ' (mezera) nebo '*' nebo '''', což je jediný znak apostrof.
2. znak # následovaný číslem v rozsahu 0..255. Toto číslo může být též psáno pomocí znaku $ v hexadecimálním zápisu, např. #9 (znak tabulátor), #32 (mezera) je totéž jako #$20 nebo samozřejmě ' '. Souvislost mezi číselným zápisem a příslušným znakem je dána tabulou kódů, která se z historických důvodů jmenuje ASCII (americký standardní kód pro výměnu informací).

#$20=#32= ' '  '!'  '"'  '#'  '$'  '%'  '&'  '''' '('  ')'  '*'  '+'  ','  '-'  '.'  '/'
#$30=#48= '0'  '1'  '2'  '3'  '4'  '5'  '6'  '7'  '8'  '9'  ':'  ';'  '<'  '='  '>'  '?'
#$40=#64= '@'  'A'  'B'  'C'  'D'  'E'  'F'  'G'  'H'  'I'  'J'  'K'  'L'  'M'  'N'  'O'
#$50=#80= 'P'  'Q'  'R'  'S'  'T'  'U'  'V'  'W'  'X'  'Y'  'Z'  '['  '\'  ']'  '^'  '_'
#$60=#96= '`'  'a'  'b'  'c'  'd'  'e'  'f'  'g'  'h'  'i'  'j'  'k'  'l'  'm'  'n'  'o'
#$70=#112='p'  'q'  'r'  's'  't'  'u'  'v'  'w'  'x'  'y'  'z'  '{'  '|'  '}'  '~'  #127

Znaky #0..#31 nemají původně význam znaků ale kontrolích povelů (původně pro dálnopis).
Znak #9 se nazývá tabulátor, znaky #10 a #13 mají význam přechodu na nový řádek, případně jen "návratu vozíku".
Ostatní znaky z tohoto rozsahu mohou mít podle situace význam řídícího znaku nebo jen třeba jen znaku srdíčka. Pokud k tomu nemáme dobrý důvod (např. níže zvědavost) neposíláme do textového výstupu kontrolní znaky a pro řádkování používáme Writeln. Ten vypíše na každé platformě platnou sekvenci kontrolních zanků pro přechod na nový řádek. S tabulátorem nebývají potíže.

Proměnná typu char se deklaruje podle očekávání jako

var c : char;

Pro ujasnění významu znaků mezi 9 a 13 vyzkoušejte co vypíše

writeln('abcd',#13,'12');

Případně jednoduchý cyklus

var c:char;
...
for c:=#9 to #13 do 
begin
  writeln(ord(c),':');
  writeln('abcd',c,'12');
end;

Jak vidíme, proměnná typu char může vystupovat jako řídící proměnná cyklu for.
Pořadí znaku v tabulce (tedy číslo, kterým počítač znak representuje) získáme použitím funkce ord. Naopak znak z celého čísla vyrobíme použitím konverse typu tak, že idnetifikátor typu použijeme jako funci s jedním parametrem. Proto následující kód dá stejný výstup.

var i:integer;
...
for i:=9 to 13 do 
begin
  writeln(i,':');
  writeln('abcd',char(i),'12');
end;

Proto také můžeme místo ord(c) psát integer(c).

Spolu s celočíselnými typy je typ char příkladem tzv ordinálního typu, tedy typu repsesentujícího množinu s bobře definovaným uspořádáním, 1:1 zobrazitelnou na nějaký (konečný-víc se nám do počítače nevejde) interval celých čísel. Pro takovou množinu je pak rozumné definovat funkce předchůdce (pred) a následník (succ).

pred('B') = 'A', pred(0) = -1, succ(7) = 8 atp.

Deklarace typu

Následující řádek deklaruje typ int a to jako integer.

type int = integer;

tím získáme možost ušetřit si trochu psaní. Můžeme ale také napsat

type integer = int64

a naučit náš program počítat místo do 2 147 483 647 až do 9 223 372 036 854 775 807. Tím že takto počínaje touto deklarací zastíníme původní význam identifikátoru si ovšem můžeme přidělat řadu starostí, takže jde o trik nevhodný pro seriózní práci.

Je zřejmé, že takto bychom se daleko nedostali, pouze bychom mohli nazývat star=é věci novým jménem. Pascal přináší řadu dalších způsobů, jak zkonstruovat nový typ.

Typ Interval

Nejjednodušší možností je prohlásit, že proměnná smí nabývat pouze hodnot z jistého intervalu ordinálního typu:

type tCisloPoslance = 1..200;
     tMalePismeno   = 'a'..'z';
     tRocnikZS      = 1..9;

var  PredsedaPK : tCisloPoslance;
     Vychodil   : tRocnikZS;

Takto máme možnost přenechat komilátoru starost o to, aby nám nehlasovalo příliš mnoho poslanců nebo zda vyplnili správně svoji povinnou školní docházku. Prostřednictvím chybových hlášení při kompilaci či běhu se tak můžeme dozvědět o nesrovnalostech.

Uvidíme později, že daleko nejdůležitějším užitím typu interval je určení mezí polí, které chápe Pascal jako zobrazení z intervalu do množiny dané typem prvku pole.

Výčtový typ

Je jakýmsi zobecněním typu interval, kde si můžeme prvky sami pojemnovat a nejde jen o podmnožinu výchozího typu.

type Fukce = (Radovy, ClenVyboru, PredsedaKlubu);

deklaruje nejen nový typ ale též nové hodnoty v podobě identifikátorů. Kormě funkce ord, která nám dává
ord(Radovy) = 0, atd... máme opět k disposici také succ a pred, takze plati
succ(Radovy) = pred(PredsedaKlubu)
Pro počítač je tahle deklarace podobná svým významem následující

const Radovy = 0;
      ClenVyboru = 1;
      PredsedaKlubu = 2;
type  Funkce = Radovy..PresedaKlubu;

ovšem jde o izolovaný ty a nemůžeme do proměnné výčtového typu přiřadit celé číslo. To zvyšuje bepečí při psaní programu.

Pozor identifikátory prvků výčtového typu nám moho něco zastínit, nebo vést ke kolizi, takže i zde musíme dávat pozor při volbě jmen. Situace je velmi podobná té při deklaraci const ClenVyboru = 1;

Někdy má smysl "Maďarská notace":

type tFukce = (eRadovy, eClenVyboru, ePredsedaKlubu);

Zde je jiný příklad:

type tKarty = (
    ZelenaSedma,  ZaludovaSedma,    KulovaSedma,    SrdcovaSedma,
     ZelenaOsma,   ZaludovaOsma,     KulovaOsma,     SrdcovaOsma,
  ZelenaDevitka, ZaludovaDevitka,  KulovaDevitka, SrdcovaDevitka,
  ZelenaDesitka, ZaludovaDesitka,  KulovaDesitka, SrdcovaDesitka,
   ZelenySpodek, ZaludovySpodek,   KulovySpodek,   SrdcovySpodek,
   ZelenySvrsek, ZaludovySvrsek,   KulovySvrsek,   SrdcovySvrsek,
     ZelenyKral,   ZaludovyKral,     KulovyKral,     SrdcovyKral,
      ZeleneEso,    ZaludoveEso,      KuloveEso,      SrdcoveEso
              );

type tSedmy = ZelenaSedma..SrdcovaSedma;
     tOsmy  = ZelenaOsma..SrdcovaOsma;
     {...}

var  SedmaKDalsimuPouziti : tSedmy;
     LibovolnaKarta    : tKarty;

begin
  LibovolnaKarta := ZaludovyKral;
  SedmaKDalsimuPouziti := SrdcovaOsma; //[Error] pokus.dpr(28): Constant expression violates subrange bounds
...
  LibovolnaKarta := ZaludovyKral;
  SedmaKDalsimuPouziti := LibovolnaKarta;

  writeln( ord(SedmaKDalsimuPouziti)); // Writeln neumi vypsat vyraz vyctoveho typu 
  readln;
end.

Množiny

Z výše uvedených typů můžeme budovat typ množina:

program test;
type tCharSet = set of char;

var  PouzitaPismena,RozbiteKlavesy : tCharSet;
     c : char;
begin
  RozbiteKlavesy := ['x','q','X','Q'];
  PouzitaPismena := []; //prázdná množina

  repeat
    read(c);
    PouzitaPismena := PouzitaPismena+[c];
  until c='.';

  if PouzitaPismena*RozbiteKlavesy = [] then Writeln('Mohu Pouzit Tento Psaci Stroj')
          else Writeln('Musim Pouzit Jiny Psaci Stroj');

  readln;
  readln;
end.

Konstruktor množiny: má podobu hodnot a intervalů oddělených čárkami v hranatých závorkách.
K disposici jsou obvyklé množinové operace:

Sjednocení +, průnik *, rozdíl -. Logické operace nad množinami jsou jen podmnožina <=, nadmnožina >= , rovnost = a různost <>. Klíčové slovo in lze použít ke konstrukci dotazu na přítomnost prvku v množině, takže

LogProm := Znak in Mnozina;

je totéž jako

LogProm := [Znak] <= Mnozina;

Dálnopisným ekvivalentem znaku [ kombinace (. a podoně .) nahradí znak ] .

Z výše definovaného typu tKarty můžeme sestavit množiny

const sSedmy = [ZelenaSedma..SrdcovaSedma];
      sOsmy  = [ZelenaOsma..SrdcovaOsma];
           {...}
      sEsa   = [ZeleneEso..SrdcoveEso];

a testovat hodnotu karty vyrazem (k in sSedmy) misto (k<=SrdcovaSedma) and (k>=ZelenaSedma).

Alignment a packed record (array)

V současných počítačích je vyzvednutí hodnoty proměnné z paměti, které musí předcházet libovolné operaci s proměnnou, velmi náročnou operací, např. ve srovnání s časem potřebným pro sečtení dvou celých čísel. Aby se urychlila práce počítače, vyzvedává více bytů najednou, řekněme že 8. Pro optimální běh programu je pak vhodné, aby procesor dokázal načíst např. celé číslo (4 byty) na jedinou operaci přístupu do paměti. Nejjednodušším řešením tohoto problému je, že každá položka záznamu o velikosti 4 byty začíná na adrese dělitelné 4 a podobně pro proměnné velikosti 8 bytů. To znamená, že se v pamě»ovém prostoru pro uložení záznamu nacházejí nevyužitá místa. Konkrétní způsob uložení je nejlépe vyzkoumat experimentálně, protože je dán použitým překladačem. Někdy může být plýtvání opravdu velké:

type rec_brb = record
       a:byte; //tady nasleduji 7 práznych bytů
       j:real;
       b:byte; //tady nasleduji 7 práznych bytů
     end;

     rec_bb = record
       a:byte; 
       b:byte; 
     end;

...

Writeln( sizeof(rec_brb) );  //   --> 24
Writeln( sizeof(rec_bb) );   //   --> 2

Tedy pro uložení 10 bytů informace, použil překladač 24 bytů pamě»ového prostoru. To jsme zjistili použitím universální funkce sizeof, která jako parametr akceptuje identifikátor typu nebo proměnnou libovolného typu (jde jakoby o předávání odkazem, takže ne libovolný výraz) . Vrátí pak počet bytů, který proměnná či typ zabírá.

Zabránit takovémuto zarovnávání (angl.: alignment) můžeme použitím klíčového slova packed v deklaraci typu.

type rec_brb = packed record
       a:byte; 
       j:real;
       b:byte;
     end;

Tentokrát bychom dostali velikost záznamu 10 byte.

I naskládání položek v poli může být ze stejných důvodů plýtvavé. Proto i před slovem array se může nacházet slovo packed, pokud chceme zařídit aby se šetřilo místem.

Strukturované typy II - Pole

(anglicky array) je již od počátku počítačového věku nejdůležitější datovou strukturou.

Píšeme

const Dim = 3;
type  tVektor3 = array[1..Dim] of real;
var a : tVektor3;
    x : real;
    i : integer;
    b : tVektor3;

a myslíme tím, že proměnná a je skupina tří reálných čísel. Při deklaraci strukturovaného typu pole musíme uvést typ prvku pole a typ indexu. Typ indexu musí být ordinální typ s dostatečně malým rozsahem hodnot. Většinou píšeme místo typu indexu rovnou interval, ale nikdo nám nebrání psát

type  t3Dindex = 1..Dim;
      tVektor3 = array[t3Dindex] of real;

Operace s Poli: Přístup k prvku pole

S jednotlivými prvky pole můžeme pracovat zvláš» tak, že za identifikátor proměnné typu pole přidáme v hranatých závorkách index:

a[1] := 0; 
a[2] := x+1; 
a[3] := x-1;

Identifikátor pole následovaný výrazem v závorkách je první příklad toho, kdy designator není pouhý identifikátor. Vzpomeneme-li si na synatktické diagramy z druhé přednášky, uvidíme, že přístup k prvku pole můžeme použít na levé straně přiřazovacího příkazu stejně jako ve výraze, pokud tam můžeme použít proměnnou typu z něhož je pole utvořeno.

x := a[1]+a[2]+a[3];

je tedy správně zapsaný přiřazovací příkaz. Kdybychom jako indexy používali pouze konstanty, vystačili bychom se třemi proměnnými a1, a2, a3. Důležité je, že jako index můžeme použít libovolný výraz kompatibilní s typem indexu udaným při deklaraci. Výše uvedený součet tedy můžeme zapsat cyklem.

x := 0;
for i := 1 to Dim do x := x + a[i];

Podobně jako v přiřazovacím příkazu může me použít prvek pole jako parametr.

for i := 1 to Dim do Writeln(i, ' ' , a[i]);

Vzhledem k deklaraci spadá ve všech krocích i do intervalu 1..Dim a nedojde tedy běhové chybě. Již víme, že při deklaraci pole musíme uvést typ prvku pole a typ indexu. Při přístupu k prvku pole, a» již na některé ze stran přiřazovacího příkazu, nebo jako parametru volání procedury či funkce, teď kromě samozřejmé podmínky na typ prvku pole (ani nyní nemůžeme psát CelePole[i]:=RealnePole[i] ), musíme navíc dbát o to aby index byl v povolených mezích.

Operace s Poli: Přiřazení

Pokud vytvoříme nový typ, neumí Pascal s proměnnými tohoto typu příliš zacházet. Kromě setupu na nižší úroveň, což pro strukturovaný typ pole je použití konstrukce Ident[index], umí jazyk Pascal přiřazovat mezi dvěma proměnnými stejného typu. Dva typy s odlišnými identifikátory jsou stejné pokud jsou navzájem svázány řadou rovnítek v deklaraci typů, kde na obou stranách rovnítka je jen a pouze identifikátor.

type  Typ1 = array [1..6] of integer; 
  Typ2 = array [1..6] of integer; 
  Typ3 = Typ1;
  Typ4 = Typ1; // Typ3 je stjený s Typ2

var     Z1,Y1: Typ1;
  Z2,Y2: Typ2;
  Z3   : Typ3;
  Z4   : Typ4;

...
   Z1 := Y1;  // OK
   Z3 := Z1;  // OK
   Z2 := Y2;  // OK
   Z3 := Z4;  // OK
...
   Z1 := Z2;  // NE!
   Z2 := Z3;  // NE!

Chceme-li rozšířit schopnosti jazyka pracovat s nově definovaným typem, musíme použít procedury a funkce, které mají některý z parametrů tohoto typu.

Operace s Poli: Procedury a funkce

Z předchozího vyplývá, že naše vektory nemůžeme sčítat, jak bychom chtěli:

type tVektor3 = array[1..3] of real;
var a,b,c : tVektor3;
    x    : real;
...
   a := b+c; // NE!!!!

Bohužel, Pascal nám ( až na výjmimy jako je překladač FreePascal ) neumožňuje dodat definici operace '+' pro pole. Proto musíme psát:

procedure SectiV3( a,b : tVektor3; var c : tVektor3);
begin
   c[1] := a[1]+b[1];   
   c[2] := a[2]+b[2];   
   c[3] := a[3]+b[3];
end;
...
   SectiV3(b,c, a);

nebo

function SectiV3( a,b : tVektor3) : tVektor3;
begin
   SectiV3[1] := a[1]+b[1];   
   SectiV3[2] := a[2]+b[2];   
   SectiV3[3] := a[3]+b[3];
end;
...
   a := SectiV3(b,c);

Tato druhá varianta vypadá přehledněji, ale jde spíše o výjimečné použití funkce vracející hodnotu strukturovaného typu. Jde o konstrukci, kterou připouštějí až současné překladače Pascalu. Měli bychom mít na paměti, že v tomto případě probíhá stěhování výsledku nadvakrát, nicméně, možnost zapsat formulky aspoň trochu čitelně je příjemná:

 a := SectiV3(VektorovySoucin(b,c),VektorovySoucin(d,a));

Kdy předávat pole odkazem?

Až na výjimky pokaždé! Proto náš příklad

   a := SectiV3(b,c);

s vektorovou algebrou byl špatně hned dvakrát. nejen, že zbytečně kopíroval jeden výsledek funkce do cílové proměnné při přiřazení, ale především dvakrát kopíroval hodnotu obou parametrů předávaných hodnotou. Proto pro seriózní práci s poli budeme muset všechna předání pole uskutečnit odkazem. Tím přijdeme o možnost psát Součetpoli(VektorovysSoucin(a,b),c). Protože pole mohou být opravdu velká a mohou zabírat velké množství paměti, může být dalším důvodem i neúnosná spotřeba paměti. Obecně musíme dbát o to aby režie při volání procedury a navracení výsledku nebyla příliš velká (kolik je únosné? 5 nebo 50% ?).

Konstantní parametry

Přesto existuje možnost, jak nekopírovat hodnoty hodnotou předávaných parametrů, kromě předání parametrů odkazem a hodnotou máme totiž (v posledních letech) k dispozici tzv. konstantní parametry.

function SectiV3(const a,b : tVektor3) : tVektor3;
begin
 SectiV3[1] := a[1]+b[1]; 
 SectiV3[2] := a[2]+b[2]; 
 SectiV3[3] := a[3]+b[3];
end;

Tím překladači sdělíme, že hodnotu parametru nehodláme měnit, a on s ním bude zacházet šikovněji, především si nebude vytvářet kopii. Jak víme, hlavička procedury nebo funkce obsahuje nejn informaci pro kompilátor, ale vyjadřuje i záměry autora. Identifkátor funkce by měl říkat co vrací. Identifkátor procedury, co dělá, a idnetifikátory parametrů by měly být také výmluvné. Pokud je naším záměrem, aby konkrétní parametr sloužil pro vstup hodnoty, je vhodné jej označit jako konstantní. Tím se vyvarujeme možné vchyby, kdy se prostřednictvím parametru předávaného hodnotou pokusíme něco vrátit. Kompilátor si bude stěžovat. Vyzkoušejte!

Pole s více indexy

Z typu tVektor3 bychom mohli deklarací

type tMatice3 = array [1..Dim] of tVektor3;

vyrobit typ tMatice3. Poté bychom mohli psát

var M: tMatice3;
    b: tVektor3;

....

M[1][1]:=1; M[1,2]:=0; M[1,3]:=0; ....

b := M[1];

Naproti tomu deklarace

type tMatice3 = array [1..3] of array [1..3] of real;

nebo její zkrácená podoba

type tMatice3 = array [1..3,1..3] of real;

by nám nedovolila přiřazovat vektory do M[1] atd.

Příklady použití polí

Pole mají pro nás nepřeberné množství užití. Pro představu pár příkladů:

Seznam (index je jen pořadím v seznamu a nemá sám o sobě význam)

var TazenaCisla : array [1..6] of 1..49;

Časové řady (index je stále pořadím, ale má význam, lze z něj spočíst kdy došlo k odečtní hodnoty)

var Teplota : array [1..PocetVzorku] of real;

2D data

var Teplota : array [1..PocetVzorkuX,1..PocetVzorkuY] of real;

2D obrázek (zatím stupně šedi)

type tPixMap = array [1..PocetPixluX,1..PocetPixluY] of byte;
var PixMap : tPixMap;

3D data

var Teplota : array [1..PocetVzorkuX,1..PocetVzorkuY,1..PocetVzorkuZ] of real;

Tabulka funkčních hodnot

var Faktorial : array [0..170] of real; // 171! se do proměnné typu real nevejde
    Binomial  : array [0..1000,0..1000] of real; //zkuste urcit presnejsi meze !!!

Tabulka na překódovani

var TajnyKod : array[char] of char;    
 ObrazkyKaret: array[tKarta] of tPixMap; 
          s1 : array[integer] of char; //[Error] pokus.dpr(25): Data type too large: exceeds 2 GB
          s2 : array[real] of char;    //[Error] pokus.dpr(26): Ordinal type required

Poslední dva řádky nejsou správně a je u nich uvedena chyba, kterou nám překladač ohlásí.

Paměťové nároky polí

Pole mohou velmi snadno vyčerpat dostupnou pamě». U polí s jedním indexem to ještě není příliš aktuální. Pokud budeme ale psát program por odšumování audionahrávek a celou nahrávku se pokusíme nacpat do paměti najednou, můžeme narazit i tady. Pro představu si připomeňme známý fakt, že hodina stereofonní nahrávky v CD kvalitě nám zabere přes půl gigabytu (vzorek tvoří 2x16 bitů, rychlost vzorkování je 44 100 za sekundu). Daleko snazší je vyčerpat pamě» při práci s poli se dvěma indexy. Takový RGB obrázek v rozlišení 10 000x10 000 zabere 300MB. Reálná matice se stejnými rozměry zabere skoro gigabyte. Jestliže se nám může číslo 10 000 velké a můžeme doufat, že tak velké matice potřebovat nebudeme, ve třech dimenzích se situace ještě zhorší. Budeme-li chtít nějakou fyzikání veličinu definovanou v prostoru studovat na počítači, často nám nezbyde, než si prostor redukovat na prostorovou mříž a pracovat s hodotami v uzlech této mříže.

program KrychloHydro;

const N = 200;

type tGridFunction = array [1..N,1..N,1..N]

var p,vx,vy,vz : tGridFunction;

....

Výše uvedený začátek programu pro naivní počítačovou hydrodynamiku na krychli předpokládá, že na krychli o hraně dvěstě bodů budeme definovat tři komponety rychlosti a tlak. Těmito několika řádky jsme si vyžádali 256 MB paměti. Podle povahy problému se ukáže, jestli nám 200 bodů stačí. Pokud budme potřebovat více, nesmíme zapomenout, že spotřeba paměti roste se třetí mocninou N.

Než budete psát diplomovou práci, pravděpodobně vzroste typická kapacita pamětí osobních počítačů 10x. To ovšem znamená, že dovolené N vzroste pouze dvakrát.

Eratosthenovo síto

je další klasický algoritmus, a navíc ilustruje, že pole potřebovali již antičtí informatici.

program Sito;

const N = 50000000;

var MaDelitel : array[0..N] of boolean;
i,p : integer;

begin
  p:=2; //prvni prvocislo

  repeat
    {krok 1: oznacim vsechny nasobky prvocisla p}
    i:=p+p;
    while i<=N do begin
      MaDelitel[i]:=true;
      i:=i+p;
    end;

    {krok 2: najdu dalsi prvocislo}
    p:=p+1;
    while MaDelitel[p] {tedy neni to prvocislo} do p:=p+1;

  until p*p>N; // a to cele opakuji....

//ted spoctu pocet prvocilel od 2 do N
  p:=0;
  for i :=2 to N do if not MaDelitel[i] then p:=p+1;
  Writeln('Existuje ',p,' prvocilsel <= ',N);
  Readln;
end.

Důležitá poznámka: Pro přehlednost využívá algoritmus triku a to, že se spoléhá na vynulování globálních proměnných. (Je to oprávněný předpoklad, ale pokud bychom z hlavního programu učinili proceduru, přestane fungovat! Museli bychom přidat vynulování pole MaDelitel[]. ) Po skončení hlavní smyčky repeat-until můžeme hodnoty v poli nějak využít. V příkladu se spočte, kolik prvočísel je od 2 do N.

Můžeme ale hodnoty vypsat, uložit do souboru a následně si i vykreslit obrázek. Zde je například nakresleno relativní zastoupení prvočísel v intervalu 2..N:

Obrázek byl vykreslen následující řadou povelů pro program gnuplot:

gnuplot> set data style lines
gnuplot> set logscale x
gnuplot> plot 'SeznamPrvocilsel.Dat' using 1:($0+1)/($1-1)

$1 zde znamená hodnotu čísla v prvním sloupečku (soubor obsahuje jen jeden sloupeček) a $0 je pořadové číslo hodnoty (ta první má samozřejmě pořadové číslo 0).Všimněte si, že v intervalu 2..3 je 100% prvočísel.

Typ záznam

Struktorovaný typ se skládá z menších kousků, podobně jako strukturovaný příkaz se skládá z "menších" příkazů, jednoduchých i strukturovaných (for for if). V případě pole byly jednotlivé kousky stejného typu a přístup k nim jsme měli pomocí indexace. V Pascalu máme ale ještě jednu možnost.

type tVectorXYZ = record
                    x,y,z : real;
      end;
var  a,x  : tVectorXYZ;

begin
  a.x := 1;
  a.y := -1;
  a.z := 0;

  x   := a;
  x.x := 2;

...

end.

Podobně jako u polí můžeme

Přistupovat k menším kouskům, z nichž je strukturovaný typ složen pomocí konstrukce IdentProm.IdentSlozky
Přiřazovat celou proměnnou do jiné stejného typu
Předávat proměnnou (nebo výsledek volání funkce) jako parametr (tři způsoby)

Je libo pole záznamů nebo záznam s poli?

Samozřejmě můžeme kombinovat podle uvážení obě konstrukce a designátory nabyvaji na kráse:

type tComplex = record
                 Re,Im : real
    end;
     tCV3     = array [1..3] of tComplex;
     tRGB     = packed record 
       R,G,B : byte;
          end;

     tKomlexniPuntik 
             = record  
                  x     : tCV3;
      barva : tRGB;
               end;

var  A : tKomlexniPuntik ;
     b : tRGB;

...

A.x[2].Im := 0;
A.x[1].Re := -1;

...

Inicializované proměnné a konstanty.

Dokud jsme pracovali jen s jednoduchými proměnnými, nebyl problém na začátku programu napsat pár přiřazení a inicializovat obsah proměnných. Pole nebo záznmay ale mohou být delší a jejich inicializace sérií přiřazovacích příkazů by byla nepohodlná. Mohou nastat dva případy

A) hodnoty je třeba inicializovat před výpočtem a ty se již nemění.
B) hodnoty je třeba inicializovat před výpočtem, a ty se poté budou dále měnit.

K tomu můžeme použít následující konstrukce se syntaxí:

DeklaraceIniKonstProm: (var | const) Ident : Typ = IniKonstVyraz ';'
IniKonstVyraz: KonstVyraz | '(' SeznamIniKonstVyrazu ')'
SeznamIniKonstVyrazu: IniKonstVyraz (',' IniKonstVyraz)*

a zde jsou příklady s inicializovanými poli :

const iFaktorial : array [0..12] of integer = (1,1,2,6,24,120,720,5040,40320,
                 362880,3628800,39916800,479001600);
var   ObjemNadob[1..PocetNadob] = (0,0,10);
      CisloKroku : integer = 0;

Konstrukce výrazu typu pole je dovolen jen v deklaraci inicializované proměnné nebo typované konstanty, do přiřazovacího příkazu nemůžeme použít

  ObjemNadobi:=(1-x,x,y);
  ObjemNadobi:=(0,0,11);

Pozor, některé dřívější verse jazyka Pascal neumějí variantu s var a i proměnné se deklarují jako const.

type tSeznamAz10Cisel
         = record
             Pocet : 0..10;
             Cisla : array [1..10] of integer;
           end;

var Dlouhy : tSeznamAz10Cisel = (Pocet : 8; Cisla : (1,2,3,4,5,6,7,8,0,0) );
    Kratky : tSeznamAz10Cisel = (Pocet : 2; Cisla : (1,2,0,0,0,0,0,0,0,0) );

Samozřejmě můžeme inicializovat i jednoduché proměnné.

var   Oddelovac : char = ',';
      CisloKroku : integer = 0;

Proměnné z vícenásobná deklarace jako třeba

var   a,b : char ;

nemohou být inicilizovány. Neinicializované globální proměnné jsou při startu programu inicializovány na 0 (a to i tehdy, když 0 nepatří do jejich intervalu atp.), zatímco lokální proměnné obsahují před prvním použitím smetí. Typované konstanty smí být lokální (tedy deklarovány v bloku nějaké procedury či funkce), inicializované proměnné nikoli a jsou bohužel dovoleny jen na globální úrovni.

Variantní záznam

Někdy chceme ukládat jednotlivé položky přes sebe. To proto, že význam má jen jedna z nich a rezervovat místo na ty ostatní je zbytečné. Předpokládejme, že si chceme udělat pořádek v plechových geometrických součástkách na našem skladu. Taková plechová součástka je popsaná materiálem, tlouš»kou plechu, tvarem a rozměry. Rozměry trojúhelníku se ale určují pomocí tří čísel zatímco u kruhu stačí jen poloměr.

program CaseTest;

type
   tTvar = (tvObdelnik, tvTrojuhelnik, tvKruh);
   tMaterial = (mtHlinik,mtOcel);
   tPlechovyUtvar = record
                     Material:tMaterial;
                     Tloustka:Real;
                     case Druh:tTvar of
                       tvObdelnik: (Vyska, Sirka: Real);
                       tvTrojuhelnik: (StranaA, StranaB, StranaC: Real);
                       tvKruh: (Polomer: Real);
                     end;

function Obvod(W:tPlechovyUtvar):real;
begin
  if W.Druh=tvObdelnik    then Obvod:=2*(W.Vyska+W.Sirka);
  if W.Druh=tvTrojuhelnik then Obvod:=W.StranaA+W.StranaB+W.StranaC;
  if W.Druh=tvKruh        then Obvod:=W.Polomer*2*Pi;
end;

Cvičení: dodělejte funkce pro plochu, objem a hmotnost součástek.

Endiáni: (J. Swift)

Cvičení: Pomocí variantního záznamu prozkoumejte proměnnou typu integer jako pole 4 bytů. Je zřejmé, že pokud do celého čísla typu integer uložíte hodnotu 1, pak ve třech bytech bude 0 a v jednom 1, o tom říkáme, že je nejméně výnamný. Zjistěte jestli váš počítač ukládá nejméně významý byte na nejnižší nebo naopak nejvyšší adrese. (Předpokládmáme ovšem, že pole se ukládá vždy tak, že s rostoucím index roste i adresa uložení.)

Strukturované příkazy With a Case

Příkaz With

Účel příkazu with vysvětlí nejlépe příklad.

type tComplex = record
                 Re,Im : real
    end;
var  z : tComplex;
     Re: Real;

...

Re := 1;
with z do 
begin
  Re := 0;
  Im := 1;
end;
Writeln (Re,' ',x.Re);

Vypíše ' 1.00000000000000E+0000 0.00000000000000E+0000', protože unvitř příkazu with přestala být vnější proměnná Re vidět a byla zakryta identifikátorem složky záznamu z.

Příkaz Case

je příkaz, který jsem doposud tajil. Občas se ale hodí nahradit řadu podmíněných příkazů např.

if n=0 then f:=1
else if n=1 then f:=x
else if n=2 then f:=x*x
else if n=3 then f:=x*x*x
else if n=4 then begin f:=x*x; f:= f*f; end;
else begin
  f:=exp(ln(x)*n);
end;

následujícím strukturovaným přikazem

case n of
 0:  f:=1;
 1:  f:=x;
 2:  f:=x*x;
 3:  f:=x*x*x;
 4:  begin f:=x*x; f:= f*f; end;
 else 
  f:=exp(ln(x)*n);
end;

Část začínající else lze vynechat a také můžeme místo jednoho čísla psát seznam čísel a intervalů, které se ale nesmějí překrývat

case c of
 '-':           n:=-n;
 'a'..'z','_':  n:=n+1;
 'A'..'Z', 
 '0'..'9','$':  n:=n-1;
end; // kód nemá žádný význam

Pole s volným koncem - zarážka

V mnoha případech neznáme v okamžiku kdy píšeme program, kolik hodnot bude v poli potřeba uskladnit. Běžným řešením je odhadnout shora maximální rozumný počet a pole dimenzovat na tuto maximální zátěž. Jde o velmi běžný postup a i některé solidní programy (TeX) vám někdy nahlásí, že jste vyčerpal kapacitu a musíte si program překompilovat s větší konstantou určující kapacitu polí pro uskladnění.

Jak ale do takovéhoto pole naskládat seznam s proměnnou délkou. Prvním řešením je použití zarážky. Jde o to, že za posledním uloženým prvkem nastavíme ten další na nějakou dohodnutou hodnotu, jež nás upozorní, že již nejde o data ale o oznámení konce. V kódu pak procházíme pole dokud nenarazíme na zarážku. Pokud je procházení pole součástí zamýšleného kódu, nepřidá kontrola na zarážku příliš práce a není ani příliš náročnější než si pamatovat rovnou počet údajů v poli. Technologie zarážky se běžně používá u jednoho typů polí: řetězců. Zatímco Pascal s implementací řetězců nejdříve otálel, jiný jazyk jeho éry, C, který musel od počátku sloužil pro psaní skutečných programů, rozhodl, že dnes je nejčastějším způsobem uložení řetězců takzvaný zero-terminated string. Nejčastějším proto, že dnešní OS mají kdesi na počátku právě operční systém, kvůli jehož psaní si K&R vymysleli jazyk C. Proto až budeme potřebovat komunikovat na nižší úrovni s OS, budeme se muset spokojit s touto nejjednodušší formou řetězce. V následujícím příkladu požádáme OS ( = Windows, konkrétně) aby nám sputili (angl. execute) program ping. Ten bez paramtrů vypíše nápovědu a skončí. Proceduře zajiš»ující komunikaci s OS, WinExec, musíme předat parametr právě jako nulovou zarážkou ukončené pole znaků. Proceduru WinExec nalezneme exportovanou v knihovně (UNIT) Windows, která exportuje 4373 funkcí, 92 procedur a 180typů, které můžete použít ke komunikai s aplikační vrstvou OS a jeho nadstaveb (tím se má říci, že když blufujeme o počítačích, hodí se rozlišovat v pro nás monolitním "OS" vlastní OS, nadstavby, vnitřnosti,...).

program pokus;

uses Windows;

var cmd : array[0..1234] of Char;
      i : integer;

begin
   cmd := 'ping'; // Nějaký "příkaz" reprezentovaný exe-souborem, nikoli copy či dir
   WinExec(cmd,1);// Řekni OS aby příkaz vykonal
   Sleep(1000);   // Za 1000 ms by to už mohlo být hotovo, WinExec totiž nečeká

   i := 0;        // Příklad velmi jednoduché práce znak po znaku
   while cmd[i]>#0 do begin
     writeln(cmd[i]);
     i:=i+1;
   end;

   readln;
end.

V cyklu while je vidět jednoduchý příklad na operaci s každým znakem nulou ukončeného řetězce. Příkaz
cmd:='ping'
ukazuje další z výjimek v kompatibilitě typů. Stručně je shrneme na konci přednášky. Zde jen, že by se to nepřeložilo, kdyby byl typ pole např. array[1..1234] of Char, tedy tyto nejen nulovým znakem ukončené (vlastnost uložení dat) ale i nulovým indexem počínající jsou (důležitá formalita).
Pozor, zarážka je jen jedna. Když ji přehlédnete, mohou za ní následovat bežné znaky a na další zarážku už v poli vůbec nemusíte narazit, index tak překročí hranice pole a mohou se začít dít věci.

Cvičení: Napište vnitřnosti následujících procedur:

type tStrZ = array[0..1024] of Char;

procedure SpojRetezce(const A,B: tStrZ; var AaZaNimB: tStrZ);

function DelkaRetezce(const A: tStrZ) : integer;

procedure KusRetezce(const A: tStrZ; OdKterehoZnaku,KolikZnaku: integer; var VybranuKusA: tStrZ);

Pole s volným koncem - proměnná pro délku

Je zřejmé, že místo abychom na určení délky řetězce měli zvláštní funkci, která jen počítá počet znaků před zarážkou, můžeme přidat ještě proměnnou, která bude vždy říkat, kolik hodnot máme v poli uloženo.
Typické použití je v následujícím kódu: Když už umíme ukládat řadu hodnot do pole, můžeme si ukázat jak tato data načteme z klávesnice.

{$RANGECHECKS ON} 
const Max = 1000;
var PocetHodnot : integer = 0; //inicializovaná proměnná
    Hodnoty     : array[1..Max] of real;
    x : real;

begin
 Writeln('Zadejte až ',Max,'kladných reálných čísel');
 Writeln('Zadávání ukončete záporným číslem nebo nulou.');
 
 ReadLn(x);  
 while x>0 do begin
   PocetHodnot :=  PocetHodnot + 1;
   Hodnoty[PocetHodnot] := x;
   ReadLn(x);  
 end;
 
 Writeln('Načetl jsem ', PocetHodnot, ' čísel. Příště s nimi i něco udělám');

end.

Takto obvykle vypadají programy z učebnic zpracovávající vstup dat . Jde o to načíst řadu čísel, něco s ní udělat (v našem případě jsme je jen naskládali do pole), přičemž konec vstupu je indikován nějakým číslem mimo rozsah povolených hodnot. Jakkoli jsme tedy odstranili zarážku z našeho popisu dat uvnitř programu, zůstala tu stále zarážka jako konečník vstupních dat.

Poprvé je zde použita funkce ReadLn k něčemu lepšímu než jen k čekání na stisk klávesy Enter. Jde o vylepšenou versi proceury Read, která umí načíst ze vstupu (nebo souboru, to uvidíme později) data několika základních typů: Celé číslo, reálné číslo, jeden znak a řetězec znaků (uvidíme dále). ReadLn pak ještě přečte a zahodí všechny znaky do konce řádku včetně. Naproti tomu Read pokračuje tam, co skončila.

Pole s volným koncem - proměnná pro délku a pole sbalené do záznamu

Proměnné Hodnoty a PocetHodnot jsou úzce svázány a zvláště ta první bez druhé není použitelná. Mohlo by nás napadnout spojit je do jednoho záznamu a chápat je jako jednu (strukturovanou) proměnnou.

type tHodnoty  = record 
          Pocet : integer;
          Data  : array[1..Max] of real;
     end;

Víme, že Pascal s nově definovaným typem příliš zacházet neumí, nezbude nám, než si pro něj napsat sadu procedur a funkcí a nebo jednoduše psát Hodnoty.Data[Hodnoty.Pocet]. V situaci, kdy náš program musí zacházet s několika různě dlouhými seznamy dat může spojení k sobě příslušných dat a metadat do jedné struktury zvýšit pohodlí a bezpečí.

Pole s otevřeným koncem (dynamická pole)

Námi používaná verse Pascalu nám umožňuje ještě lepší řešení:


program DynArrTest;

var Hodnoty : array of real;
    x : real;
    kam : integer;
begin
 Writeln('Zadejte libovolný počet kladných reálných čísel');
 Writeln('Zadávání ukončete záporným číslem nebo nulou.');
 
 ReadLn(x);  
 while x>0 do begin
   Kam:=High(hodnoty)+1; //Low(Hodnoty) je 0
   SetLength(Hodnoty,Kam+1);
   Hodnoty[Kam] := x;
   ReadLn(x);
 end;

 Writeln('Načetl jsem ', High(hodnoty)+1, ' čísel. Tady jsou jejich druhe mocniny:');

 for kam := 0 to High(hodnoty) do
   Writeln(Hodnoty[Kam],sqr(Hodnoty[Kam]));

 readln;
end.

Od předešlého se program hlavně liší tím, že pole Hodnoty má jako spodní mez intervalu indexů nulu. Počet prvků pole můžeme měnit procedurou SetLength(Pole,JakDlouhe). Aktuální horní mez zjistíme pomocí funkce High. Dolní mez si můžeme zjistit s pomocí funkce Low, ale bude to vždy nula a nelze ji měnit. Funkce Low a High můžeme použít i pro běžná pole, ale tam nám vrátí konstantu danou příslušnou mezí intervalu indexu, a může to být třeba i znak, když je má příslušné pole typ indexu char.

První položka pole s volným koncem má index nula.
Na počátku je High(Pole) = -1, takže ani ta není k dispozici
Po provedení SetLength(Pole,N) je poslední prvek pole Pole[N-1]
Protože SetLength musí najít dostatčně velký kus volné paměti na souvislé uložení pole, může se při změně délky provádět kopírování starých hodnot na nové místo.
Nové prvky vzniklé po SetLength mají obecně nedefinované hodnoty, výjimkou jsou pole řetězců.
Původní místo zůstává nevyužito až dokud se pro něj nenajde použití při nějaké další operaci SetLength

Následující program má být varováním, že při volání funkce SetLength mohou přestat platit odkazy na původní prvky pole.

program PozorNaNe;

type tCA = array of Char;
var A,B : tCA ;


Procedure UdelejDveVeci(var X : tCA; var c:char; N : integer);
begin
   SetLength(X,N);
   X[0]:='A';
   c:='X';  // tady je ten prusvih, c uz nemusi odkazovat na spravne misto.
end;

begin
   SetLength(A,10);
   SetLength(B,10);

   UdelejDveVeci(A,A[0],10); 
   Writeln(A[0]);            
  
   UdelejDveVeci(A,A[0],100); // Nejspis staci 13
   Writeln(A[0]);             // Uz to pise 'A'

   readln;
end.

Pokud bychom kromě SetLength(X,N) měnili ještě velikost jiných polí, mohlo by se stát, že paramtr c nebude odkazovat do prázdna jako nyní, ale přiřazení c:='X' naruší některé z těchto polí, které po změně velikosti skočilo na pamě»ovém místě původního pole A.

Pole s otevřeným koncem jako formální parametr

pokud deklarujeme formální parametr typu array of real tak jako v následujícím příkladu, můžeme při volání předat jako hodnotu

libovolné pole reálných čísel
dynamické pole reálných čísel
pole zkonstruované přímo na místě aktuálního parametru a zapsané jako [Vyraz,Vyraz,...,Vyraz]

program test;

type tDP = array of real;
var    b : array[char] of real;
       c : tDP;

function Soucet(const V:array of real) :real;
var i : integer;
    s : real;
begin
  s:=0;
  for i := low(V) to high(V) do s:=s+V[i];
  Soucet:=s;
end;

begin
  Writeln(Soucet(b));       // vypíše 0 nebo» statické pole je inicializováno na 0
  Writeln(Soucet(c));       // vypíše 0 nebo» dynamické pole nemá na počátku ani jeden prvek
  Writeln(Soucet([0,1,2])); // vypíše 3
  Readln;
end.

Je třeba roszlišit jeden malý rozdíl mezi předchozími dvěma příklady. V prvním byl parametr typu tCA a šlo tak o dynamické pole. Pro něj je definována operace SetLength. Naproti tomu v druhém případě byl typ formálního parametru array of... . Z minula víme, že formální parametr typu array [interval] of NejakyTyp, není povolen, protože by nebyl komaptibilní s žádnou proměnnou a proceduru by nebylo možno vůbec použít. Formální parametr typu array of je tedy moderní konstrukcí určenou k tomu aby bylo možno funkci předat pole s nějakým základním typem ale libovolnými mezemi. S dynamickými poli se shoduje v tom, že Low vrací vždy 0, i když definiční interval byl třeba 1..3 nebo 'a'..'z'. High je tak rovno (délka_pole - 1).

Řetězce

Zatím jsme používali řetězce jen na komentování výsledků v příkazech Writeln. Řetězce, tedy pole znaků, mohou ale sloužit k lecčemu a některé z úloh formulovaných zcela přirozeně pro řetězce jsou, nahlíženo okem informatiků, docela složité. Jako rekreaci doporučuji si prohlédnout třeba nějakou literaturu k hledání nejdelšího společného podřetězce dvou řetězců, úlohu, která může být docela užtečná třeba u analýzy DNA. Právě pro rozsáhlost problému budeme řetězce studovat jen velmi utilitárně a vyhneme se mnoha detailům a problémům.

Řetězcové konstanty

Již víme vše o znacích a řetězce jsou speciální pole znaků. Protože by bylo nepříjemné psát něco jako
('A','h','o','j',' ','l','i','d','i','!')
lze v Pascalu zapisovat řetězcové konstanty takto 'Ahoj lidi!'.

Writeln('''Apostrof uvnitr retezce  ('') se pise jako dva ('''')''');

Vypíše: 'Apostrof uvnitr retezce (') se pise jako dva ('')'

Typ String

Naneštěstí přes všechnu snahu o pravidelnost v Pacsalu se ukázalo, že užitečné věci jsou nepravidelné. Příkladem jsou třeba řetězce. Jde o složitý problém. Již jsme viděli, že kvůli spolupráci s OS mají speciální význam pole znaků se spodní mezí intervalu indexů 0. Z historických důvodů je jazyce Object Pascal připraveno několik variant řetězcových typů. Povíme jen něco málo o typu string.

var s,t : string;
    i,j : integer;

begin
  s := 'ABCD1234'; {Přiřazení konstanty do řetězce}
  t := s;            {Přiřazení hodnoty  s do t}
  Writeln(t);        {Vypíše 'ABCD1234'}

  t := copy(s,2,3);  {Přiřazení výsledku funkce do proměnné, kus počínaje druhým dlouhý tři}
  t[1] := 'B';
  Writeln(t);        {Vypíše 'BCD'}

  Delete(s,1,4);     {Vypustí 'ABCD'}
  Writeln(s);        {Vypíše '1234'}

  t := '..'+s;     {Složení řetězce z kousků}
  Writeln(t);        {Vypíše '..1234'}

  Insert('xx',t,2);
  Writeln(t);        {Vypíše '.xx.1234'}

  Writeln('Retezec '''+t+''' ma delku ',Length(t)); {délka řetězce ve znacích}
  Writeln('Podretezec ''23'' se nachazi na indexu ',
           Pos('23',t),  {nalezení polohy podřetězce jinak 0}
           ' retezce '+t);

  Setlength(t,20);
  t[20]:='6';
  Writeln(t);        {Vypíše '.xx.1234           6' ale ty mezery nejsou mezery, jak uvidíme:}
  for i:=1 to length(t) do
         Write('#',ord(t[i]));
                     {Vypíše '#46#120#120#46#49#50#51#52#0#0#0#0#0#0#0#0#0#0#0#54'); }

  str(Pi:20:10,s);  {Nacpi Pi do retezce}
  Writeln(#10#10#10#10+s); {čtyři novéřádky a Pi}
  val(copy(s,11,10),i,j);  {převeď řetězec na číslo}
  Writeln(i);     {Vypíše 1415926536}
  Readln;
end.

Ještě máme po ruce další spoustu procedur a funkcí např. UpperCase

Velmi důležitá je někdy funkce

procedure Val(S; var V; var Code: Integer)

která umí do celočíselné nebo reálné proměnné V dosadit hodnotu zapsanou v řetězci. Code je 0 pokud nenastanou problémy, jinak je to index problematického znaku v řetězci.
Interně je typ string podobný poli znaků s otevřeným koncem, první znak řetězce (pokud má délku >0) se ale nachází na indexu 1. Proto SetLength(Retezec,Delka) znamena výjimečně, že použití Retezec[Delka] je OK.

Proceduru SetLength(Retezec,Delka) použijeme především tehdy, pokud chceme pomocí indexů pracovat s jednotlivými znaky řetězce (buď vědomě za jeho aktuální délkou, nebo ji jednoduše nezáme). V rámci přiřazovacího příkazu a při volání systémových funkcí pracujících s řetězci tuto funkci folat smozřejmě nemusíme.

Ve výjimečných případech se může hodit vědět, že řetězec s neproměnnou délkou se deklaruje jako

type tJmenaReckychPismen = string [10]; //zadne neni delsi

Jde ale o přežitek z minulosti, třeba jen tím, že v hranatých závorkách smíme uvést jen číslo do 255.

Typ Text

Wirthův Pascal odrážel ještě nerozvinutý obor skladování dat té doby. Pro praktické použití souborového systému, který nám OS nabízí, můžeme samozřejmě použít přímé volání služeb OS. Pro představu tady je zjednodušená hlavička knihovnou Windows exportované funkce pro zápis dat:

function WriteFile(hFile: integer; // uchopitko (cislo) souboru
                   const Buffer;   // data
       nNumberOfBytesToWrite: integer; // kolik zapsat
                   var lpNumberOfBytesWritten: integer): boolean;

Nad podobnými funkcemi, které v podstatě nabízejí jen různé formy stěhování binárních dat mezi soubory a proměnnými, máme již od ranných verzí jazyka TurboPascal k dispozici také prostředky pro práci s datovými a textovými soubory na úrovni jazyka Pascal. Stále ale když pracujeme se souborem, musíme respektovat, že je to objekt spadající do kompetence OS a v jazyce máme jen vrátka, skrze která nám je dovoleno provádět se soubory užitečné operace pohodlněji, mnohá omezení však zůstávají.

Nejdříve budeme uvažovat vstup z a výstup do textového souboru. Dnes již je jakýkoli textový soubor posloupností bytů, nikoli štítků či bloků na pásce nebo magnetickém bubnu. Textový soubor je soubor, ve kterém, co byte to znak nebo řídící znak. (Pozn. byte ve smyslu nejmenšího kvanta zapsatelného do souboru, 8 bitů, nikoli jako předdefinovaný typ ObjectPascalu pro krátké neoznaménkované číslo.) Poslední dobou ani to již není tak prosté háčky, čárky a hyeroglyfy všech národů se spojily v Unicode a tak příští generace studentů programování bude muset překousnout 16-bitové znaky! Pokud neplatí jednoduchá rovnost co byte (word) to znak, mluvíme souboru binárním. Příkladem může být třeba soubor nějakého obrázku: Nehomogenní skládačka z binární hlavičky souboru následované bloky, každý se svojí hlavičkou a komprimovanými daty .... Práci s takovým souborem si necháme na jindy.

V Pascalu je textový soubor (tedy klíč od oněch ony dveří do světa) zastoupen proměnnou typu Text. Takto vytvoříme (nebo pokud existuje zkrátíme na nulovou délku) textový soubor s názvem 'Soubor.txt' v běžném adreáři a zapíšeme do něj krátkou zprávu:

var T: Text;
begin
 Assign(T,'Soubor.txt');
 Rewrite(T);
 Writeln(T,'Toto je prni radek souboru, druhy zustane prazdny!');
 Close(T);
end.

Co se souborem můžeme dělat nám velmi určuje OS, on je za něj zodpovědný. Proto i proměnné representující soubory zdědí jistá omezení. Především, je zakázáno přiřazení do proměnné typu Text. Navíc nemá pro nás přístupnou vnitřní strukturu, takže nemůžeme psát něco jako T.Name := 'Soubor.txt'. Zbývá tak jen třetí způsob práce s proměnnou typu Text, a to použití této proměnné jako parametr procedury nebo funkce. I zde jsme omezeni, nesmíme předávat soubor hodnotou. Proto všechny oprace se soubory budou mít formu volání procedur, kde jako první parametr bude proměnná typu Text. Následujícími procedurami, které podobně jako třeba ReadLn umí překladač aniž se musíme doprošovat nějaké knihovny, můžeme ovládat práci s textovými soubory.

Assign(TextVar, Retezec) ... Přiřazení jména. Musíme zadat platné jméno na daném stroji.
Rewrite(TextVar) ... Vytvoř soubor nulové délky a otevři pro zápis. Pokud existuje zahoď co je v něm.
Append(TextVar) ... Otevři soubor pro zápis na jeho konci. Připisuje se za původní obsah. Musí existovat.
Reset(TextVar) ... Otevři soubor pro čtení. Musí před tím existovat.
Close(TextVar) ... Uzavři soubor.

Mezi voláním Rewrite a Close (případně Append a Close) můžeme psát do soubor pomocí příkazů Write a Writeln, viz výše uvedený příklad. Mezi voláním Reset a Close můžeme ze souboru číst pomocí Read a ReadLn.

Pokud se vyskytne problém dostaneme buď
Runtime error 2 at 0040432E
nebo o něco hezčí okénko s oznámením, že se nám počítač a tvůrci programu omlouvají....

Jak víme chování se dá v případě chyby ovlivňovat pomocí direktiv. Jako obvykle, máme na výběr mezi krátkou a dlouhou formou:
Samo od sebe (default) je hlídání nastveno na {$I+} t.j. {$IOCHECKS ON} a dostaneme výše uvedené chování.
V případě, že je hlídání "vypneme" {$I-} t.j. {$IOCHECKS OFF}, pozastaví se vykonávání operací vstupu a výstupu až do doby, než se na zeptáme funkce

function IOResult : integer; // je k dispozici vždy, nepotřebujeme žádnou knihovnu

Ta nám vrátí 0, pokud nenastaly problémy. Pokud vrátí něco jiného, znamená to že nastaly problémy a podle hodnoty se můžeme dohadovat, co se stalo. Především jsou ale od okažiku volání IOResult opět povoleny operace se soubory.

Pokud tedy chceme např. vědět, zda nějaký soubor existuje, můžeme výše uvedeného chování využít a psát

function SouborExistuje(const Jmeno) : boolean;
var T:text;
begin
   {$IOCHECKS OFF}
   Assign(T,Jmeno);
   Reset(T); // pokud není, vznikne chyba a pozastaví se další operace
   Close(T); // nesmíme zapomenout, kdyby existoval
   SouborExistuje := IOResult=0;
   {$IOCHECKS ON}
end;

Jak tušíme, důvody proč nám OS nedovolí ze souboru číst můžou být různé a výše uvedená funkce opravdu jen testuje jestli je operace Reset pro daný soubor povolena. Pokud potřebujeme detilnější informace o souboru, nezbyde než se zeptat OS přímo.

Příkazy Write a WriteLn

Obecně se vyskytují ve dvou variantách:

Write(PromTypuSoubor, Vyraz, ...)

nebo

Write(Polozka, ...)

V prvním případě je první parametr proměnná typu Text a výstup probíhá do příslušného souboru, jeho obsah je tentýž jaký v druhém případě skončí na standardním výstupu (konsoli, přesměrovaný někam...).

Jak vidíme Write a Writeln nejsou obyčejné procedury a nemají ani obyčejné parametry. Především jich mohou mít libovoný počet výrazů mnoha typů (celočíselné, reálné, řetězce, znaky, logické). Dále za výrazem mohou následovat i dva další celočíselné výrazy oddělené od toho prvního dvojtečkami, které určují formát výstupu, tedy způsob, jímž se hodnota převede to textové podoby. Za první dvojtečkou se nachází šířka pole, do níž je třeba hodnotu vypsat. Pro reálné výrazy může za druhou dvojtečkou následovat počet desetinných míst.

Vyzkoušejte jak se chovají následující příkazy textového výstupu.

  Writeln(Pi);
  Writeln(Pi:5);
  Writeln(Pi:10);
  Writeln(Pi:15);
  Writeln(Pi:20);
  Writeln(Pi:25);

  Writeln(Pi);
  Writeln(Pi:30);
  Writeln(Pi:30:0);
  Writeln(Pi:30:4);
  Writeln(Pi:30:8);
  Writeln(Pi:30:12);
  Writeln(Pi:30:16);
  Writeln(Pi:30:20);
  Writeln(Pi:30:24);

Podobně můžeme psát

  Write('':i);

a vypsat tak i-krát mezeru.

Writeln je znám dobrou vůlí vypsat výstup i když se hodnota nevejde do předepsané šířky. V tom případě se vypíše v minimální nutné šířce. Bohužel to většinou příliš nepomůže:

 for i := 995 to 1005 do Writeln(i:4,i*i:7,i*i*i:10);

vypíše 

 995 990025 985074875
 996 992016 988047936
 997 994009 991026973
 998 996004 994011992
 999 998001 997002999
100010000001000000000
100110020011003003001
100210040041006012008
100310060091009027027
100410080161012048064
100510100251015075125

Pro další strojové zpracování jsou asi data stejně nepoužitelná i když se Write tak moc snažil.

Příkazy Read a ReadLn

Fukce slouží (opět ve dvou variantách) ke čtení ze standardního vstupu nebo z textového souboru. Ve druhém případě musí být první parametr typu text.

Protože procedura Readln vždy po načtení všech parametrů přeskočí na začátek nového řádku,
vyzkoumáme. coz následujícího vstupu skočí ve kterých proměnných dále uvedených příkladů
1 2 3 4 5
10 20 30

Budeme uažovat dva kousky kódu.

Read(a,b); // a=1 b=2 
Read(c);   // c=3 zbytek se nepoužije

ReadLn(a,b); // a=1 b=2 zbytek řídku se přeskočí
ReadLn(c);   // c=10

Naproti tomu pro vstupní data ve formě

se výsledky obou kousků kódu lišit nebudou.

Samozřejmě podobně je to s načítáním hodnot reálných proměnných, formát zatím popíšeme příklady
1
+1
-1
1.23
1E10
1E+10
1.003E-10
atp. dle libosti, ovšem

1.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000E10

si ale vyloží jako 1.0 takže všeho s mírou.

Read/Readln ale umí načíst i řetězce a například následující kód načte do pole celý textový soubor

program ReadText;

var T : array of string;

 i,s  : integer;
begin
  SetLength(T,100);

  i:=-1;
  while not eof do begin
    i:=i+1;
    if (i>High(T)) then SetLength(T,2*i);
    Readln(T[i]);
  end;
  SetLength(T,i+1);

  // ted spoctu pocet znaku, abych uz s tim nactenym souborem neco udelal
  s := 0;
  for i := 0 to High(T) do s:=s+length(T[i]);

  Writeln('Soubor obsahuje ',s,' znaku na ',High(T)+1,' radcich');
  Readln;
end.

Pokud jej spustíme a jako vstup mu přesměrujeme nějaký delší textový soubor, dozvíme se, že

C:\Projects\prog\pokusy>test<"C:\Program Files\Borland\Delphi6\Source\Rtl\Win\Windows.pas"
Soubor obsahuje 1113550 znaku na 30848 radcich

Poznámka: Pokud Předěláte SetLength(T,2*i) na SetLength(T,i+1) zjistíte, že je program pro soubor s 30000 řádky nepracuje, ale jen rachtá diskem. Jakkoli jsme zatím tomu tak neříkali, program vytváří dynamické datové struktury a my narážíme na nejvlastnější problémy dynamických datových struktur, tzv. potřebu sběru odpadků. [...Pár slov na přednášce.. Čtěnáře poznámek odkazuji na pokračování přednášky.] Tak jak je program napsán nepřesáhnou odpadky po zvětšování pole dvojnásobek velikosti užitečných dat pro uložení informací o řádcích (+100), což můžeme na naší neinformatické úrovni považovat za dostatečný úspěch.

Pro základní vstup číselných hodnot jsou použitelné přímo procedury Read/ReadLn. Pro složitěji formátovaný vstupní text je nejjednodušší si vstup načíst do řetězce, v něm nalézt polohu číselného podřetězce a ten převést na číslo pomocí funkce val. Viz velký příklad na řetězce výše. Za zmínku stojí, že narozdíl od běhové chyby nebo mechanismu oznamování chyb přes IOResult, umí val vrátit přímo index znaku, který mu zabránil v převední řetězce na číslo a ošetření případné chyby tak může být méně drsné.

Reálná funkce v tabulce

Budeme se zbývat situací, kdy z nějakého důvodu musíme mít funkci v počítači uloženou jako tabulku hodnot. Bohužel ještě pár let nebude možné psát array[real] of real a tak budeme graf funkce parametrizovat celočíselným parametrem z nějakého intervalu. To už v Pascalu jde

type tIndexTabulky = 0 .. 12;
     tPolicko = array[tIndexTabulky] of real;
const HodnotyX : tPolicko = (-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5);
      HodnotyY : tPolicko = (-1.3734008, -1.3258177, -1.2490458, -1.1071487, -0.78539816, 
                             0, 0.78539816, 1.1071487, 1.2490458, 1.3258177, 1.3734008);

Pokud bychom jedno z polí nahradili explicitní funkcí indexu, stále bychom mluvili o určení funkce pomocí tabulky.

Malujeme funkci z tabulky

Již víme, že pokud vytvoříme přesměrováním standardního výstupu (kam píše běžně Writeln) soubor se dvěma sloupečky čísel, můžeme program gnuplot požádat, aby za nás namaloval pěkné obrázky. V minulé přednášce jsme se ale naučili pracovat se soubory, řetězci a dokonce spouštět jiné programy a tak můžeme všechnu tuto práci automatizovat.

Následující modul nám pomocí dvou funkcí, které exportuje, umožní malovat grafy z puntíků a lomených i kulatých čar. Modul je záměrně co nejkratší, aby bylo jeho funkci možno vysvětlit na přednášce.

Unit GnuPlot01;

Interface

Procedure MalujPole(const x,y : array of real; const Jmeno:string; const format:string = 'notitle with lines');
Procedure ZobrazGraf(const Jmeno : String; const Rozsah: String = '');

Implementation
USES windows;
{$IOCHECKS OFF}

const GnuPlotExe = 'C:\Program Files\gnuplot\wgnupl32.exe';

Procedure MalujPole(const x,y : array of real; const Jmeno:string; const format:string = 'notitle with lines');
var T : text;
    S,PP : String;
    nxy,i,index,j,ipos : integer;
const Big = 100000;
begin
   nxy := High(X);
   assert( nxy = High(Y) );

   i:=1;
   while (i<=length(Jmeno)) and (Jmeno[i]='>') do i:=i+1;

   S  := copy(Jmeno,i,Big);
   if i<=2 then begin
             {Pripad 'Soubor' nebo '>Soubor'}
             {Nejdrive prikaz pro vykresleni}
             Assign(T,S+'.plt');
             Rewrite(T);
             Writeln(T,'plot "'+S+'.dat" index 0 '+format);
             Writeln(T,'pause -1');
             Close(T);
             {Potom otevrit soubor pro vystup dat}
             Assign(T,S+'.dat');
             Rewrite(T);

           end else begin
             {pripad '>>Soubor'}
             {nactu Predchozi Prikaz do PP}
             Assign(T,S+'.plt');
             Reset(T);
             if IOResult=0 then begin
               Readln(T,PP);
               Close(T);
             end else
               PP:='';

             Rewrite(T);
             if PP='' then
                {Ted vyrobim prikaz pro vykresleni}
                Writeln(T,'plot "'+S+'.dat" index 0 '+format)
             else begin
                {Tady vylepsim prikaz pro vykresleni}
                j:=1;index := -1;
                repeat //zjistit posledni index
                  ipos := pos(' index ',copy(PP,j,Big));
                  index := index+1;
                  j := j+ipos+7;
                until ipos=0;
                Writeln(T,PP,',"',S,'.dat" index ',index,' ',format);
             end;
             Writeln(T,'pause -1');
             Close(T);
             {Potom otevrit soubor pro vystup dat}
             Assign(T,S+'.dat');
             Append(T); if IOResult>0 then Rewrite(T); //velmi hrube....
             Writeln(T);
             Writeln(T); //Pred data pridam dva radky aby to byl dalsi blok pro gnuPlot
           end;

   for i := 0 to nxy do Writeln(T,x[i],#9,y[i]);
   Close(T);
   if IOResult<>0 then MessageBox(0, 'MalujPole: Chyba pri zapisu do souboru','Chyba',MB_OK);
end;


Procedure ZobrazGraf(const Jmeno : String; const Rozsah: String = '');
const WinExecMaxKodChyby = 31;
var     CmdStr : string;
        T : Text;

begin
   CmdStr := GnuPlotExe + ' ' + Jmeno + '.plt';

   if Rozsah<>'' then begin
     { musim prikaz
       >plot "soubor" with ...
       zmenit na
       >plot [Range] "soubor" with ...}
     Assign(T,Jmeno + '.plt');
     Reset(T);
     Readln(T,CmdStr); //Nacti puvodni prikaz pro gnuplot
     Assert(Copy(CmdStr,1,5)='plot ');
     Insert(Rozsah,CmdStr,5);{Sem ^ strcit Rozsah}
     Close(T);

     Assign(T,Jmeno + '.tmp');
     Rewrite(T);
     Writeln(T,CmdStr);
     Writeln(T,'pause -1');
     Close(T);

     CmdStr := GnuplotExe + ' ' + Jmeno + '.tmp';
   end;

   // !! Trik !!
   //  1. Delphi umeji prevest String na (ukazatel na) PoleZnakuSeZarazkou napiseme-li tam PChar
   //  2. SW_NORMAL pripadne SW_MAXIMIZE rikaji jak ma vypadat okenko grafu
   if WinExec(PChar(CmdStr),SW_NORMAL) <= WinExecMaxKodChyby
          then MessageBox(0, 'MalujPole: Nenalezen WGnuPl32.exe','Chyba',MB_OK);

end;


{ ToDo:

  - kontrola spravnosti poradi formatu
  - moznost nastavit styl car
  - etc.  chybi sposta veci jde zamerne o jednoduchy kod

}
end.

Triky použité v kódu byly probrány na přednášce a jsou v kódu komentovány.

Podrobně byla probrána i struktura modulů a to, jak vyčlenit z hotového programu recyklováníhodné kusy a jak z nich vytvořit modul rozdělením na veřejné rozhraní a privátní implementační část. Čtenáře poznámek odkazuji na [Satrapa], kapitola 20.

Význam obou funkcí nejlépe objasní Příklady použití

begin

  MalujPole(HodnotyX,HodnotyY,'Priklad');

//  MalujPole(HodnotyX,HodnotyY,'Priklad','title "Data" with points pointtype 2 pointsize 2');
//  MalujPole(HodnotyX,HodnotyY,'>>Priklad','title "Lomene cary" with lines');
//  MalujPole(HodnotyX,HodnotyY,'>>Priklad','smooth csplines title "Splajny"');

  ZobrazGraf('Priklad');

end.

Význam kontrolních slovíček with points atp. je v povídání o gnuplotu a určitě ještě dodám nějakou tabulku příkladů příkazů plot v gnuplotu, aby bylo jasné, co přesně se z gnuplotu máte učit.

Interpolace

V výše uvedeném případě je rozložení hodnot nezávislé proměnné x rovnoměrné, tzv. ekvidistantní. Velmi často se s hodnotami takto rovnoměrně poskládanými setkáme u veličin měřených v závislosti na čase (např. vzorky zvuku na CD...) Data v proměnných HonotyX a HodnotyY můžeme znázornit grafem

Jak máme ale určit funkční hodnotu mezi jednotlivými body grafu? Co třeba proložit sousedními body úsečky?

Vidíme, že výsledek není příliš dokonalý, ale přesto

Cvičení: (důležité) napište funkci, která mi pro reálné x v rozsahu -3 .. 3 vrátí takto vypočtenou hodnotu a bude mít hlavičku např.

function FzTabulky(x : real) : real;

a namalujte její graf. Pokud se ke cvičení dostanete později, nezapomeňte, že v uspořádaném poli se dá hledat velmi rychle.

Pokud se nám tato hranatá funkce nezdá dost dobrá, můžeme zkusit lepší. Víme, že N+1 body můžeme proložit právě jeden polynom N-tého stupně, takže máme hned kandidát. A kolika body budeme polynom prokládat? No přece všemi, když už je máme. Tady je výsledek:

Že nevypadá stále dost dobře? No tak zkusíme někde sehnat víc bodů a to musí pomoci

Nepomohlo...

Přes toto počáteční varování jsou polynomiální interpolace velmi užitečné, a tak si o nich povíme více.
V příkladu byla ale použit lehce zákeřná funkce arcustangens a navíc aspoň uprostřed intervalu vypadá výsledek hezky.

Především problém je lineární a tak stačí zjistit jak vypadá funkce proložená implusem a tu pak oškálujeme a sečteme přes všechny vzorky. Takto vypadá impuls v x=5:

Funkce proložená vyznačenými puntíky bude určitě úměrná polynomu
Y5(x) = (x - 1)(x - 2)(x - 3)(x - 4)(x - 6)(x - 7)(x - 8)(x - 9)(x - 10)
Pokud ji vydělíme Y5(5) máme funkci na obrázku.

Takovouto úvahou dostáváme Lagrangeův interpolační vzorec

Pokud si povšimneme jmenovatelů, tak vidíme, že pro obecné rozložení bodů xi budeme muset provést N*(N-1) násobení. Protože ale není důvod předpokládat, že N bude nabývat nějakých závratných výšek, nemluvíme zde ani tak o náročnosti výpočtu jako o faktu, že kód bude obsahovat dva cykly. Samozřejmě existují i jiná schémata pro výpočet interpolace.

Cvičení: Kromě obecné procedury pro interpolaci polynomem obecného stupně, si zkuste napsat některou z řady užitečných interpolačních funkcí jako např:

function Interp2(x, x1,x2,y1,y2 : real) : real;
function Interp3(x, x1,x2,x3,y1,y2,y3 : real) : real;

atp. které určitě někde využijeme.

Příklad:

toto je funkce pro výpočet interpolované hodnoty přímo z Lagrangova vzorečku:

function LInterp(t:real; const X,Y : array of real):real;
var i,j,n : integer;
s,f : real;
begin
  n := High(X);
  {assert( n = High(Y) ); tam dame az budeme vedet co to je}

  s := 0;
  for i := 0 to n do begin
  f:=1;
  for j := 0 to n do if i<>j then f := f*(t-X[j])/(X[i]-X[j]);
    s := s+f*Y[i];
  end;
  LInterp := s;
end;

přičemž jde o přímý přepis vzorečku, bez jakýchkoli triků.

Polynomy jako pole koeficientů

Protože teď umíme spočíst fuknční hodnotu polynomu proloženého body Xi,Yi, můžeme chápat tuto dvojici vektorů také jako zápis polynomu. Obvyklé ale polynomem rozumíme spíše pole jeho koeficientů.

Následující program ukazuje jak definujeme pro takový polynom základní operace a jak je můžeme použít ke konstrukci koeficientů interpolačního polynomu. Jde o rozdílné obou přístupy a nakonec vykreslíme jejich rozdíl. (Komentář: Spočíst nejdříve koeficienty interpolovaného polynomu a pak používat Hornerovo schéma k výpočtu hodnot interpolované funkce není nejlepší.)

Program Lagr2;
Uses GnuPlot01;

type tPolynom=array of real;
{
  Pozor formalni parametry funkci jsou typu array of real
  a nikoli tPolynom, abych mohl psat
  W := SoucinPolynomu(A,[-1,0,1]); pro W:=(x^2-1)*A
}

Function HodnotaPolynomu(const P:array of real;x:real): real;
var s : real;
    i : integer;
{Spocte funkcni hodnotu polynomu pomoci Hornerova schematu}
begin
  s := P[High(P)];
  for i := High(P)-1 downto 0 do s:=s*x+P[i];
  HodnotaPolynomu := s;
end;


Function KopiePolynomu(const P:array of real): tPolynom;
var Q : tPolynom;
    i : integer;
begin
  SetLength(Q,High(P)+1);
  for i := 0 to High(P) do Q[i]:=P[i];
  KopiePolynomu := Q;
end;

Function SoucetPolynomu(const A,B:array of real): tPolynom;
var Q : tPolynom;
    i,n : integer;
    s : real;
begin
  n:=High(A);
  if nj then f := SoucinPolynomu(f,[-X[j]/(X[i]-X[j]),1/(X[i]-X[j])]);
     s := SoucetPolynomu(s,f);
   end;
   InterpolacniPolynom := s;
end;



function LInterp(t:real; const X,Y : array of real):real;
var i,j,n : integer;
    s,f   : real;
begin
   n := High(X);
   assert( n = High(Y) );

   s := 0;
   for i := 0 to n do begin
     f:=1;
     for j := 0 to n do if i<>j then f := f*(t-X[j])/(X[i]-X[j]);
     s := s+f*Y[i];
   end;
   LInterp := s;
end;



const N = 12;
type tIndexTabulky = 0 .. N;
     tPolicko = array[tIndexTabulky] of real;
const HodnotyX : tPolicko = (-3,-2.5,-2.0,-1.5,-1.0,-0.5, 0,0.5,1.0,1.5,2.0,2.5,3.0);
var   HodnotyY : tPolicko ;

const M = 1000;
var iX,iY,iDelta : array [0..M] of real;
    var i : integer;
    var xa,xb:real;
    IP : tPolynom;
begin

  HodnotyY[6]:=1;

  MalujPole(HodnotyX,HodnotyY,'Hodnoty','title "Data" with points pointtype 2 pointsize 2');
  //MalujPole(HodnotyX,HodnotyY,'>>Hodnoty',' smooth cspline title "cspline"');

  // nyni spoctu nejdriv interpolacni polynom
  IP := InterpolacniPolynom(HodnotyX,HodnotyY);

  // potrebuji vzit nasledujici rozsah promenne x
  xa := HodnotyX[Low(HodnotyX)];
  xb := HodnotyX[High(HodnotyX)];

  // a do poli nacpu hodnoty x_i a  y_i = IP(x_i)
  for i :=0 to M do begin
     iX[i] := xa + i/M*(xb-xa);
     iY[i] := LInterp(iX[i],HodnotyX,HodnotyY);
     iDelta[i] := HodnotaPolynomu(IP,iX[i])-iY[i];
  end;

  MalujPole(iX,iY,'>>Hodnoty','title "Lagrange" with lines');
  MalujPole(iX,iDelta,'Rozdily','title "Chyba IP" with lines');

  ZobrazGraf('Hodnoty','[][-1:2]');
  ZobrazGraf('Rozdily');

  { Nasledujici prikaz nas muze presvedcit, ze problem je ve vypoctu polynomu:
   Writeln(HodnotaPolynomu(IP,-3),' ',LInterp(-3,HodnotyX,HodnotyY));
   readln;
  }
end.

Cvičení: Vyzkoušejte jaké obrázky program vykreslí. Měňte počet bodů a prokládané funkce a pozorujte co se stane.

Cvičení: V jedné z minulých přednášek jsme použili rekurentní vztah pro Legendrovy polynomy. Zkuste jej pomocí funkcí uvedených v programu použít k výpočtů koeficientů Pn(x).

Cvičení: Jak je to s přesností pro polynomy vyššího řádu. Porovnejte podobně jako ve výše uvedeném programu pro interpolace.

Matice

Doposud jsme uvažovali především pole s jedním indexem. V Pascalu, jak víme, ale můžeme psát

type tMatice3x3 = array[1..3,1..3] of real;

var A : tMatice3x3
...
A[3,1] := ...

Protože jsme si definovali nový typ, musíme pro praktické použití definovat procedury a funkce.

function Det3x3(const A:tMatice3x3) : real;
begin
Det3x3 := A[1,1]*A[2,2]*A[3,3] + A[1,2]*A[2,3]*A[3,1] + A[1,3]*A[2,1]*A[3,2] 
- A[1,1]*A[2,3]*A[3,2] - A[1,2]*A[2,1]*A[3,3] - A[1,3]*A[2,2]*A[3,1] ;
end;

Často se ale stane, že rozměry matic v programu jsou jsou různé. Dokonce se může stát, že jeden program pracuje chvíli s maticemi 3x3, za chvíli 14x14 a za další chvíli 100x100 atd. V takovém případě bychom museli mít 3 různé funkce pro determinat, tři pro sčítání matic, tři pro násobení atd.

Naštěstí můžeme matici chápat jako pole řádků a tak použít deklaraci

type tVektor = array of real;
     tMatice = array of tVektor;

Oproti přednášce z algebry nazýváme vektory řádky matice, takže pozor. To proto, že chceme aby matice z Algebry
[a11 a12 a13]
[a21 a22 a23]
[a31 a32 a33],
přešly na matice
A[0,0] A[0,1] A[0,2]
A[1,0] A[1,1] A[1,2]
A[2,0] A[2,1] A[2,2]

Pokud by se někomu chtělo, může obětovat nulté prvky polí a nulté řádky matic a mít indexy počínající jedničkou.

Pro velká N budeme matici konstruovat přímo programem, ale pro nižší hodnoty bychom mohli chtít zapsat matici takto:

A := [ [0  ,1  ,1-x],
       [1+x,y  ,1  ],
       [1  ,x  ,y  ] ];

Bohužel toto zatím Pascal neumí, ale pokud si definujeme vhodné funkce, následující zápis je v pořádku:

A := _m([_v([ 0 , 4 , 0 ]),
         _v([1-x, 0 ,1+x]),
         _v([ 0 , y , 8 ])] );

Podle nálady, může jít o přijatelnější variantu série přiřazení:

A[0,0]:=0;  A[0,1]:= 4;  A[0,2]:= 0;
A[1,0]:=1-x;A[1,1]:= 0;  A[1,2]:= 1+x;
A[2,0]:=0;  A[2,1]:= y;  A[2,2]:= 8;

ve které je ale velmi snadné poplést indexy.

Už s vektory se daly dělat věci (Cvičení: zkuste si napsat proceduru pro Gramm-Schmidtovu ortogonalizaci) a v případě matic nemáme šanci ani povrchně probrat ty nejzákladnější operace (a to ani z pohledu potřeb budoucího uživatele nějaké knihovny pro práci s maticemi).

Cvičení: Po prostudování použití matic v níže uvedeném programu pro Gauss-Jordanovu eliminaci zkuste napsat operace násobení a sčítání matic.

Řešení soustavy lineárních rovnic (Gaussova - Jordanova eliminace)

Mějme soustavu 4 rovnic pro 4 neznámé:

     9y + 6z + 4w = 3
2x + 3y + 4z      = 3
 x      - 3z + 2w = 0
 x + 4y + 4z -  w = 1

Tato soustava se běžně representuje maticí

Protože matici budme chtít upravit na diagonální tvar, kde nenulové prvky budou jen na diagonále, musíme nejdříve prohodit první dva řádky (tedy první dvě rovnice, to jistě smíme):

Nyní první řádek (tedy rovnici) vydělíme tak aby na diagonále zbyla jednička - normalizace

Nyní od druhého až čtvrtého řádku odečteme vhodný násobek prvního řádku tak aby v prvním sloupci mimo diagonálu zbyly nuly (lineární kombinace rovnic je OK):

Teď již stručně - normalizace 2. řádku (nic nemusíme prohazovat)

odečtení násobků druhého řádku

Normalizace 3.řádku

Odečtení násobků 3. řádku od ostatních

Normalizace 4. řádku

Konečně, odečtení násobků čtvrtého řádku

Připoměňme, že tato matice representuje lineární systém
x = 3/4
y = 23/2
z = -33/4
w = -51/4

Celá metoda tak postupně opakuje tři kroky: podmíněné prohození řádků, normalizaci řádku a eliminaci nediagonálních elementů daného sloupce.
Technický detail: je zvykem prohazovat řádky tak, aby se na diagolále objevil v absolutní hodnotě nejjvyšší použitelný (řádek>=sloupec) člen daného sloupce. To že nestačí jen kontola na 0 tak aby šel řádek normalizovat je zřejmé, i číslo 10^-15 by nám vadilo (vyzkoušejte). To že se vyplatí najít právě v absolutní hodnodě největší prvek je už numerická matematika.

Následuje program, ve kterém je také procedura pro GJ eliminaci. Současným výpočetm pro N pravých stran se spočte inverzní matice (taková aby M M^(-1) = JednotkovaMatice).

Program Maticni;
uses Sysutils;
{Pouzivame assert a ten v Delphi-IDE neni videt bez SysUtils}

type tVektor = array of real;
     tMatice = array of tVektor;

function _v(const a : array of real) : tVektor;
{Udela z pole realnych cisel vektor}
var b : tVektor;
    i : integer;
begin
    SetLength(b,High(a)+1);
    for i :=0 to High(a) do b[i] := a[i];
    _v:=b;
end;

function _m(const a : array of tVektor) : tMatice;
{udela z pole vektoru matici}
var b : tmatice;
    i : integer;
begin
    SetLength(b,High(a)+1);
    for i :=0 to High(a) do begin
      Assert(High(a[i])=High(A[0]),'_m: Matice musi byt obdelnikova!');
      b[i] := a[i];
    end;
    _m:=b;
end;

Procedure WriteM(const M : tMatice;W:integer=9;D:integer=5);
var r,s : integer;
begin
  for r:=0 to High(M) do begin
    for s:=0 to High(M[r]) do Write(M[r,s]:W:D);
    Writeln;
  end;
end;

Function IdentM(N:integer):tMatice;
var Q  : tMatice;
    r,s: integer;
begin
  SetLength(Q,N,N);
  for r:=0 to N-1 do
    for s:=0 to N-1 do
      if r=s then Q[r,s]:=1 else Q[r,s]:=0;
  IdentM:=Q;
end;

Function TranspM(const A:tMatice):tMatice;
var Q  : tMatice;
    N,M,r,s: integer;
begin
  N := High(A);
  M := High(A[0]);
  SetLength(Q,M+1,N+1);
  for r:=0 to M do
    for s:=0 to N do
      Q[r,s]:=A[s,r];
  TranspM:=Q;
end;


function GJElim(const A,B: tMatice): tMatice;
{Samozrejme resi A.x_i=b_i pro vice pravych stran}
{Cviceni: zkuste funkci pretizit a pridat dalsi pro jedinou pravou stranu}
var M,Z : tMatice;
    t : tVektor;
    r1,r,s,N,L,rmax : integer;
    u : real;

begin
    N := High(A);  // rozmery ctvercove matice A
    L := High(A)+High(B)+1;

    Assert(N = High(A[0]),'GJElim: Matice musi byt ctvercova!');
    Assert(N = High(B[0]),'GJElim: Vektory v B musi byt spravne dlouhe!' );

    {1. A a B spojime do jedine matice}
    SetLength(M, N+1{x},L+1);

    for r := 0 to N do {radek}
      for s := 0 to N do  {sloupec}
        M[r,s] := A[r,s];
    for r := 0 to N do
      for s := 0 to High(B) do
        M[r,s+N+1] := B[s,r];

    {2. Gauss-Jordanova eliminace}
    for r := 0 to N do begin{pro vsechny radky}
      {2.1 Najdi nejvetsi |prvek| v r-tem slopecku na radcich r..N}
      rmax := r;
      s := r;     {v r-tem sloupecku, ze}
      for r1 := r+1 to N do if abs(M[r1,s])>abs(M[rmax,s]) then rmax:=r1;
      {2.2 Prehod r-ty a rmax-ty radek}
      if r<>rmax then begin
         t := M[r];
         M[r] := M[rmax];
         M[rmax] := t;
      end;
      {2.3 Normalizuj radek r}
      u := M[r,r];
      Assert(u<>0,'GJElim: Matice neni regularni');
      for s := 0 to L do begin
         M[r,s] := M[r,s]/u;
      end;

      {2.4 odecti od ostatnich radku r-ty*A[r,s] }
      for r1:=0 to N do if r<>r1 then begin
         u := M[r1,r];
         M[r1,r]:=0;
         for s := r+1 to L do
            M[r1,s]:=M[r1,s]-u*M[r,s];
      end;
    end;

    {3. Vratit vysledek}
    SetLength(Z,High(B)+1,N+1);
    for r := 0 to N do
      for s := 0 to High(B) do
        Z[s,r]:=M[r,s+N+1];

    GJElim := Z;
end;

Function InvM(const M:tMatice):tMatice;
begin
   InvM:=TranspM(GJElim(M,IdentM(High(M)+1)))
end;

var M   : tMatice;


begin

   M := _m([_v([ 0, 4, 0]),
            _v([ 2, 0, 0]),
            _v([ 0, 8, 8])] );

   WriteM(M);
   Writeln;
   WriteM(InvM(M));

   Readln;
end.

{ A takto si můžeme vyzkoušet, zda funguje transpozice 
   WriteM(_m([_v([ 11, 12, 13]),
              _v([ 21, 22, 23])] ) );
   Writeln;
   WriteM(TranspM( _m([_v([ 11, 12, 13]),
                       _v([ 21, 22, 23])] ) ));
   Writeln;
}

Časová a pamě»ová náročnost algoritmu

Vezměme jednoduchý obrázek

tušíme, že věci se zesložití, pokud vezmeme větší počet vrcholů

co můžeme říci o chování pro velký počet vrcholů (47)?

a takto vypadá detail

Nech» počet vrcholů je N. Pak se můžeme například ptát

kolik je potřeba čar k nakreslení takového obrázku ?
kolik různých průsečíků je v takovém grafu ?

Podobně se můžeme ptát třeba

jak dlouho poběží program, který bude v takovém grafu hledat nejkratší vytnutou úsečku?

Stejně tak nás může zajímat kolik paměti bude program potřebovat.

Pro každý problém zkusíme najít charakteristické N číslo udávající jeho velikost. Ne vždy je to možné ale pro představu pár příkladů:

Počet položek na skladu v programu pro skladové hospodářství.
Počet neznámých v soustavě lineárních rovnic.
Počet jednání které má vyřídit obchodní cestující.
Počet souborů, které chceme efektivně vypálit na cédéčka.

Nyní se můžeme ptát jak se bude program zabývající se výše uvedenými problémy chovat při růstu onoho charakteristického čísla N. Samozřejmě, pokud neplánujeme růst skladu, zvyšování počtu neznámých atp., nemusíme se tím zabývat. I ve fyzice se ale projevuje tendence počítat složitější a složitější problémy (třeba ty jednodušší už někdo vyřešil) a tak na problém velkého N můžeme narazit.

Při porovnávání různých algoritmů máme možnost porovnat, jak se chovají pro různé velikosti vstupních dat přímo

Někdy závisí doba řešení problému na konkrétních vstupních hodnotách, často ale, jak jsme viděli, u soustav lineárních rovnic, závisí pouze na velikosti problému.

Vzpomeneme-li si na definici algoritmu, víme že jde o posloupnost elementárních operací. Předpokládejme nejdříve, že elementárními operacemi rozumíme základní operce jako jsou sčítání, násobení, větvení, přístup k jednoduché proměnné, přístup k prvku pole volání či návrat z podprogramu atp. Změříme-li dobu, kterou potřebuje počítač k provedení každé z těchto operací a budeme-li předpokládat, že celý program se vykoná za dobu odpovídající součtu těchto jednotlivých operací, víme jak spočíst dobu potřebnou k provedení programu. Řekněme třeba, že podprogram pro skalární součin dvou vektorů

Function SkalSoucin(const A,B:tVektor):real;
var i:integer;
begin
  s:=0;
  for i:=0 to High(A) do s:=s+A[i]*B[i];
  SkalSoucin := 0;
end;

provede následující operace (časy jsou z dobrých důvodů jen přibližné a konkrétní hodnoty nedůležité, mysleme si ale, že časy jsou v nanosekundách nebo, ještě lépe, v tiknutích hodin procesoru počítače).

Operace	Čas	Počet	Celkem
Předávání parametrů	4	1	4
Vynulování proměnné	2	1	2
Zjištení horní meze pole A	30	1	30
Příprava cyklu	6	1	6
Načetní A[i]	3	N	3N
Přinásobení B[i]	6	N	6N
Přičtení s	6	N	6N
Uložení do s	4	N	4N
Zvětšení i	2	N	2N
Skok na začátek cyklu	6	N-1	6N-6
Přiřazení do výsledku	4	1	4
Návrat z funkce	10	1	10

a tedy celkový čas T = 27 N + 50.

Podobně bychom pro násobení matice vektorem dostali třeba

T = 36 N^2 + 44 N +26

Pokud nás ale zajímá chování pro větší N, je rozhodující první člen. Píšeme

T ~ 36 N^2

Určit koeficient přesně je ale velmi obtížné a asi jedinou možností je až analýza měření závislosti času výpočtu na N. Pokud chceme mluvit o výkonu algoritmu v okamžiku jeho návrhu ještě před jeho kódováním a nákupem počítače, ukazuje se, že nejjednoduuší je prostě psát

T = O(N^2)

Velké O(f) je označení pro libovolnou takovou funkci g, která splňuje vztah

0 < lim | g / f | < nekonečno pro N jdoucí do nekonečna

Následující tabulka má ilustrovat, že opravdu rozhodující je právě řád, nikoli konkrétní hodnota koeficientu u vedoucího členu.

N	N.log2 N	N^2	N^3	2^N	N!
3	6	9	27	8	6
10	30	100	1 000	1 024	3 628 800
30	150	900	27 000	1.1 E9	2.65 E32
100	700	10 000	1 000 000	1.27 E30	9.33 E157
1 000	10 000	1 000 000	1 E9	1.1 E 300	4.02 E2567
10 000	140 000	100 000 000	1 E15	2.0 E3010	2.84 E35659

Mimochodem, od velkého třesku uplynulo asi 3x10^26 nanosekund.

Vztah O(f) . O(g) = O(f . g) nám pak umožňuje místo rozkladu algoritmu na elementární kroky O(1), uvažovat strukturovaně.

Třeba Gauss-Jordanova eliminace (za předpokladu, že počet pravých stran je <=O(N) ) pro každý řádek ( tedy O(N) krát) provádí
# hledání největšího prvku na/pod diagonálou O(N)
# normalizace O(N)
# odečtení násobku řádku od všech ostatních O(N^2)

A na začátku a na konci ještě nějaké kopírování O(N^2)

Odsud máme
O(N^2) + O(N)*( O(N)+ O(N)+ O(N^2)) = O(N^3)

V tabulce si pak snadno najdeme, pro jaká N jde o zelený, oranžový či hnědý problém.

Podobně jako se s rostoucím N nějak chová čas potřebný k provedení výpočtu, nějak rostou i pamě»ové nároky. Protože nad velikostí datových struktur máme trochu lepší kontrolu, lze v praxi velmi dobře odhadnout co se vejde a co ne. V rozvahách o schůdnosti různých algoritmů ale také často vystačíme s notací velkého O.

Seznamy a jiné lineární datové struktury

Mimo jiné si zde ukážeme, že má smysl mluvit o typickém a nejhorším možném případě a jeho časové náročnosti.

Netříděný seznam

Jmeno='Pavel'
Teplota=36.5

Jmeno='Martin'
Teplota=37.5

Jmeno='Jan'
Teplota=36.9

Jmeno='Hugo'
Teplota=39.5

Jmeno='Igorl'
Teplota=37.2

Jmeno='Ivo'
Teplota=37.1

Přístup přes index.....	O(1)
Přidání položky	O(1)
Ubrání položky	O(N)
Nalezení položky	O(N)

Seřazený seznam

Jmeno='Hugo'
Teplota=39.5

Jmeno='Igorl'
Teplota=37.2

Jmeno='Ivo'
Teplota=37.1

Jmeno='Jan'
Teplota=36.9

Jmeno='Martin'
Teplota=37.5

Jmeno='Pavel'
Teplota=36.5

Přístup přes index	O(1)
Přidání položky	O(N)
Ubrání položky	O(N)
Nalezení položky podle klíče....	O(log(N))
Nalezení položky obecně	O(N)

Komentář: Nejlepší, nejhorší a typický případ pro operaci přidání.
Cvičení: napište proceduru, která v seřazeném seznamu hledá pomocí půlení intervalu a ukažte, že časová náročnost je O(log(N)).

Poznámka: toto je důležitý návod jak hledat v tabulkách funkčních hodnot pokud nejsou hodnoty nezávislé proměnné rovnou ekvidistantní, kdy se dostáváme na O(1).

Asociativní pole

Jde o velmi zajímavou a důležitou datovou strukturu. Základní idea po uživatelské stránce je mít možnost jako index použít místo pořadí rovnou klíč, třeba řetězec.

Bohužel není možné psát přímo

TeplotaPacienta := Pacineti['Pavel'].Teplota

a) protože to Object Pascal neumí b) protože není jasné jestli tam položka s klíčem 'Pavel' vůbec je

proto se přístup (vlastně vyhledání) podle klíče rodělí na dva kroky

1. Nalezení indexu k položce a ověření její existence
2. Vlasní přístup přes index

Trik spočívá v tom, že první operaci lze uskutečnit v čase O(1).

1. Nejprve se spočte hodnota tzv. matlací (hash) funkce, která přiřadí klíči celé číslo. Tato funkce musí mít velmi divokou závislost své hodnoty na klíči, rozhodně nestačí součet hodnot znaků řetězce nebo něco jiného jendoduchého, ale zároveň nesmí být výpočetně příliš náročná.
hash('Pavel') --> 1249765812

2. Poté se spočte, kde by podle matlací hodnoty měla v poli ležet hledaná hodnota
1249765812 mod VelikostPole ---> 7

3. Na indexu 7 se buď

a) nenachází nic
b) je tam hledaný prvek
c) je tam nějaký jiný prvek se stejnou hodnotou MatlaFce mod VelikostPole.
Pak se dějí věci, např. se prohlížejí všechny položky až do první prázdné, jestli není tam, když už bylo správné místo obsazené.

Důležité je, že pokud Matlafunkce funguje správně, je nepravděpopdobné, že se v jednom políčku sejdou dvě položky a bude třeba řešit kolizi, pokud máme pole dimenzováno, řekněme, třeba na dvojnásobek požadované kapacity.

Podobně se přidává prvek, hned poté, co zjistíme jestli tam náhodou už není a nejde tedy jen o přepsání.

(Pozn. Hotovou máme v Delphi bohužel jen strukturu (objekt) THashedStringList)

Více o asociativních polích se do přednášky nevejde, je ale důležité vědět, že informatici tuto strukturu promysleli a v případě potřeby máme k dipozici seznam následujících parametrů:

Přístup přes index	O(1)
Přidání položky	O(1)
Ubrání položky	O(1)
Nalezení položky podle klíče....	O(1)
Nalezení položky obecně	O(N)

Pro fyzika nabízí tato struktura možnost "kešovat" výsledky volání funkce.

Pokud výpočet funkce několika diskrétních parametrů trvá dlouho, může se vyplatit schovat si již jednou vypočtené hodnoty. Narozdíl od funkce s jedním parametrem jako je faktoriál, kde si hodnoty schováme do pole a je to, musíme v tomto případě sáhnout po složitějším řešení. Parametry dohromady tvoří klíč. Ten zamatláme a podle matlacího indexu výsledek spolu s klíčem uložíme v poli. Pokud pak potřebujeme znovu již jednou spočtený výsledek, můžeme okamžitě zjistit, zda je ještě k dispozici, nebo byla kolonka "keše" přepsána. Obvykle totiž kolize řešíme zahozením původního obsahu. To jsme u seznamu nemohli. Pokud víme, že se stejné parametry opakují 10x na každých 10 000 volání, víme, že hotovostní pamě» na 1000 výsledků nás vytrhne i když výsledky v okamžiku kolize v keši zahazujeme.

Vnitřní třídění seznamu

Třídění = řazení.Vnitřní proto, že se odehrává uvnitř polovodičové části počítače a ne třeba na magnetické pásce.

Potřebujeme mít definovanou funkci <= dvou parametrů typu položky pole k setřídění. Část položky, která obsahuje informaci potřebnou pro porovnání se nazývá klíč. Obvykle z klíče nevyplývá přímo poloha v setříděném seznamu a má význam jen při porovnání s jiným klíčem.

Seznam považujeme za setříděný, platí-li
A1 <= A2 <= A3 <= ... <= AN

Uvažujme tři příklady algoritmů pro třídění seznamu.

Třídění výběrem největšího prvku

Nejdříve najdeme mezi položkami 1..N tu největší a tu pak přehodíme s tou poslední.
Poté mezi položkami 1..N-1 najdeme tu největší a tu dáme na N-1 místo.
Atd. Algoritmus je viditelně O(N^2).

Třídění probubláváním

Spočívá v likvidaci všech míst, kde nejsou výše uvedené nerovnosti splněny. Seznam procházíme zdola nahoru a kdykoli narazíme na pár sousedních prvků seznamu, který nesplňuje pořadované řazení, oba prvky prohodíme. Když na žádnou inverzi nenarazíme, je hotovo. Jde o složitější variantu předchozího, pravděpodobně inspirovanou magnetickými páskami a jinými sekvenčními zařízeními pro ukládání dat. Počet přehazování totiž oproti minulé variantě výrazně stoupl, ale porovnávání i přehazovanání se odehrává blízko sebe.

Quicksort

je název algoritmu (Hoare cca 1960), který dokáže seřadit seznam v čase O(N log N). Využívá toho, že do přesné polohy položky mají nejvíce co mluvit ty sousední. Proto:

Rozdělí celý seznam na dvě skupiny: tu, kde jsou položky menší než nějaká zvolená a tu druhou, rozdělení probíhá přehazováním položek, které do příslušných částí nepatří.
Poté obě části předá sám sobě k rekurentnímu přeřazení. Pokud nám minulý krok rozdělí pole na zhruba dvě stejně velké části, dostáváme, podobně jako metody u půlení intervalu, jen logaritmický počet kroků, kterých je zapotřebí, abychom došli k seznamu délky 1, který již není třeba třídit.

Potíž spočívá v tom, že položku, podle které rozdělujeme seznam na dvě části, vezmeme aniž víme jestli je blízko "prostředku". Proto se může stát, že pro nevhodně uspořádaný vstup vezmeme vždy tu nejmenší/největší a skočíme u časové náročnosti O(N^2).

Cvičení: Vyzkoušejte si to napsat pro jednoduché pole čísel a) pomocí rekurze b) pomocí zásobníku.

Motivace: Otevřete si stránku http://www.cs.ubc.ca/spider/harrison/Java/sorting-demo.html s prohlédněte si animace a porovnejte rychlost výše uvedených algoritmů.Ty tam najdete pod názvy Selection Sort, Bubble Sort a Quick Sort.

Kód programu testujícího quicksort by mohl vypadat takto:

Program Sort;

procedure Quicksort(var A: array of real; l, r: Integer);
var  i, j : Integer;
     swp, rozhod: real;
begin
  rozhod := A[(l + r) div 2];

  i := l; j := r;
  while i<j do begin
    while (A[i] < rozhod)  do i:=i+1;
    while (rozhod < A[j])  do j:=j-1;
    if i <= j then begin
      swp := A[i]; A[i] := A[j]; A[j] := swp;
      i:=i+1; j:=j-1;
    end;
  end;
  if l < j then Quicksort(A, l, j);
  if i < r then Quicksort(A, i, r);
end;

var data : array [0..220000 ] of real;

       i : integer;
begin
  for i :=0 to High(data) do data[i]:=random;
  Quicksort(data,0,High(data));
  for i :=1 to High(data) do if data[i-1]>data[i] then writeln('NESETRIDEN0');
  Writeln('OK');
  readln;
end.

Potíž se tříděním dnes nespočívá v neznalosti algoritmu, ale v tom, jak naučit knihovní funkci, která třídění za nás obstará třídit data jejichž strukturu sama nezná. O tom ale příště.