#include <chrono>
#include <iostream>
#include "arrays.h"
#include "complex.h"
#include "matrix.h"
#include "misc.h"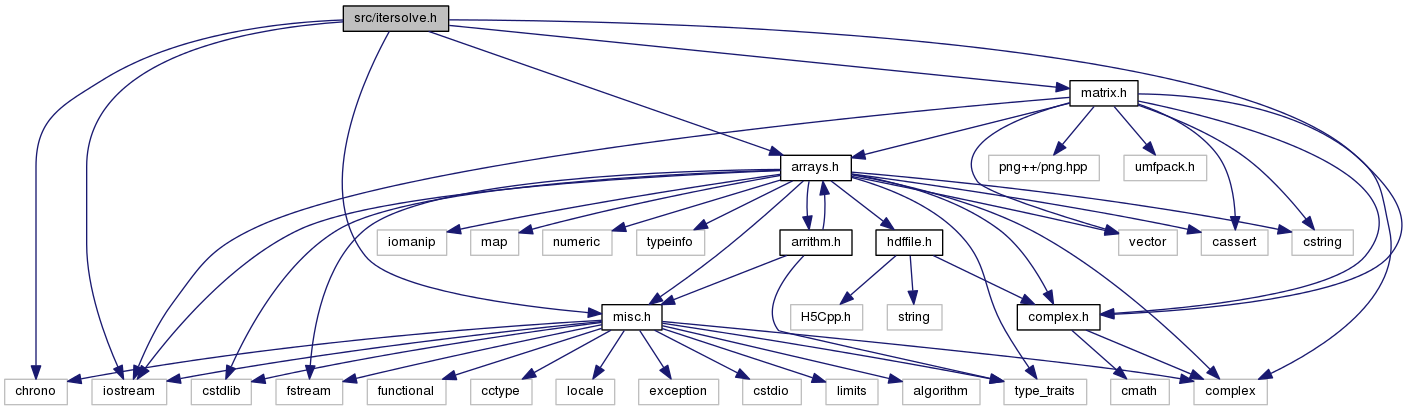

Include dependency graph for itersolve.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
cArray	default_new_complex_array (size_t n)
	Return new complex array. More...

double	default_compute_norm (const cArrayView x)
	Compute norm of an array. More...

void	default_complex_axby (Complex a, cArrayView x, Complex b, const cArrayView y)
	Do the \( \alpha x + \beta y \) operation. More...

template<class TArray , class TArrayView , class Preconditioner , class MatrixMultiplication , class NewArray = decltype(default_new_complex_array), class AxbyOperation = decltype(default_complex_axby), class ScalarProduct = decltype(operator\|<Complex>), class ComputeNorm = decltype(default_compute_norm)>
unsigned	cg_callbacks (const TArrayView b, TArrayView x, double eps, unsigned min_iterations, unsigned max_iterations, Preconditioner apply_preconditioner, MatrixMultiplication matrix_multiply, bool verbose=true, NewArray new_array=default_new_complex_array, AxbyOperation axby=default_complex_axby, ScalarProduct scalar_product=operator\|< Complex >, ComputeNorm compute_norm=default_compute_norm)
	Conjugate gradients solver. More...

template<typename TFunctor1 , typename TFunctor2 >
int	bicgstab_callbacks (const cArrayView b, cArrayView x, double eps, int min_iterations, int max_iterations, TFunctor1 apply_preconditioner, TFunctor2 matrix_multiply, bool verbose=false)

template<typename TFunctor1 , typename TFunctor2 >
int	cgs_callbacks (const cArrayView b, cArrayView x, double eps, int min_iterations, int max_iterations, TFunctor1 apply_preconditioner, TFunctor2 matrix_multiply, bool verbose=false)
	CGS solver. More...

Function Documentation

template<typename TFunctor1 , typename TFunctor2 >

int bicgstab_callbacks	(	const cArrayView	b,
		cArrayView	x,
		double	eps,
		int	min_iterations,
		int	max_iterations,
		TFunctor1	apply_preconditioner,
		TFunctor2	matrix_multiply,
		bool	verbose = `false`
	)

Callback-based BiCGSTAB.

Bi-Conjugate gradients stabilized method.

Parameters

b	Right hand side.
x	Output vector. An initial guess may be present at beginning.
eps	Relative tolerance.
min_iterations	Minimal iterations count.
max_iterations	Maximal iterations count.
apply_preconditioner	Functor compatible with void(*)(const Array&, Array&) prototype. Should apply a custom preconditioner to a given vector.
matrix_multiply	Functor compatible with void(*)(const Array&, Array&) prototype. Should multiply the given vector by the matrix of the equation set.
verbose	Whether to comment the progress to stdout.

Returns: Iteration count.

template<class TArray , class TArrayView , class Preconditioner , class MatrixMultiplication , class NewArray = decltype(default_new_complex_array), class AxbyOperation = decltype(default_complex_axby), class ScalarProduct = decltype(operator|<Complex>), class ComputeNorm = decltype(default_compute_norm)>

unsigned cg_callbacks	(	const TArrayView	b,
		TArrayView	x,
		double	eps,
		unsigned	min_iterations,
		unsigned	max_iterations,
		Preconditioner	apply_preconditioner,
		MatrixMultiplication	matrix_multiply,
		bool	verbose = `true`,
		NewArray	new_array = `default_new_complex_array`,
		AxbyOperation	axby = `default_complex_axby`,
		ScalarProduct	scalar_product = `operator\|<Complex>`,
		ComputeNorm	compute_norm = `default_compute_norm`
	)

Callback-based conjugate gradients. There is a variety of template arguments and function parameters that aim at generality so that the function can be used with various implementations of array arithmetic. The numerically intensive sections are being computed by user-supplied routines. Also the array types have a template character; they are

TArray: A stand-alone array type that can be allocated. Has to support the methods "norm" (computation of 2-norm), "size" (length of the array) and "data" (pointer to the raw data).
TArrayView: Either a reference to TArray, or a different compatible type that supports the three listed methods. It is not necessary to be allocable.
NewArray: routine that allocates an array and possibly does something more, e.g. registers the array at the computing device (GPU). NewArray has to be compatible with the signature
* TArray (*NewArray)

*
Preconditioner: routine that

Parameters

b	Right hand side.
x	Output vector. An initial guess may be present at beginning.
eps	Relative tolerance.
min_iterations	Minimal iterations count.
max_iterations	Maximal iterations count.
apply_preconditioner	Functor compatible with the signature * void () (const TArrayView, TArrayView) Applies a custom preconditioner to the vector given as first argument and stores the result in the second argument.
matrix_multiply	Functor compatible with the signature * void () (const TArrayView, TArrayView) Multiplies the vector given in the first argument by the matrix of the equation set. The result will be stored in the second argument.
verbose	Whether to display progress information.
new_array	Functor compatible with the signature * TArray () (size_t) Allocates (and preprocesses, if needed) a new array of type TArray and returns a copy of the array. This can be useful when the new arrays need to be uploaded to a different computing device (mostly GPU).
axby	Functor compatible with the signature * void () (Complex a, const TArrayView x, Complex b, const TArrayView y) Stores the linear combination \( a\mathbf{x} + b\mathbf{y} \) into the array \( \mathbf{x} \).
scalar_product	Functor compatible with the signature * Complex () (const TArrayView x, const TArrayView y) Computes the scalar product (without complex conjugation), i.e. the sum \[ \sum_{i = 1}^N x_i y_i \ . \]
compute_norm	Functor compatible with signature * double () (const TArrayView x) Computes the norm of the array.

Returns: Iteration count.

template<typename TFunctor1 , typename TFunctor2 >

int cgs_callbacks	(	const cArrayView	b,
		cArrayView	x,
		double	eps,
		int	min_iterations,
		int	max_iterations,
		TFunctor1	apply_preconditioner,
		TFunctor2	matrix_multiply,
		bool	verbose = `false`
	)

Conjugate gradients squared,

Parameters

b	Right hand side.
x	Output vector. An initial guess may be present at beginning.
eps	Relative tolerance.
min_iterations	Minimal iterations count.
max_iterations	Maximal iterations count.
apply_preconditioner	Functor compatible with void(*)(const Array&, Array&) prototype. Should apply a custom preconditioner to a given vector.
matrix_multiply	Functor compatible with void(*)(const Array&, Array&) prototype. Should multiply the given vector by the matrix of the equation set.
verbose	Whether to comment the progress to stdout.

Returns: Iteration count.

void default_complex_axby	(	Complex	a,
		cArrayView	x,
		Complex	b,
		const cArrayView	y
	)

inline

Computes a linear combination of two vectors and stores the output in the first vector. This is a default implementation of the method. It can be substituted by another, if necessary; for example one could call specialized routine from BLAS or use a GPU kernel.

double default_compute_norm ( const cArrayView x )

inline

This routine is the default way of how to compute a norm of an object. It can be overloaded by some more sophisticated implementation (e.g. BLAS or OpenCL version).

cArray default_new_complex_array ( size_t n )

inline

Create (and return a copy of) a NumberArray<Complex> object. This is used as a default method of creating an array in cg_callbacks. It can be substituted by a different method, if necessary; for example when the created array needs to be registered at GPU first.

Functions

Function Documentation