 |
Hex
1.0
Hydrogen-electron collision solver
|
 |
Hex
1.0
Hydrogen-electron collision solver
|
#include <tuple>#include "arrays.h"#include "input.h"#include "matrix.h"#include "radial.h"#include "parallel.h"#include "opencl.h"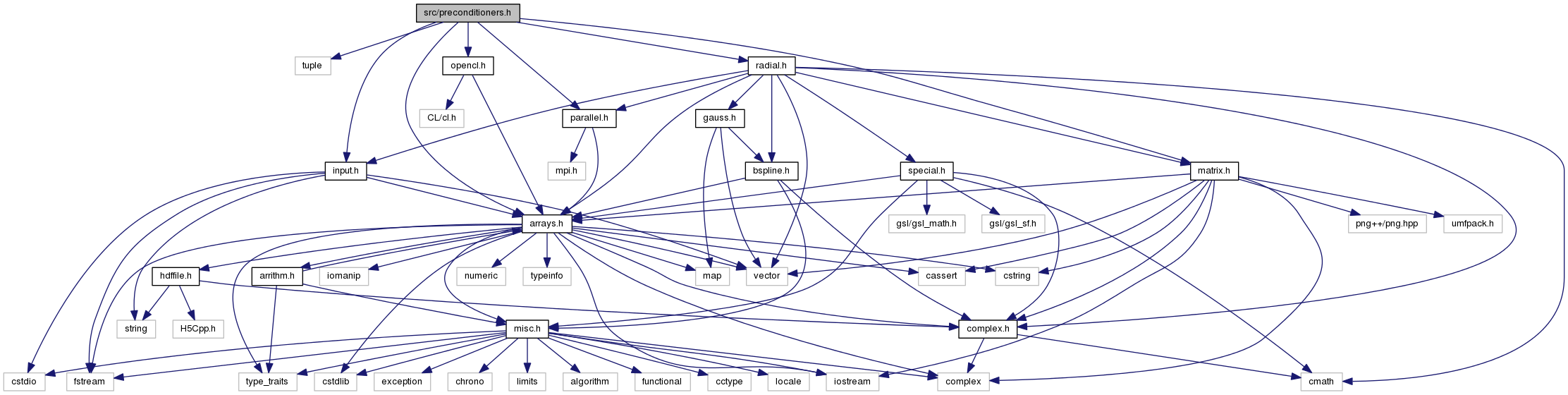
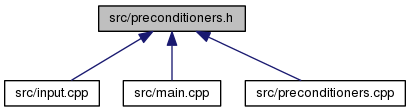
Go to the source code of this file.
Data Structures | |
| class | PreconditionerBase |
| Preconditioner template. More... | |
| class | NoPreconditioner |
| Solution driver without actual preconditioner. More... | |
| class | CGPreconditioner |
| CG iteration-based preconditioner. More... | |
| class | GPUCGPreconditioner |
| CG iteration-based preconditioner (GPU variant). More... | |
| class | JacobiCGPreconditioner |
| Jacobi-preconditioned CG-based preconditioner. More... | |
| class | SSORCGPreconditioner |
| SSOR-preconditioned CG-based preconditioner. More... | |
| class | ILUCGPreconditioner |
| ILU-preconditioned CG-based preconditioner. More... | |
| class | DICCGPreconditioner |
| DIC-preconditioned CG-based preconditioner. More... | |
| class | SPAICGPreconditioner |
| SPAI-preconditioned CG-based preconditioner. More... | |
| class | TwoLevelPreconditioner |
| Two-resolution preconditioner. More... | |
| class | MultiresPreconditioner |
| Multi-resolution (V-cycle) preconditioner. More... | |
| class | Preconditioners |
| Preconditioner traits. More... | |
Functions | |
| cArray | iChol (cArrayView const &A, lArrayView const &I, lArrayView const &P) |
| Sparse incomplete Cholesky decomposition. More... | |
| SymDiaMatrix | DIC (SymDiaMatrix const &A) |
| DIC preconditioner. More... | |
| SymDiaMatrix | SSOR (SymDiaMatrix const &A) |
| SSOR preconditioner. More... | |
| CooMatrix | SPAI (SymDiaMatrix const &A, const iArrayView diagonals) |
| SPAI preconditioner. More... | |
| SymDiaMatrix DIC | ( | SymDiaMatrix const & | A | ) |
Setup the diagonal incomplete Cholesky preconditioner. It is a essentially the original matrix with a preconditioned diagonal and the strict upper and lower triangles normalized by the preconditioned diagonal, i.e. a matrix
\[ \mathbf{P} = \mathbf{\tilde{L}}_\mathbf{A} + \mathbf{D}^{-1} + \mathbf{\tilde{L}}_\mathbf{A}^T \]
for the preconditioner
\[ \mathbf{M} = (\mathbf{D} + \mathbf{L}_\mathbf{A}) \mathbf{D}^{-1} (\mathbf{D} + \mathbf{U}_\mathbf{A}) = (1 + \mathbf{\tilde{U}}_\mathbf{A}^T) \mathbf{D} (1 + \mathbf{\tilde{U}}_\mathbf{A}) \]
The formula for the elements of \( \mathbf{D} \) is
\[ d_i = a_{ii} - \sum_{k < i} a_{ik} d_{k}^{-1} a_{ki} \ , \]
and is to be evaluated along the diagonal, re-using the just computed values \( d_i \). Hence, the access pattern in dense matrix would be
\[ \pmatrix { \ast & & & \ast & & \cr & \ast & & \ast & & \cr & & \ast & \ast & & \cr \ast & \ast & \ast & ? & & \cr & & & & & \cr & & & & & \cr } \]
In the case of the sparse SymDiaMatrix, the asterisks will occur only on the nonzero diagonals.
| A | Matrix in SymDiaMatrix format that is to be preconditioned. |
| cArray iChol | ( | cArrayView const & | A, |
| lArrayView const & | I, | ||
| lArrayView const & | P | ||
| ) |
This routine computes the LDL-decomposition of a symmetric matrix,
\[ A = L D L^T \ , \]
where \( L \) is a lower triangular matrix normalized so that it has units on the diagonal and \( D \) is a diagonal matrix.
| A | Matrix elements in the form of a consecutive array \( \left\{a_i\right\}_{i=1}^N \) as in \[ \pmatrix { a_1 & & & & \cr a_2 & a_3 & & & \cr a_4 & a_5 & a_6 & & \cr a_7 & a_8 & a_9 & a_{10} & \cr \vdots & & & & \ddots \cr } \] Whenever \( a_k \) is equal to zero, it is (or can be) omitted from the input array. |
| I | Array of column indices (one for every element of A). |
| P | Array of row pointers, i.e. starting positions of rows of A. For dense matrix it would be 0, 1, 3, 6, 10, ... The last element must be equal to the length of both A and I. |
| CooMatrix SPAI | ( | SymDiaMatrix const & | A, |
| const iArrayView | diagonals | ||
| ) |
Compute sparse aproximate inverse of a given symmetrix diagonal matrix A. The sparse structure of the SPAI is set by the second parameter that contains list of non-lower diagonal indices (greater than or equal to zero).
This function uses Lapack routine ZGELSD.
| SymDiaMatrix SSOR | ( | SymDiaMatrix const & | A | ) |
Symmetric successive over-relaxation preconditioner for \( \omega = 1 \). (Essentially symmetrized Gauss-Seidel). The resulting matrix contains normalized lower (and upper) triangle and in the place of the unit diagonal is the inverse diagonal of \( \mathbf{A} \). So, having the preconditioner
 1.8.5
1.8.5