bto_integrals_gbl Module Reference

This module contains routines to calculate the 1-electron integrals in the B-spline basis. More...

Functions/Subroutines
subroutine, public	BB_shell_integrals (shell_a, shell_b, starting_index_a, starting_index_b, a, max_property_l, property_center, symmetry_data, olap_column, kei_column, prop_column, nai_column, ecp_column, bbb_column, one_elham_column, int_index, integrals)
subroutine, public	BB_initialize (bspline_grid, max_bspline_l, max_prop_l, dipole_damp_factor, symmetry_data, rmat_radius, bto_shells, no_cgto_shells, shell_starting_indices)
	Calculates: r_points, weights, B_vals, temp_r, bspline_boundary_val, bspline_start_end, prop_on_grid, leg_on_grid, re_sph_harm_center.
subroutine, public	construct_bspline_quadrature_grid (knots, x, w, n, n_rng_knot, r_points, weights, n_total_points)
	Constructs a quadrature grid for the B-spline basis described by a given knot sequence. The final quadrature grid comprises effectively a series of quadratures over subintervals generated in between each pair of distinct knots.

Detailed Description

This module contains routines to calculate the 1-electron integrals in the B-spline basis.

Todo

Add checking that the radial quadratures have high enough order to get exact results. Integrals involving radial B-splines with a non-zero derivative at r=A (i.e. at the origin of the B-spline grid) are not evaluated.

Function/Subroutine Documentation

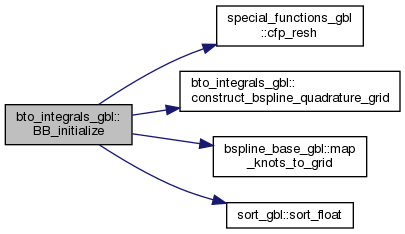
BB_initialize()

subroutine, public bto_integrals_gbl::BB_initialize	(	type(bspline_grid_obj), intent(inout)	bspline_grid,
		integer, intent(in), optional	max_bspline_l,
		integer, intent(in), optional	max_prop_l,
		real(kind=cfp), intent(in)	dipole_damp_factor,
		type(symmetry_obj), intent(in)	symmetry_data,
		real(kind=cfp), intent(in)	rmat_radius,
		type(bto_shell_data_obj), dimension(:), intent(in)	bto_shells,
		integer, intent(in)	no_cgto_shells,
		integer, dimension(:), intent(in)	shell_starting_indices )

Calculates: r_points, weights, B_vals, temp_r, bspline_boundary_val, bspline_start_end, prop_on_grid, leg_on_grid, re_sph_harm_center.

Here is the call graph for this function:

BB_shell_integrals()

subroutine, public bto_integrals_gbl::BB_shell_integrals	(	type(bto_shell_data_obj), intent(in), target	shell_a,
		type(bto_shell_data_obj), intent(in), target	shell_b,
		integer, intent(in)	starting_index_a,
		integer, intent(in)	starting_index_b,
		real(kind=cfp), intent(in)	a,
		integer, intent(in)	max_property_l,
		real(kind=cfp), dimension(3), intent(in)	property_center,
		type(symmetry_obj), intent(in)	symmetry_data,
		integer, intent(in)	olap_column,
		integer, intent(in)	kei_column,
		integer, intent(in)	prop_column,
		integer, intent(in)	nai_column,
		integer, intent(in)	ecp_column,
		integer, intent(in)	bbb_column,
		integer, intent(in)	one_elham_column,
		integer, dimension(:,:), allocatable	int_index,
		real(kind=cfp), dimension(:,:), allocatable	integrals )

Here is the call graph for this function:

construct_bspline_quadrature_grid()

subroutine, public bto_integrals_gbl::construct_bspline_quadrature_grid	(	real(kind=cfp), dimension(:), intent(in)	knots,
		real(kind=cfp), dimension(2*n+1), intent(in)	x,
		real(kind=cfp), dimension(2*n+1), intent(in)	w,
		integer, intent(in)	n,
		integer, intent(in)	n_rng_knot,
		real(kind=cfp), dimension(:), allocatable	r_points,
		real(kind=cfp), dimension(:), allocatable	weights,
		integer, intent(out)	n_total_points )

Constructs a quadrature grid for the B-spline basis described by a given knot sequence. The final quadrature grid comprises effectively a series of quadratures over subintervals generated in between each pair of distinct knots.