molecular_basis_gbl Module Reference

Functions/Subroutines
subroutine	add_shell (this, shell_data)
subroutine	print_energy_sorted_orbital_table (this)
subroutine	one_electron_integrals (this, integral_storage, integral_options)
subroutine	two_electron_integrals_sparse (this, integral_storage, integral_options)
	Transform atomic 2-electron integrals to molecular ones. More...
subroutine	fetch_atomic_integrals_block (this, ao_integrals, iblk, rbeg, Rn, Ri, Rv, skip2ec, block_offset)
	Copy atomic 2-electron integrals to a sparse array. More...
subroutine	sparse_from_dense (Sp, Sj, Sv, A)
	Extract non-zero elements from a dense matrix. More...
subroutine	transform_one_index (nAr, nAc, Ap, Aj, Av, nBr, nBc, Bp, Bj, Bv_beg, Bv, Cp, Cj, Cv, triangle, pyramid, blocksym, blockcnt, TA_orb, CA_orb, TB_orb, CB_orb, skip2ec, mo_mpi_redistribution)
	Multiplication of two sparse matrices (somewhat tweaked) More...
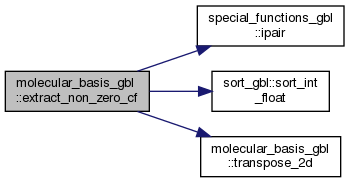
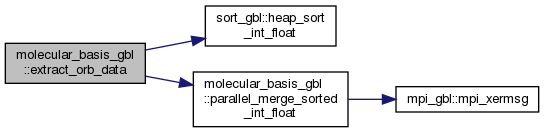
subroutine	extract_orb_data (T_orb, C_orb, nAr, nAc, Ap, A_T, A_C)
	Get special sparse matrix column pointers. More...
recursive subroutine	parallel_merge_sorted_int_float (nthreads, Ai, Bi, Ci, Af, Bf, Cf, As, Ae, Bs, Be, Cs, Ce, icol)
	Merge sorted indexed arrays. More...
subroutine	two_electron_integrals (this, integral_storage, integral_options)
integer function, dimension(size(bf_indices, 2))	integral_index (this, integral_type, bf_indices)
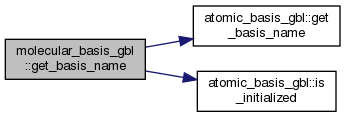
character(len=line_len) function	get_basis_name (this)
subroutine	delete_small_coefficients (this)
subroutine	delete_orbitals (this, symmetry, to_delete)
subroutine	transpose_2d (batch_in, batch_t, nrow, ncol)
	This routine transposes the 2D matrix on input while determining whether all elements of the array are zero. More...
subroutine	omp_two_p_transform_pqrs_block_to_ijrs_AO_is_local (ao_integrals, int_type, rs_start, rs_end, ij_type, iqrs, hlp, mobas, cf, cf_t, ijrs, no_ao, last_tgt_ao, no_int, no_pairs, rs_ind, two_p_continuum)
subroutine	omp_two_p_transform_pqrs_block_to_ijrs_AO_is_not_local (ao_integrals, int_type, rs_start, rs_end, ij_type, iqrs, hlp, mobas, cf, cf_t, ijrs, no_ao, last_tgt_ao, no_int, no_pairs, rs_ind, two_p_continuum)
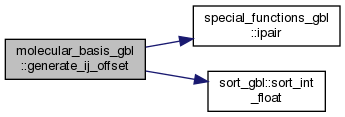
subroutine	generate_ij_offset (mobas, ij_type, ij_orbital_range, two_p_continuum, ij_offset, n_integrals)
subroutine	extract_non_zero_cf (cf_t, cf_t_non_zero, mo_indices, n_non_zero)
subroutine	bisect_index (val, ijkl_indices, col, last_index, ind, found)
subroutine	read_ijkl_indices (this, lunit, file_name, record_start, position_after_read)
subroutine	orbital_radial_charge_density (this, rmat_radius, A, B, delta_r, save_to_disk, charge_densities)
subroutine	eval_orbital (this, orb_i, r, n_points, orbital_at_r, sign_at_r)

Function/Subroutine Documentation

add_shell()

subroutine molecular_basis_gbl::add_shell	(	class(molecular_orbital_basis_obj)	this,
		class(shell_data_obj), intent(inout)	shell_data
	)

bisect_index()

subroutine molecular_basis_gbl::bisect_index	(	integer, intent(in)	val,
		integer, dimension(:,:), pointer	ijkl_indices,
		integer, intent(in)	col,
		integer, intent(in)	last_index,
		integer, intent(out)	ind,
		logical, intent(out)	found
	)

Here is the call graph for this function:

delete_orbitals()

subroutine molecular_basis_gbl::delete_orbitals	(	class(molecular_orbital_basis_obj)	this,
		integer, intent(in)	symmetry,
		logical, dimension(:), intent(in)	to_delete
	)

delete_small_coefficients()

subroutine molecular_basis_gbl::delete_small_coefficients

(

class(molecular_orbital_basis_obj)

this

)

eval_orbital()

subroutine molecular_basis_gbl::eval_orbital	(	class(molecular_orbital_basis_obj)	this,
		integer, intent(in)	orb_i,
		real(kind=cfp), dimension(3,n_points), intent(in)	r,
		integer, intent(in)	n_points,
		real(kind=cfp), dimension(:), allocatable	orbital_at_r,
		integer, dimension(:), allocatable	sign_at_r
	)

Here is the call graph for this function:

extract_non_zero_cf()

subroutine molecular_basis_gbl::extract_non_zero_cf	(	real(kind=cfp), dimension(:,:), allocatable	cf_t,
		real(kind=cfp), dimension(:,:), allocatable	cf_t_non_zero,
		integer, dimension(:,:), allocatable	mo_indices,
		integer, dimension(:), allocatable	n_non_zero
	)

Here is the call graph for this function:

extract_orb_data()

subroutine molecular_basis_gbl::extract_orb_data	(	integer, dimension(9), intent(in)	T_orb,
		integer, dimension(9), intent(in)	C_orb,
		integer, intent(in)	nAr,
		integer, intent(in)	nAc,
		integer, dimension(:), allocatable	Ap,
		integer, dimension(9), intent(out)	A_T,
		integer, dimension(9), intent(out)	A_C
	)

Get special sparse matrix column pointers.

Author

Jakub Benda

Date

2018

Constructs two sets of column pointers: One pointing to the first column corresponding to the first molecular orbital in every symmetry, the other pointing to the first continuum molecular orbital in every symmetry.

Parameters

T_orb	Absolute index of the first molecular orbital per symmetry.
C_orb	Absolute index of the first continuum molecular orbital per symmetry.
nAr	Number of rows in Ai.
nAc	Number of columns in Ai (must be equal to the total number of molecular orbitals).
An	Number of elements in Ai.
A_T	On output, positions in Ai of the column corresponding to the first molecular orbital per symmetry.
A_C	On output, positions in Ai of the column corresponding to the first continuum molecular orbital per symmetry.

Here is the call graph for this function:

fetch_atomic_integrals_block()

subroutine molecular_basis_gbl::fetch_atomic_integrals_block	(	class(molecular_orbital_basis_obj)	this,
		type(p2d_array_obj), pointer	ao_integrals,
		integer, intent(in)	iblk,
		integer, intent(inout)	rbeg,
		integer, intent(out)	Rn,
		integer, dimension(:,:), allocatable	Ri,
		real(kind=cfp), dimension(:,:), intent(inout)	Rv,
		logical, intent(in)	skip2ec,
		integer, dimension(:), optional, allocatable	block_offset
	)

Copy atomic 2-electron integrals to a sparse array.

Authors

Jakub Benda, Zdenek Masin

Date

2018, 2020

Retrieve all [pq|rs] atomic integrals for given block index (ie. for given p,q). Write them into the supplied (pre-allocated) arrays Ri(:), Rv(:) as elements of sparse 4-index tensor; Ri(:) will contains rectangular zero-based multi-indices of the non-zero elements, Rv(:) will contain the values of the integrals.

Parameters

this	Reference to the parent type.
ao_integrals	Pointer to the p2d_array_obj structure where the AO integrals are stored
iblk	Zero-based rectangular multi-index of the block to retrive.
rbeg	Starting index for arrays Ri, Rv. In case block_offset is present this value has the meaning of the offset for storage of the integrals in the Rv array which is gradually accumulated in the main loop over iblk.
Rn	On return, number of elements written into the arrays Rv and Ri.
Ri	Zero-based multi-index for each element in Rv.
Rv	Array of non-zero atomic two-electron integrals.
skip2ec	Whether to skip [CC|CT] and [CC|CC] integrals (mostly .TRUE.).
block_offset	If present then the integrals from ao_integrals are copied to the block_offset, and Rv arrays in the blocked storage format used in case of nprocs > 1. In this case it is required that the ao_integrals are also stored in the block format. The array Ri is not touched at all (may be unallocated on input).

Here is the call graph for this function:

generate_ij_offset()

subroutine molecular_basis_gbl::generate_ij_offset	(	class(molecular_orbital_basis_obj)	mobas,
		integer(kind=1), dimension(:)	ij_type,
		integer, dimension(:,:), allocatable	ij_orbital_range,
		logical, intent(in)	two_p_continuum,
		integer, dimension(:), allocatable	ij_offset,
		integer, intent(out)	n_integrals
	)

Here is the call graph for this function:

get_basis_name()

character(len=line_len) function molecular_basis_gbl::get_basis_name

(

class(molecular_orbital_basis_obj)

this

)

Here is the call graph for this function:

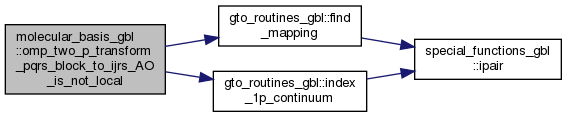
integral_index()

integer function, dimension(size(bf_indices,2)) molecular_basis_gbl::integral_index	(	class(molecular_orbital_basis_obj)	this,
		character(len=*), intent(in)	integral_type,
		integer, dimension(:,:), intent(in)	bf_indices
	)

Here is the call graph for this function:

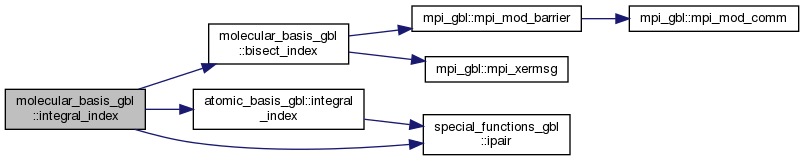
omp_two_p_transform_pqrs_block_to_ijrs_AO_is_local()

subroutine molecular_basis_gbl::omp_two_p_transform_pqrs_block_to_ijrs_AO_is_local	(	type(p2d_array_obj), intent(inout)	ao_integrals,
		integer, intent(in)	int_type,
		integer, intent(in)	rs_start,
		integer, intent(in)	rs_end,
		integer(kind=1), dimension(:), allocatable	ij_type,
		real(kind=cfp), dimension(:,:), allocatable	iqrs,
		real(kind=cfp), dimension(:), allocatable	hlp,
		class(molecular_orbital_basis_obj), intent(in)	mobas,
		real(kind=cfp), dimension(:,:), allocatable	cf,
		real(kind=cfp), dimension(:,:), allocatable	cf_t,
		real(kind=cfp), dimension(:,:), allocatable	ijrs,
		integer, intent(in)	no_ao,
		integer, intent(in)	last_tgt_ao,
		integer, intent(inout)	no_int,
		integer, intent(in)	no_pairs,
		integer, dimension(2,no_pairs), intent(in)	rs_ind,
		logical, intent(in)	two_p_continuum
	)

Warning

Note that the use of the 'allocatable' attribute for the argument arrays is key for performance since this attribute allows the compiler to assume that the arrays are contiguous in memory. Alternatively the 'contiguous' attribute can be used but it is a F2008 feature so we omit it here. It is assumed that the threads have been launched outside of this routine.

omp_two_p_transform_pqrs_block_to_ijrs_AO_is_not_local()

subroutine molecular_basis_gbl::omp_two_p_transform_pqrs_block_to_ijrs_AO_is_not_local	(	type(p2d_array_obj), intent(inout)	ao_integrals,
		integer, intent(in)	int_type,
		integer, intent(in)	rs_start,
		integer, intent(in)	rs_end,
		integer(kind=1), dimension(:), allocatable	ij_type,
		real(kind=cfp), dimension(:,:), allocatable	iqrs,
		real(kind=cfp), dimension(:), allocatable	hlp,
		class(molecular_orbital_basis_obj), intent(in)	mobas,
		real(kind=cfp), dimension(:,:), allocatable	cf,
		real(kind=cfp), dimension(:,:), allocatable	cf_t,
		real(kind=cfp), dimension(:,:), allocatable	ijrs,
		integer, intent(in)	no_ao,
		integer, intent(in)	last_tgt_ao,
		integer, intent(inout)	no_int,
		integer, intent(in)	no_pairs,
		integer, dimension(:,:), allocatable	rs_ind,
		logical, intent(in)	two_p_continuum
	)

Warning

Note that the use of the 'allocatable' attribute for the argument arrays is key for performance since this attribute allows the compiler to assume that the arrays are contiguous in memory. Alternatively the 'contiguous' attribute can be used but it is a F2008 feature so we omit it here. It is assumed that the threads have been launched outside of this routine.

Here is the call graph for this function:

one_electron_integrals()

subroutine molecular_basis_gbl::one_electron_integrals	(	class(molecular_orbital_basis_obj)	this,
		class(integral_storage_obj), intent(inout)	integral_storage,
		class(integral_options_obj), intent(in)	integral_options
	)

Here is the call graph for this function:

orbital_radial_charge_density()

subroutine molecular_basis_gbl::orbital_radial_charge_density	(	class(molecular_orbital_basis_obj)	this,
		real(kind=cfp), intent(in)	rmat_radius,
		real(kind=cfp), intent(in)	A,
		real(kind=cfp), intent(in)	B,
		real(kind=cfp), intent(in)	delta_r,
		logical, intent(in)	save_to_disk,
		real(kind=cfp), dimension(:,:), allocatable	charge_densities
	)

Here is the call graph for this function:

parallel_merge_sorted_int_float()

recursive subroutine molecular_basis_gbl::parallel_merge_sorted_int_float	(	integer, intent(in)	nthreads,
		integer, dimension(:,:), allocatable	Ai,
		integer, dimension(:,:), allocatable	Bi,
		integer, dimension(:,:), allocatable	Ci,
		real(cfp), dimension(:,:), allocatable	Af,
		real(cfp), dimension(:,:), allocatable	Bf,
		real(cfp), dimension(:,:), allocatable	Cf,
		integer, intent(in)	As,
		integer, intent(in)	Ae,
		integer, intent(in)	Bs,
		integer, intent(in)	Be,
		integer, intent(in)	Cs,
		integer, intent(in)	Ce,
		integer, intent(in)	icol
	)

Merge sorted indexed arrays.

Author

Jakub Benda

Date

2018

Merge two sorted integer arrays, and also corresponding real arrays. Uses the given number of threads.

Parameters

nthreads	Number of OpenMP threads to use.
Ai	First integer array to merge.
Bi	Second integer array to merge.
Ci	Destination integer array (combined length of Ai, Bi).
Af	First real array to merge.
Bf	Second real array to merge.
Cf	Destination real array (combined length of Af, Bf).
As,Ae	Indices defining sections of the arrays Ai,Af to use: Ai(As:Ae), Af(As:Ae).
Bs,Be	Indices defining sections of the arrays Bi,Bf to use: Bi(Bs:Be), Bf(Bs:Be).
Cs,Ce	Indices defining sections of the arrays Ci,Cf to use: Ci(Cs:Ce), Cf(Cs:Ce).

Here is the call graph for this function:

print_energy_sorted_orbital_table()

subroutine molecular_basis_gbl::print_energy_sorted_orbital_table

(

class(molecular_orbital_basis_obj)

this

)

Here is the call graph for this function:

read_ijkl_indices()

subroutine molecular_basis_gbl::read_ijkl_indices	(	class(molecular_orbital_basis_obj)	this,
		integer, intent(in)	lunit,
		character(len=*)	file_name,
		integer, intent(in)	record_start,
		integer, intent(out)	position_after_read
	)

sparse_from_dense()

subroutine molecular_basis_gbl::sparse_from_dense	(	integer, dimension(:), intent(out), allocatable	Sp,
		integer, dimension(:), intent(out), allocatable	Sj,
		real(kind=cfp), dimension(:), intent(out), allocatable	Sv,
		real(kind=cfp), dimension(:,:), intent(in), allocatable	A
	)

Extract non-zero elements from a dense matrix.

Authors

Jakub Benda

Date

2018

Given a dense matrix A, copy its non-zero elements into the array Sv, with corresponding CSC indices in Sp and Sj.

Parameters

Sp	Index of the first element in Sj/Sv in the given column. If two consecutive elements in Sp have the same value, it means that the column has zero length.
Sj	Row index of the corresponding element in Sv.
Sv	Non-zero elements of A.
A	Dense matrix (column major storage).

Here is the call graph for this function:

transform_one_index()

subroutine molecular_basis_gbl::transform_one_index	(	integer, intent(in)	nAr,
		integer, intent(in)	nAc,
		integer, dimension(:), allocatable	Ap,
		integer, dimension(:), allocatable	Aj,
		real(kind=cfp), dimension(:), allocatable	Av,
		integer, intent(in)	nBr,
		integer, intent(in)	nBc,
		integer, dimension(:), allocatable	Bp,
		integer, dimension(:,:), allocatable	Bj,
		integer, intent(in)	Bv_beg,
		real(kind=cfp), dimension(:,:), allocatable	Bv,
		integer, dimension(:), allocatable	Cp,
		integer, dimension(:,:), allocatable	Cj,
		real(kind=cfp), dimension(:,:), allocatable	Cv,
		logical, intent(in)	triangle,
		integer, intent(in)	pyramid,
		integer, intent(in)	blocksym,
		integer, intent(in)	blockcnt,
		integer, dimension(9), intent(in)	TA_orb,
		integer, dimension(9), intent(in)	CA_orb,
		integer, dimension(9), intent(in)	TB_orb,
		integer, dimension(9), intent(in)	CB_orb,
		logical, intent(in)	skip2ec,
		logical, intent(in)	mo_mpi_redistribution
	)

Multiplication of two sparse matrices (somewhat tweaked)

Authors

Jakub Benda

Date

2018

Multiply two sparse matrices, producing a sparse matrix as a result.

The subroutine allows restricting the operation to some elements to allow making use of the index symmetries of two-particle integrals:

• If "triangle" is true, then only a triangular part of the resulting matrix will be computed.
• If "pyramid" is non-negative, then only multi-indices smaller than the given value will be computed.

If both the above are true, which indicates the second stage of transformation, ie. (kl|pq] -> (kl|ij), then also:

• Skip combinations of orbitals with incompatible symmetries. The integral can be only nonzero when the overall symmetry of the four orbitals is totally symmetric.
• If "skip2ec" is true, do not calculate molecular integrals of CCCC and CCCT types.

Parameters

nAr	Number of rows in A (leading dimension).
nAc	Number of cols in A (the other dimension).
Ap	Positions in Av of the first element of each column of A.
Aj	Row indices corresponding to elements in Av.
Av	Non-zero elements of the matrix A.
nBr	Number of rows in B (leading dimension).
nBc	Number of cols in B (the other dimension).
Bp	Positions in Bv of the first element of each column of B.
Bj	Row indices corresponding to elements in Bv.
Bv_beg	Starting index in array Bv.
Bv	Non-zero elements of the matrix B.
Cp	On return, Positions in Cv of the first element of each column of C.
Cj	Row indices corresponding to elements in Cv.
Cv	Non-zero elements of the sparse matrix product.
Ci	Zero-based multi-indices corresponding to the elements of Cv.
triangle	Calculate only a triangular subset of C.
pyramid	Further restriction on calculated elements of C (limit on multi-index).
blocksym	Combined symmetry of the other pair of orbitals.
blockcnt	CC/CT/TT (= 2/1/0) type of the other pair of orbitals.
TA_orb	Helper array with the index of the first orbital per symmetry. Corresponds to column index of A.
CA_orb	Helper array with the index of the first continuum orbital per symmetry. Corresponds to column index of A.
TB_orb	Helper array with the index of the first orbital per symmetry. Corresponds to column index of B.
CB_orb	Helper array with the index of the first continuum orbital per symmetry. Corresponds to column index of B.
skip2ec	Whether to skip CCCC and CCCT combinations of molecular orbitals.
mo_mpi_redistribution	Whether to cyclically redistribute pairs of columns 'AB' over MPI tasks.

Here is the call graph for this function:

transpose_2d()

subroutine molecular_basis_gbl::transpose_2d	(	real(kind=cfp), dimension(:,:), allocatable	batch_in,
		real(kind=cfp), dimension(:,:), allocatable	batch_t,
		integer, intent(in)	nrow,
		integer, intent(in)	ncol
	)

This routine transposes the 2D matrix on input while determining whether all elements of the array are zero.

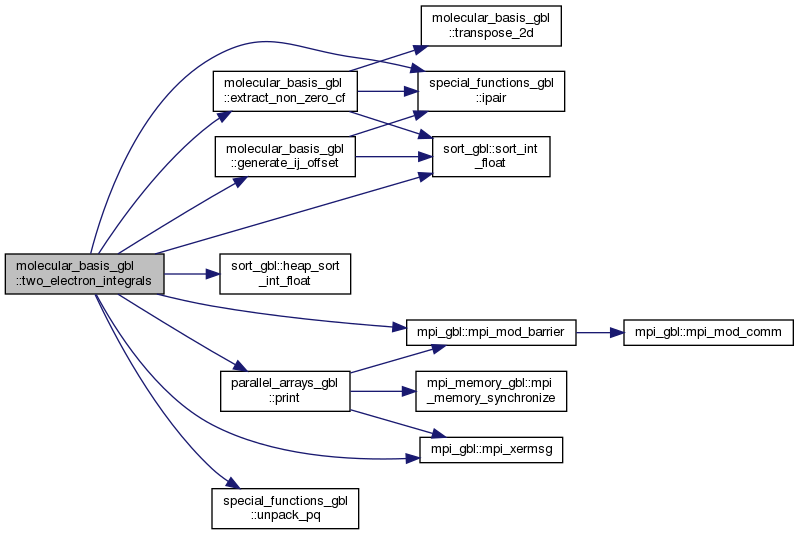
two_electron_integrals()

subroutine molecular_basis_gbl::two_electron_integrals	(	class(molecular_orbital_basis_obj)	this,
		class(integral_storage_obj), intent(inout)	integral_storage,
		class(integral_options_obj), intent(in)	integral_options
	)

Here is the call graph for this function:

two_electron_integrals_sparse()

subroutine molecular_basis_gbl::two_electron_integrals_sparse	(	class(molecular_orbital_basis_obj)	this,
		class(integral_storage_obj), intent(inout)	integral_storage,
		class(integral_options_obj), intent(in)	integral_options
	)

Transform atomic 2-electron integrals to molecular ones.

Authors

Jakub Benda

Date

2018

Calculates the molecular-orbital 2-electron integrals (ij|kl) from the known atomic-orbital 2-electron integrals [pq|rs]. The algorithm proceeds in several steps:

1. Expand all atomic integrals to a working array, including all those redundant in the sense of index symmetries.
2. Sort the integral array so that all integrals with common p,q are clustered together, resulting in a sequence of sparse matrices whose elements are indexed by atomic indices r,s.
3. Transform both indices of these sparse matrices to molecular ones by application of the expansion coefficient matrices, yielding object [pq|kl).
4. Sort the integral array again, but now group together elements with the same k,l, resulting in a sequence of sparse matrices whose elements are indexed by atomic indices p,q. Symbolically: (kl|pq].
5. Transform both indices p,q by application of the coefficient matrices, yielding (kl|ij).
6. Finally, sort the integrals to satisfy expectations of the library.

In the present implementation, steps 1, 2 and 3 are fused to avoid large memory use; only a few blocks are expanded at a time.

Some work can be saved with the knowledge of index and orbital symmetries:

• In the step 1 discard CCCC and CCCT types if not needed.
• In the step 3 it is possible to calculate the numbers [pq|kl) just for k >= l, due to symmetry k <-> l. In addition to this, the CCCC and CCCT combinations can be ignored if two electrons in continuum are not required.
• In the step 5 it is possible to used the same, ignoring anything else than i >= j, and one can skip also all i,j pairs, whose combined orbital symmetry is different than the combined orbital symmetry of the pair k,l. This is due to the fact that the product of the two pairs i,j and k,l must be totally symmetric. Furthermore, one can skip all i,j pairs that violate [ij] >= [kl], due to the symmetry i,j <-> k,l. Here [ij] is the standard triangular multi-index function. Again, as before, CCCC and CCCT combination can be skipped.

Note that this subroutine uses rectangular indexing function and transforms the indices to the triangular ones only at the very end.

Here is the call graph for this function: