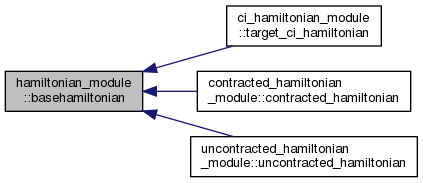
This is an abstract class that contains the majority of functionality required to construct hamiltonians. More...
Public Member Functions | |
| procedure, public | construct => construct_base_hamiltonian |
| procedure(generic_build), deferred | build_hamiltonian |
| procedure, public | slater_rules |
| procedure, public | evaluate_integrals |
| procedure, public | evaluate_integrals_singular |
| procedure, public | my_job |
Public Attributes | |
| class(orbitaltable), pointer | orbitals |
| Our orbitals required to generate symblic elements. More... | |
| class(options), pointer | options |
| Scatci program settings. More... | |
| class(baseintegral), pointer | integral |
| The integrals we are using. More... | |
| class(csfobject), dimension(:), pointer | csfs |
| Our configuration state functions. More... | |
| integer | nflg = 0 |
| integer | diagonal_flag |
| integer | positron_flag |
| Positron aware flag. More... | |
| integer | phase_flag |
| whether to evaluate integrals whilst dealing with phase More... | |
| logical | constructed = .false. |
| Has the hamiltonain been constructed. More... | |
| logical | initialized = .false. |
| Has the hamiltonian been initialized. More... | |
| integer | job_id = 0 |
| Whose job it is to (soon to be deprecated) More... | |
| integer | number_of_integrals = 0 |
| How many integrals have been evaluated? More... | |
| real(wp) | element_one = 0.0 |
| First element for idiag = 0. More... | |
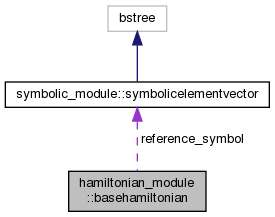
| type(symbolicelementvector) | reference_symbol |
| Symbols for idiag = 0. More... | |
Private Member Functions | |
| procedure, private | handle_two_pair |
| procedure, private | handle_one_pair |
| procedure, private | handle_same |
Detailed Description
This is an abstract class that contains the majority of functionality required to construct hamiltonians.
- Date
- 2017
This class provides an abstraction of a lot of the components required to build the hamiltonian. For example, the user does not need to worry about the specific implementation of Slaters rules or evaluating integrals this class wraps these features for you and should allow one to implement hamiltonians closer to those described in papers. This is not a Matrix class. BaseHamiltonain deals with building the matrix whilst BaseMatrix deals with storing the matrix.
Definition at line 57 of file Hamiltonian_module.f90.
Member Function/Subroutine Documentation
◆ build_hamiltonian()
| procedure(generic_build), deferred hamiltonian_module::basehamiltonian::build_hamiltonian |
Definition at line 77 of file Hamiltonian_module.f90.
◆ construct()
| procedure, public hamiltonian_module::basehamiltonian::construct |
Definition at line 76 of file Hamiltonian_module.f90.
◆ evaluate_integrals()
| procedure, public hamiltonian_module::basehamiltonian::evaluate_integrals |
Definition at line 82 of file Hamiltonian_module.f90.
◆ evaluate_integrals_singular()
| procedure, public hamiltonian_module::basehamiltonian::evaluate_integrals_singular |
Definition at line 83 of file Hamiltonian_module.f90.
◆ handle_one_pair()
|
private |
Definition at line 88 of file Hamiltonian_module.f90.
◆ handle_same()
|
private |
Definition at line 89 of file Hamiltonian_module.f90.
◆ handle_two_pair()
|
private |
Definition at line 87 of file Hamiltonian_module.f90.
◆ my_job()
| procedure, public hamiltonian_module::basehamiltonian::my_job |
Definition at line 90 of file Hamiltonian_module.f90.
◆ slater_rules()
| procedure, public hamiltonian_module::basehamiltonian::slater_rules |
Definition at line 80 of file Hamiltonian_module.f90.
Member Data Documentation
◆ constructed
| logical hamiltonian_module::basehamiltonian::constructed = .false. |
Has the hamiltonain been constructed.
Definition at line 67 of file Hamiltonian_module.f90.
◆ csfs
| class(csfobject), dimension(:), pointer hamiltonian_module::basehamiltonian::csfs |
Our configuration state functions.
Definition at line 61 of file Hamiltonian_module.f90.
◆ diagonal_flag
| integer hamiltonian_module::basehamiltonian::diagonal_flag |
Definition at line 64 of file Hamiltonian_module.f90.
◆ element_one
| real(wp) hamiltonian_module::basehamiltonian::element_one = 0.0 |
First element for idiag = 0.
Definition at line 71 of file Hamiltonian_module.f90.
◆ initialized
| logical hamiltonian_module::basehamiltonian::initialized = .false. |
Has the hamiltonian been initialized.
Definition at line 68 of file Hamiltonian_module.f90.
◆ integral
| class(baseintegral), pointer hamiltonian_module::basehamiltonian::integral |
The integrals we are using.
Definition at line 60 of file Hamiltonian_module.f90.
◆ job_id
| integer hamiltonian_module::basehamiltonian::job_id = 0 |
Whose job it is to (soon to be deprecated)
Definition at line 69 of file Hamiltonian_module.f90.
◆ nflg
| integer hamiltonian_module::basehamiltonian::nflg = 0 |
Definition at line 63 of file Hamiltonian_module.f90.
◆ number_of_integrals
| integer hamiltonian_module::basehamiltonian::number_of_integrals = 0 |
How many integrals have been evaluated?
Definition at line 70 of file Hamiltonian_module.f90.
◆ options
| class(options), pointer hamiltonian_module::basehamiltonian::options |
Scatci program settings.
Definition at line 59 of file Hamiltonian_module.f90.
◆ orbitals
| class(orbitaltable), pointer hamiltonian_module::basehamiltonian::orbitals |
Our orbitals required to generate symblic elements.
Definition at line 58 of file Hamiltonian_module.f90.
◆ phase_flag
| integer hamiltonian_module::basehamiltonian::phase_flag |
whether to evaluate integrals whilst dealing with phase
Definition at line 66 of file Hamiltonian_module.f90.
◆ positron_flag
| integer hamiltonian_module::basehamiltonian::positron_flag |
Positron aware flag.
Definition at line 65 of file Hamiltonian_module.f90.
◆ reference_symbol
| type(symbolicelementvector) hamiltonian_module::basehamiltonian::reference_symbol |
Symbols for idiag = 0.
Definition at line 73 of file Hamiltonian_module.f90.
The documentation for this type was generated from the following file:
- /home/jakub/Dokumenty/codes/ukrmol-in-git/source/mpi-ci-diag/Modules/Hamiltonian/Hamiltonian_module.f90