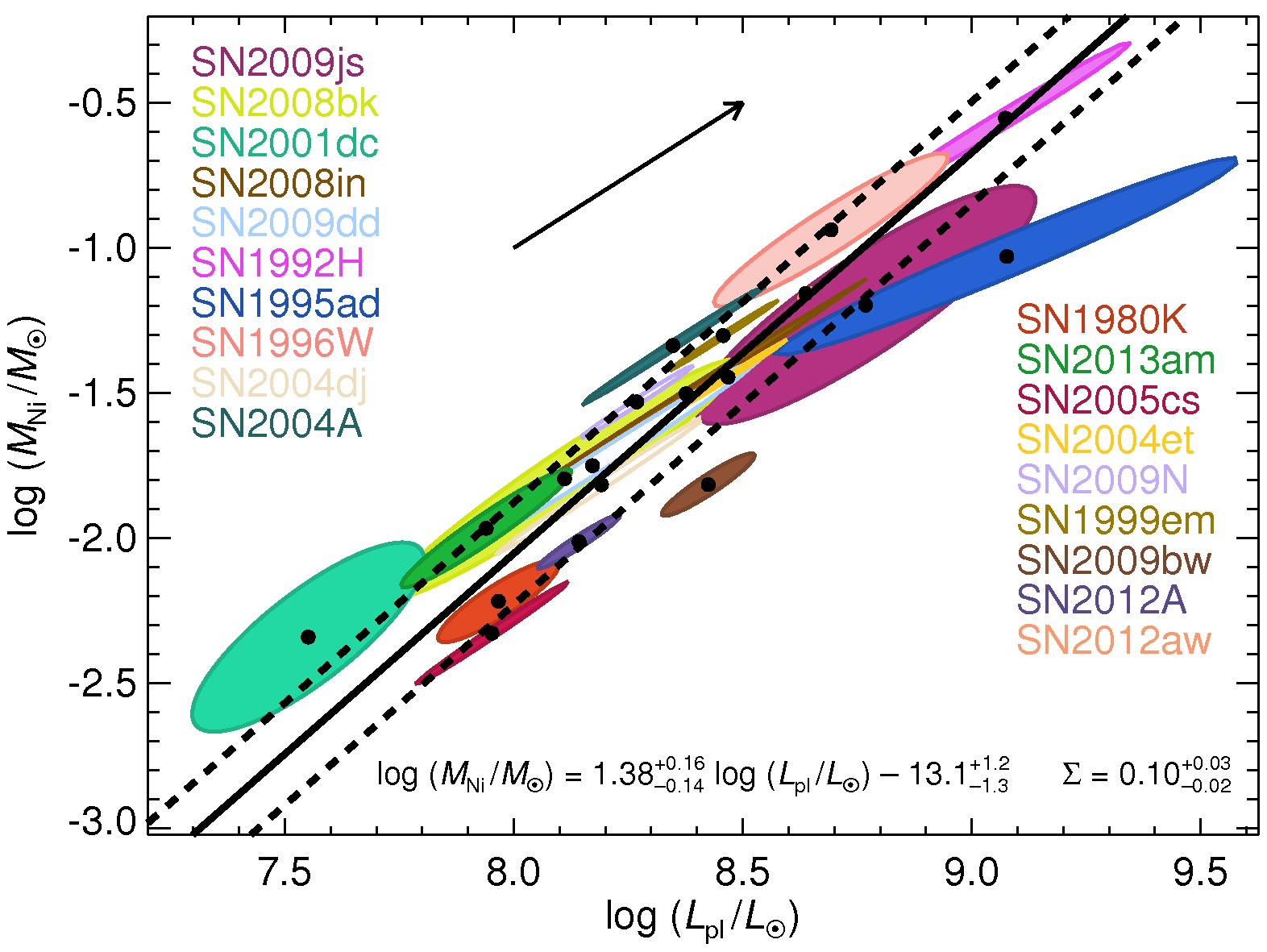
Physical parameters of Type II-Plateau Supernovae from Pejcha & Prieto (2015, ApJ, 806, 225)
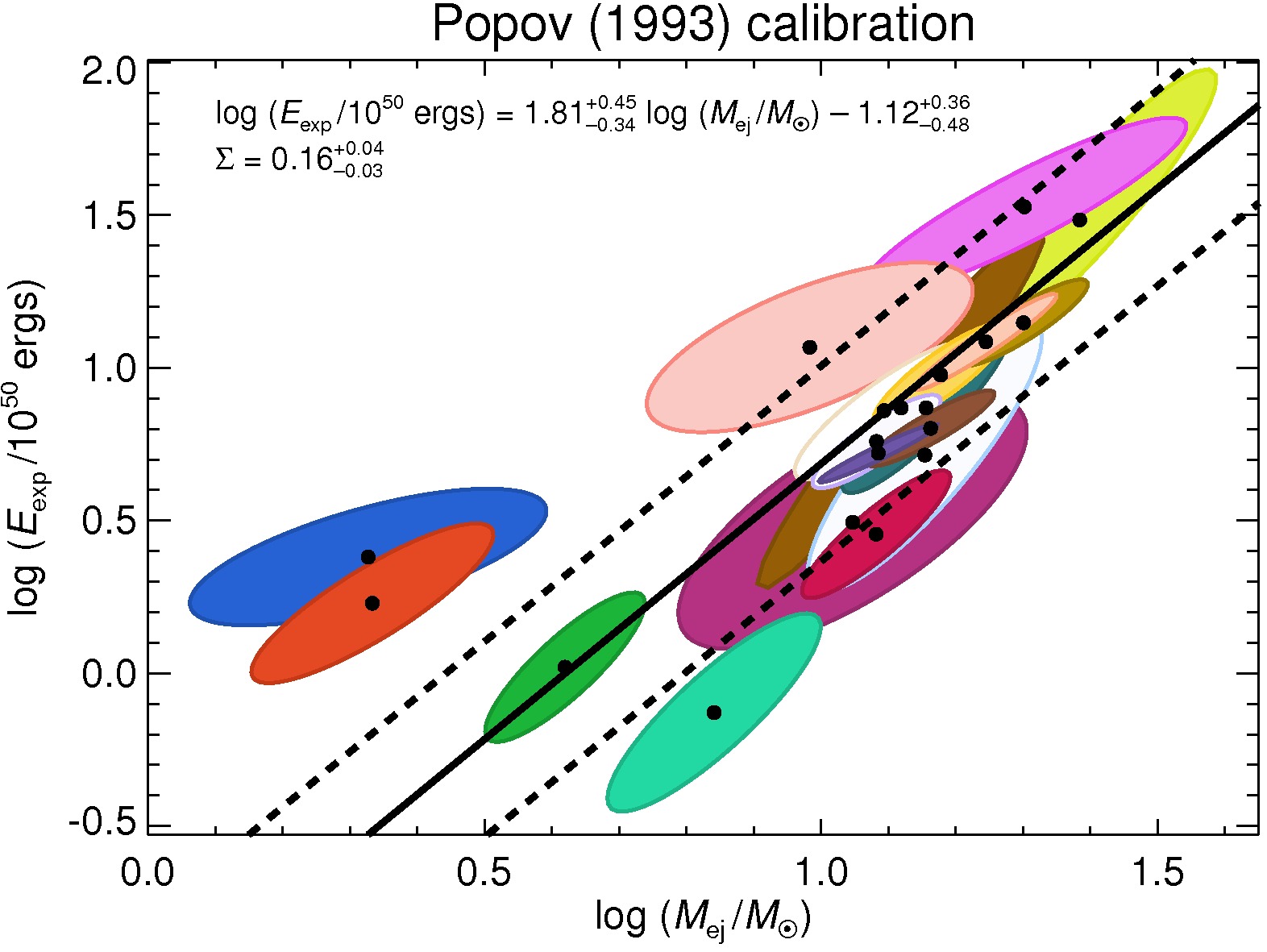
 |
Physical parameters of Type II-Plateau Supernovae from Pejcha & Prieto (2015, ApJ, 806, 225) |
 |
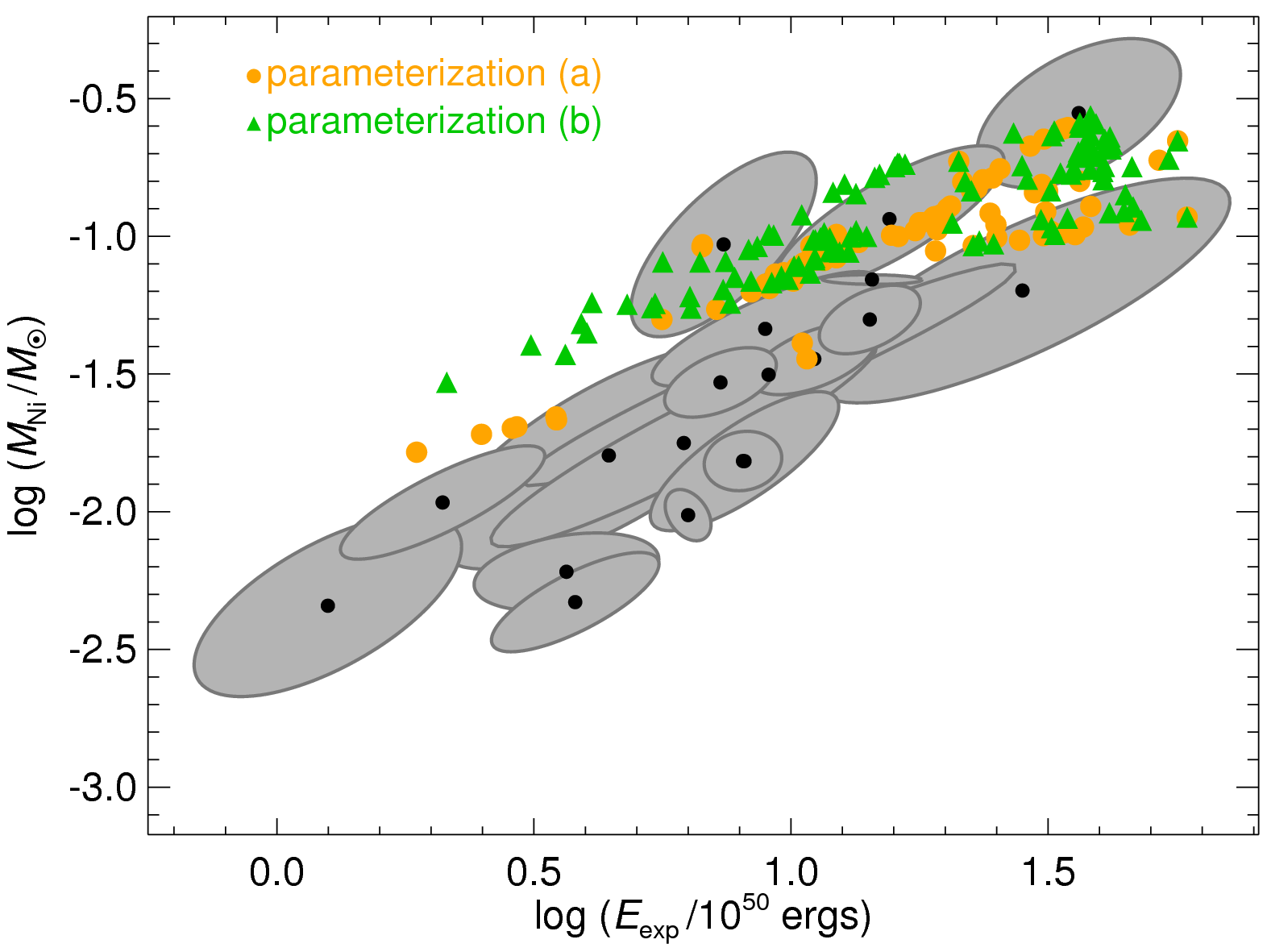 |
| Comparison of observational results from Pejcha & Prieto (2015, ApJ, 806, 225) shown with grey ellipses with the predictions of the neutrino mechanism from Pejcha & Thompson (2015, ApJ, 801, 90) shown with orange and green symbols. |
Here we give the plateau luminosities, nickel masses, explosion energies, and progenitor radii obtained using scaling relations from light curves fitted with the method of Pejcha & Prieto (2015, ApJ, 799, 215).
Litvinova & Nadezhin (1985) calibration of the scaling relations
Popov (1993) calibration of the scaling relations
Identification of supernova names
The column structure of the first two files is:
Sample IDL code to plot confidence ellipsoids like in our paper. covar is an array of covariance matrix coefficients obtained by reading the files above:
plot1 = 2 ; variables to plot, here M_Ni vs E_exp plot2 = 0 cov = reform(covar, 5,5) my_cov[0,0] = cov[plot1,plot1] my_cov[0,1] = cov[plot1,plot2] my_cov[1,0] = cov[plot2,plot1] my_cov[1,1] = cov[plot2,plot2] invc = invert(my_cov,/double) r2 = 2.30/(invc[0,0]*cp^2 + 2.0*invc[0,1]*cp*sp + invc[1,1]*sp^2) ;; factor 2.30 is related to number of variables and confidence level and is explained in Numerical Recipes r = sqrt(r2) x = r*cp ;; these are x and y coordinates of the 1-sigma confidence elipsoid relative to the datapoint y = r*sp