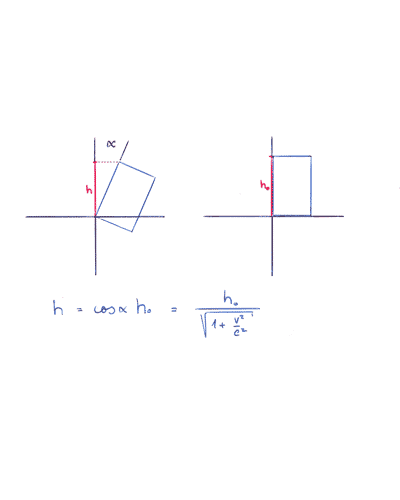Relativistický popis

Časové intervaly

Zmínili jsme se, že prostoročas je `vybaven' Minkowského geometrií. Ta nám umožní určit časové úseky a vzdálenosti nezávisle na tom, v které soustavě situaci popisujeme. Nejdříve si však musíme ujasnit, co pod měřením časových úseků a délek rozumíme.

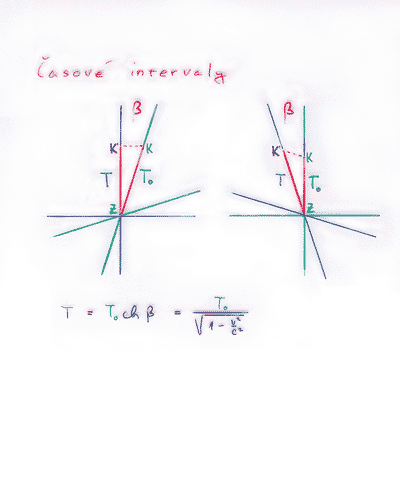
Zkoumejme dvě události Z a K, které se odehrály v letící raketě. Z hlediska pozorovatelky na raketě je jasné, co časový úsek mezi oběma událostmi znamená. Události se totiž z jejího hlediska staly na stejném místě a stačí jí tak pouze odečíst dobu T_o na svých ideálních hodinách – tento údaj nazýváme vlastní (klidový) čas mezi Z a K.

Pozorovatel na Zemi však chce časový úsek mezi Z a K změřit na svých hodinách. Raketa se ale vůči Zemi pohybuje a události Z a K se nestaly z hlediska pozemského pozorovatele na stejném místě. Jediné, co může pozorovatel udělat, je změřit dobu T mezi Z a okamžikem K', který se stal na stejném místě jako Z a je s K současný. Současný samozřejmě z hlediska pozorovatele na Zemi.

Pozorovatel na Zemi tak měří jakýsi průmět časového úseku ZK do své časové osy. Není tedy divu, že oba pozorovatelé naměří různé hodnoty – měří jiné veličiny!

Vztah mezi T_o a T je dán Minkowského trigonometrií obdobnou té obyčejné, rovinné. Jen místo funkce cos je nutno použít hypergoniometrickou funkci ch. Po vyjádření rapidity β pomocí rychlosti dostaneme známý vzorec pro prodlužování času.

Relativistické měření časových intervalů je tak přímá paralela s žížalím měření výšek. Různě skloněné žížaly měří různé průměty žížaly do své vertikální osy a naměří tak různé hodnoty. Pokud jsou žížaly od sebe odkloněny jen nepatrně, rozdíly ve výšce jsou zanedbatelné. Stejně tak při běžných rychlostech rozdíly v časových údajích měřenými různými pozorovateli nepozorujeme.