- boost 52, 55, 56, 57
- hypergoniometrické (hyperbolické) funkce 52, 53, 55
- inerciální soustava 27, 28, 32, 42, 47, 49, 50, 52, 53, 54, 55, 56, 57
- invariant Minkowského geometrie 50, 51, 52, 53, 54
- linearita transformací mezi inerciálními soustavami 43, 49, 50, 52
- Lorentzovy transformace 28, 49, 52, 55, 56, 57
- prostoročasový interval 50, 51, 52, 53, 54
- rapidita (pseudoúhel) 52, 53, 54, 55, 56, 57
- rychlost inerciální soustavy 52, 53, 54, 55, 56
- úhel mezi žížalami 23, 24, 25, 52, 55, 56
- žížalák Albert 1, 19, 26, 52
Lorentzovy transformace
Vztahy mezi dvěmi inerciálními soustavami souřadnic jsou lineární vztahy, které zachovávají tvar invariantu s2 – jejich nalezení se tak stává jednoduchou algebraickou úlohou.
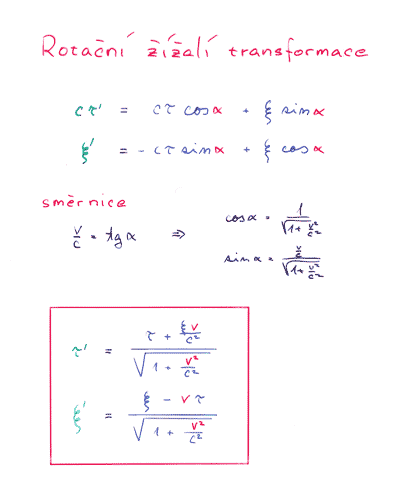
My zde však využijeme analogie s prací žížaláka Alberta. Ten odvodil, že lineární transformace zachovávající vzdálenost nejsou nic jiného než rotační transformace s koeficienty danými goniometrickými funkcemi úhlu otočení. Obdobné transformační vztahy zachovávající relativistický invariant jsou tzv. Lorentzovy transformace, či též boost nebo pseudorotace. Tato tansformace má velice podobný tvar jako rotace, pouze s koeficienty danými místo goniometrcikými funkcemi cos α a sin α úhlu α hypergoniometrickými funkcemi ch β a sh β rapidity (též pseudoúhlu) β.
Nakonec ještě parametrizujeme tyto vztahy rychlostí v (počátku) jedné soustavy vůči soustavě druhé. Ta je s rapiditou svázána vztahem v/c=thβ (jelikož pro x'=0 je v=x/t). Užitím vztahů mezi hypegoniometrickými funkcemi analogickými se vztahy pro goniometrické funkce dostaneme známý tvar Lorentzových transformací mezi dvěmi sadami inerciálních souřadnic.