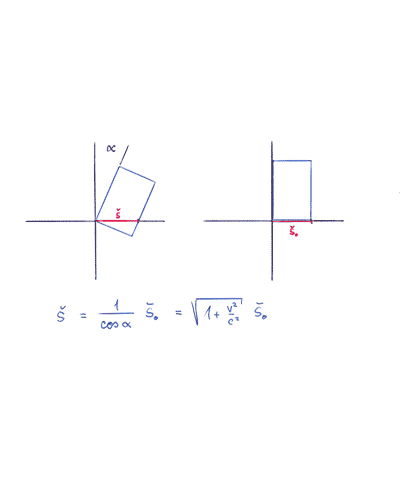- délka a způsob jejího měření 27, 53, 54, 56
- inerciální soustava 27, 28, 32, 42, 47, 49, 50, 52, 53, 54, 55, 56, 57
- invariant Minkowského geometrie 50, 51, 52, 53, 54
- Minkowského geometrie 48, 51, 53, 54, 55, 56, 57
- prostoročasový interval 50, 51, 52, 53, 54
- prostorová vzdálenost, klidová 36, 42, 54
- prostorupodbně položené události 36, 37, 47, 51, 54, 58
- rapidita (pseudoúhel) 52, 53, 54, 55, 56, 57
- rychlost inerciální soustavy 52, 53, 54, 55, 56
- současnost 34, 35, 36, 38, 40, 42, 46, 47, 53, 54, 58
- šířka žížaly 7, 8, 13, 16, 23, 25, 26, 54, 56
- události, prostorupodbně položené 36, 37, 47, 51, 54, 58
- vlastní (klidová) délka 54
- zkracování délek, relativistické, v pohybující se soustavě 54, 56, 57
- zvětšení žížalí šířky 16, 25, 26, 54
Měření délek
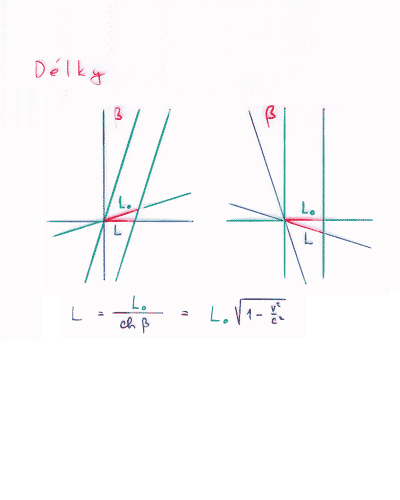
Nyní se podívejme na měření vzdáleností. Pod délkou rakety rozumí pozorovatelka na raketě vzdálenost začátku a konce rakety měřeno ve stejný okamžik ve smyslu současnosti rakety. Této délce se říká vlastní (klidová) délka. V diagramech jsou světočáry začátku a konce rakety vyznačeny zelenými vertikálními čárami, současnost rakety odpovídá zelené horizontální linii. Pozorovatelka na raketě tak naměří délku Lo.
Pozorovatel na Zemi pod délkou rakety chápe také vzdálenost začátku a konce rakety, měřeno však ve stejný okamžik ve smyslu Země. V diagramech je současnost Země vyznačena modrou horizontální čarou, pozorovatel na Zemi naměří délku L.
Vidíme, že pozorovatel na Zemi měří jakýsi horizontální průřez historií rakety; měří jinou veličinu než pozorovatelka na raketě. Opět se tedy nemůžeme divit, že oba pozorovatelé naměří různé hodnoty.
Vztah mezi Lo a L je dán Minkowského trigonometrií. Po vyjádření rapidity β pomocí rychlosti dostaneme známý vzorec pro zkracování délek.
Relativistické měření délek je obdobou žížalího měření šířek. Různě skloněné žížaly měří různé horizontální průřezy a naměří tak různé hodnoty. Pokud jsou žížaly od sebe odkloněny jen nepatrně, rozdíly v šířce jsou zanedbatelné. Stejně tak při běžných rychlostech jsou rozdíly v délkách naměřených různými pozorovateli nepostřehnutelné.
Prostoročasový interval s2 mezi událostmi na začátku a konci rakety současnými vzhledem k raketě je dán výrazem s2 = Lo2. Interval však můžeme vyjádřit v libovolné jiné soustavě, což nám dává obecný vzorec pro vlastní vzdálenost mezi prostorupodobně položenými událostmi
Lo = ( – c2Δt 2 + Δx 2 )1/2 .
Zde Δt a Δx jsou rozdíly souřadnic obou událostí.