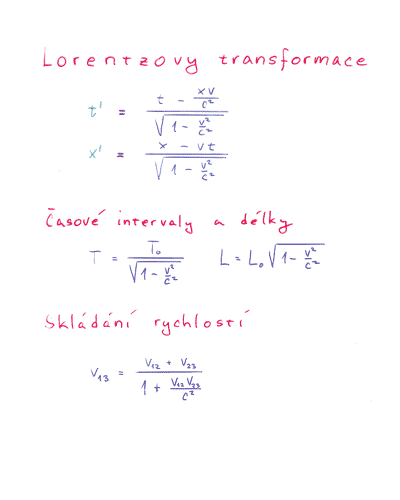- boost 52, 55, 56, 57
- časový úsek (interval) a způsob jeho měření 27, 53, 56
- délka a způsob jejího měření 27, 53, 54, 56
- euklidovská geometrie 20, 22, 24, 42, 48, 51, 55, 56
- inerciální soustava 27, 28, 32, 42, 47, 49, 50, 52, 53, 54, 55, 56, 57
- Lorentzovy transformace 28, 49, 52, 55, 56, 57
- Minkowského geometrie 48, 51, 53, 54, 55, 56, 57
- prodlužování času, relativistické, v pohybující se soustavě 53, 56, 57
- prostoročas 29, 31, 32, 36, 41, 42, 43, 48, 51, 53, 56, 57
- rapidita (pseudoúhel) 52, 53, 54, 55, 56, 57
- rotační žížalí vzorce (transformace) 22, 24, 26, 55, 56
- rychlost inerciální soustavy 52, 53, 54, 55, 56
- skládání rychlostí 27, 28, 55, 56
- skládání směrnic 13, 25, 56
- směrnice (sklon) žížaly 4, 6, 8, 11, 13, 24, 25, 56
- speciální teorie relativity 27, 29, 33, 56, 57, 58
- šířka žížaly 7, 8, 13, 16, 23, 25, 26, 54, 56
- úhel mezi žížalami 23, 24, 25, 52, 55, 56
- výška žížaly 5, 6, 13, 16, 18, 23, 25, 26, 53, 56
- zkracování délek, relativistické, v pohybující se soustavě 54, 56, 57
- žížalí vzorce (transformace), rotační 22, 24, 26, 55, 56
Relativistické vzorce
Shrňme si naše znalosti o prostoročase.
Prostoročas speciální relativity je obdařen Minkowského geometrií podobně jako žížalí svět geometrií euklidovskou. Inerciální soustavy hrají v Minkowského geometrii roli pravoúhlých soustav euklidovské roviny. Transformace od jedné inerciální soustavy k druhé (se společným počátkem) se nazývá boost či obecněji Lorentzova transformce. Tyto transformace jsou obdobou žížalích rotačních transformací.
Rozdílný způsob měření délek a časů vzhledem k různým inerciálním soustavám vede k relativitě těchto veličin. Jedná se o analogii měření šířky a výšky v žížalím světě – tyto veličiny jsou vždy jistým průmětem či průřezem definovaným vůči zvolené soustavě. Při změně soustavy se mění.
Při složením dvou po sobě jdoucích boostů se sčítají jejich rapidity, což vede k složitějšímu vzorci pro skládání rychlostí. Obdobně, v žížalím světě se při postupném otáčení soustav sčítají úhly, což dává složitější vzorec pro skládání směrnic.