prof. Jiří Podolský


![]()
![]()
![]()
Předehra, motivace, nástin obsahu a opakování
Užitečnost alternativních formulací téhož problému ve fyzice. Ilustrace
na teoriích gravitace: Newtonova gravitační síla -> Poissonova rovnice
(pole potenciálu) -> Einsteinova rovnice (pole metriky, obecná teorie relativity).
Teoretická mechanika jakožto vyslovování Newtonových pohybových zákonů
jinými způsoby pro hmotné body, tuhé těleso i kontinuum. Zopakování základních
pojmů mechaniky, Newtonových pohybových zákonů a bude-li čas i mezí platnosti
mechaniky klasické (mechanika relativistická a kvantová).

Pohyb hmotných bodů podrobených vazbám
Síly vtištěné versus reakce podložky. Implicitní popis plochy, normála.
Lagrangeovy rovnice I.druhu (intuitivní zavedení, rozbor a ilustrace na
jednoduchých příkladech). Obecný tvar rovnic pro N hmotných bodů,
v vazeb.
Klasifikace vazeb: jednostranná - oboustranná, holonomní - neholonomní,
skleronomní - rheonomní. Virtuální posunutí a dynamika systému s vazbami:
d'Alembertův princip. Důsledky principu: Newtonovy rovnice pro pohyb bez vazeb,
hledání rovnováhy pomocí principu virtuální práce, ekvivalence s Lagrangeovými rovnicemi
I.druhu.
Lagrangeovy rovnice II.druhu
Zobecněné souřadnice aneb nepoužívejme jen (x,y,z). Occamova břitva
aneb nepoužívejme více souřadnic, než kolik je nezbytně nutno. Konfigurační
prostor: Zénónův paradox šípu a nezávislost zobecněných rychlostí na zobecněných souřadnicích.
Odvození Lagrangeových rovnic II.druhu. Lagrangeova funkce L :
případ bez potenciálu, s potenciálem, se zobecněným potenciálem
(pohyb částice v elektromagnetickém poli). Ilustrace jak elegantně dospět
k pohybovým rovnicím na příkladě cykloidálního kyvadla.

Pravidla, metody a triky Lagrangeova formalismu
Kuchařka pro sestavení pohybových rovnic (vhodná volba zobecněných
souřadnic, vyjádření T a V v těchto souřadnicích, sestavení
L
,
příslušné derivace, jejich dosazení do Lagrangeových rovnic II.druhu).
Ilustrace: pohyb částice v poli centrální síly. Metody a triky integrace
pohybových rovnic: hledání přibližného řešení pomocí linearizace (matematické
kyvadlo), hledání integrálů pohybu (cyklické souřadnice -> zachování zobecněných
hybností, explicitní nezávislost L na čase -> zachování zobecněné
energie). Ilustrace: Binetův vzorec pro pohyb v centrálním poli.
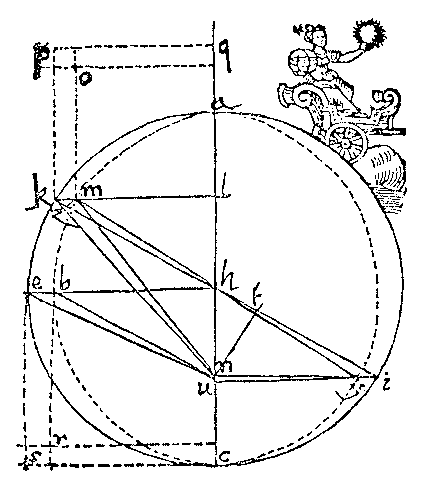
Pohyb planet a další aplikace
Keplerova úloha neboli obíhání planet v gravitačním poli Slunce. Odvození
Keplerových zákonů. Metoda efektivního potenciálu. Srovnání klasické a relativistické mechaniky:
pohyb kolem Slunce versus pohyb kolem černé díry, stáčení perihélia. Převedení
problému dvou těles na pohyb částice s redukovanou hmotností v poli centrální
síly. Problém 3 těles a nebeská mechanika, několik slov o chaosu.
Rozptyl částic, efektivní průřez a Rutherfordův vztah.
Hamiltonův variační princip
Základy variačního počtu (motivace a vysvětlení pojmu extremála: Fermatův
princip, brachystochrona, geodetiky v obecné teorii relativity). Odvození
podmínky pro extremálu: Eulerovy-Lagrangeovy rovnice. Definice akce a Hamiltonův variační princip
mechaniky. Jeho hlavní důsledky: Lagrangeovy rovnice II.druhu i I. druhu.
Symetrie a zákony zachování (teorém Emmy Noetherové pro invariantní L
).
Zmínka o kalibračních transformacích a polích. Náznak zobecnění variačního
přístupu pro pole klasické i kvantové.

Hamiltonovy kanonické rovnice a Poissonovy závorky
Zobecněná hybnost neboli kanonicky sdružený impuls. Zavedení fázového
prostoru s ukázkami různých pohybů (oscilátor, tlumení, chaos). Hamiltonova
funkce. Odvození Hamiltonových kanonických rovnic z Hamiltonova principu
i z rovnic Lagrangeových. Ilustrace kanonických rovnic (harmonický oscilátor,
částice v elektromagnetickém poli). Význam Hamiltonova formalismu pro kvantovou
teorii (Schrödingerova rovnice, Feynmanovy diagramy jakožto rozvoj interakčního
hamiltoniánu) a statistickou fyziku (partiční funkce). Definice, základní
vlastnosti a algebra Poissonových závorek. Analogie s komutátory v kvantové
mechanice.

Kanonické transformace a Hamiltonova-Jacobiho teorie
Kanonické transformace, generující funkce a podmínky kanoničnosti (přehled
základních algoritmů, příklad). Analogie s termodynamickými potenciály.
Odvození Hamiltonovy-Jacobiho rovnice jakožto důsledku vhodné kanonické
transformace, algoritmus jejího řešení, metoda separace proměnných a příklad
(volný pád). Aplikace ve fyzice: optika (vlnoplocha -> paprsek), kvantová
mechanika (kvaziklasické přiblížení: Schrödingerova rovnice -> Hamiltonova-Jacobiho
rovnice), Feynmanova formulace kvantové teorie pomocí dráhových integrálů.

Mechanika tuhého tělesa
Opakování vektorů a tenzorů v Euklidovském prostoru. Grupa konečných
rotací a algebra infinitesimálních rotací. Jejich reprezentace pomocí antisymetrických
matic a zavedení vektoru úhlové rychlosti jakožto duálu k nim. Otáčení
tělesa kolem pevné osy, tenzor setrvačnosti. Vlastní čísla a vektory
včetně interpretace elipsoidu setrvačnosti. Kinetická energie rotačního
pohybu. Rozklad pohybu na translaci a rotaci (Chaslesova věta). Důsledek
pro kinetickou energii (Koenigova věta). Drobná perlička: jednoduché odvození
pohybových rovnic v neinerciálním systému z Lagrangeovy funkce.
Eulerovy rovnice a setrvačníky
Eulerovy úhly a Eulerovy kinematické rovnice. Lagrangeova funkce pro
tuhé těleso a odvození Eulerových dynamických rovnic. Ukázkové příklady:
analýza pohybu symetrického bezsilového setrvačníku.

Teorie kontinua
Přechod od soustavy hmotných bodů ke spojitému prostředí. Ilustrace:
hustota Lagrangeovy funkce pro podélné kmity soustavy oscilátorů a příčné
kmity struny. Odvození Eulerových-Lagrangeových pohybových rovnic pro spojité
prostředí z Hamiltonova principu. Vlnová rovnice a základní metody jejího
řešení: a) d'Alembertova metoda, b) separace proměnných (vlastní frekvence,
okrajové a počáteční podmínky, Fourierova analýza). Perspektivy: klasická
pole a jejich kvantování. Dva možné popisy pohybu kontinua: Lagrange versus
Euler. Vektor posunutí a pole rychlosti.
Základní veličiny a rovnice pro popis kontinua
Připomenutí tenzoru malých deformací a tenzoru napětí.
Pohybová rovnice obecného kontinua
a rovnice kontinuity, podmínky rovnováhy. Reologická klasifikace látek
(od tuhé látky po ideální tekutinu). Zobecněný Hookův zákon pro izotropní
těleso s interpretací příslušných koeficientů.
Nejzajímavější důsledky rovnic kontinua
Pohybová rovnice izotropního prostředí. Eulerova pohybová rovnice
ideální tekutiny a vlny v ní, odvození rychlosti
zvuku. Bernoulliova rovnice jakožto 1.integrál. d'Alembertův hydrodynamické
paradoxon pro nevířivou a nestlačitelnou ideální tekutinu. Navierova-Stokesova
pohybová rovnice pro vazkou tekutinu. Ilustrace: proudění dlouhou trubicí
(odvození parabolického rychlostního profilu a Poiseuillova-Hagenova zákona).
Krátce o laminárním proudění versus turbulenci a Reynoldsově čísle.
![]()
![]()
![]()
© J. Podolský, 30. září 2024