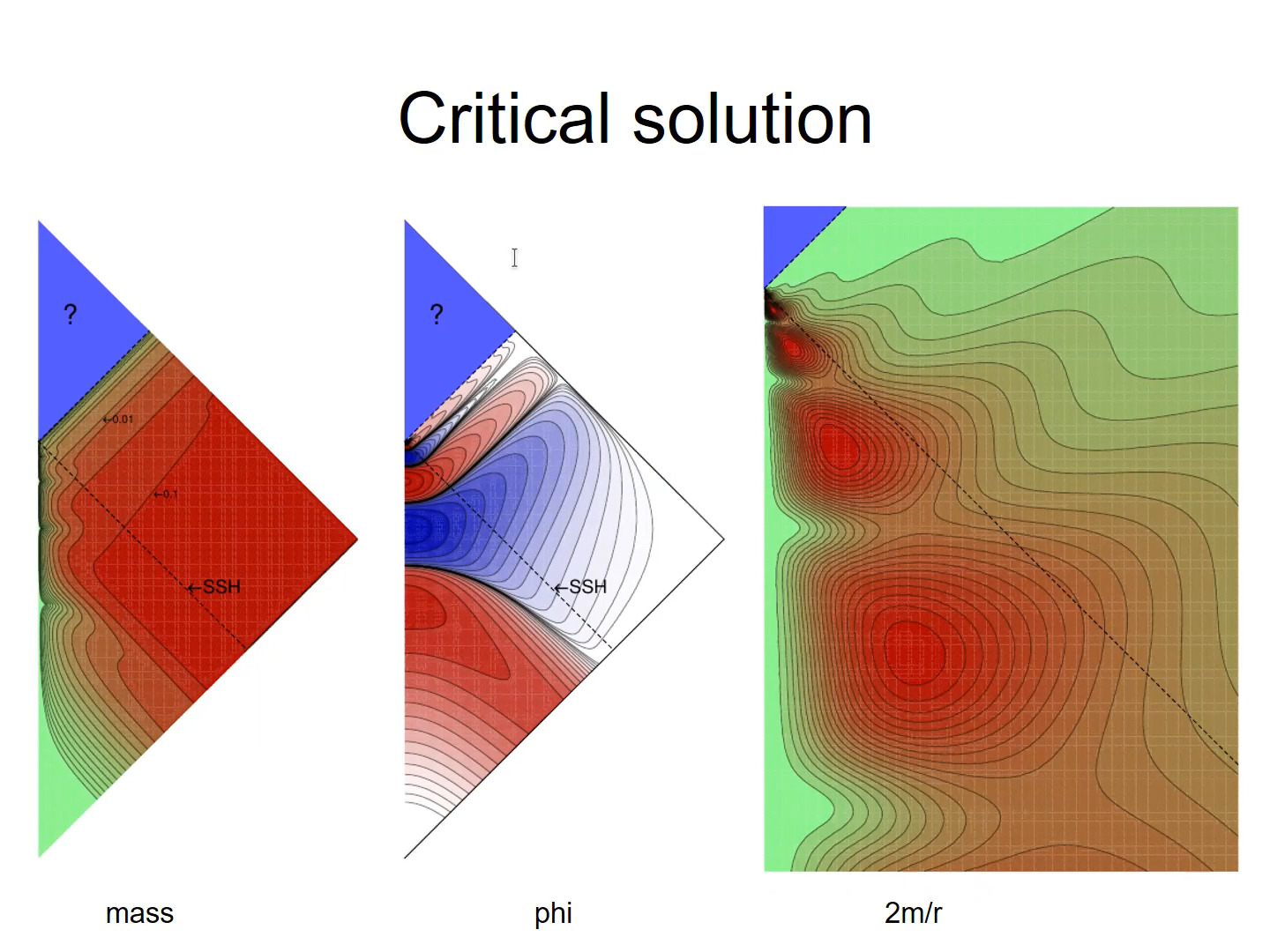
We consider several families of asymptotically flat initial data which, similar to the well-known Choptuik's discovery, can be fine-tuned between dispersal into empty space and collapse into a black hole. We discuss the applied methods and then we show that near-critical spacetimes exhibit behavior similar to scalar-field collapse: For different families of initial data, we observe universal "echoes" in the form of irregularly repeating, approximate, scaled copies of the same piece of spacetime.
Záznam:
It is shown that the Ablowitz-Kaup-Newell-Segur (AKNS) integrable hierarchy can be obtained as the dynamical equations of three-dimensional General Relativity with a negative cosmological constant. This geometrization of AKNS system is possible through the construction of novel boundary conditions for the gravitational field. These are invariant under an asymptotic symmetry group characterized by an infinite set of AKNS commuting conserved charges. Gravitational configurations are studied by means of SL(2,R) conjugacy classes. Conical singularities and black hole solutions are included in the boundary conditions.
Záznam:

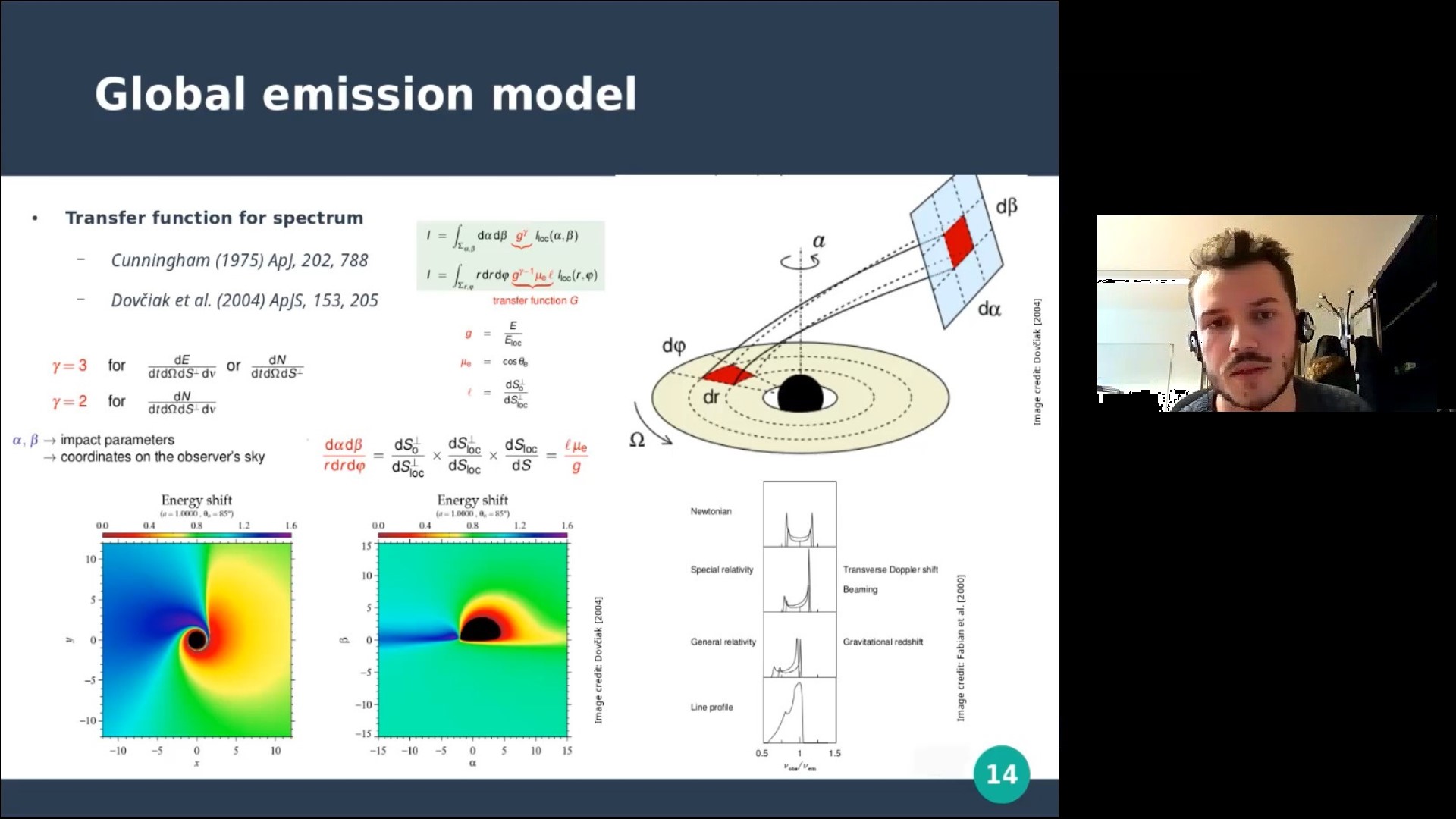
We present the theoretical spectrum and polarisation properties of X-ray emission from accretion discs in active galactic nuclei (AGN) including relativistic effects. The reflected radiation from an accretion disc illuminated by a hot corona above is computed using the Monte Carlo radiative transfer code STOKES. The structure of the disc, modelled as a constant density slab, has been computed with the code for optically thick and hot photo-ionized media TITAN. The resulting simulated spectra locally emitted by the accretion disc in 0.1–100 keV energy band are compared to the results obtained by various, published radiative transfer codes. In addition to these, the STOKES code also provides the polarisation degree and polarisation angle of the outcoming radiation that depend on the geometry of scattering and other key parameters such as the ionisation of the disc. Further, we use the relativistic code KYNSTOKES to account for relativistic effects on radiation near a black hole and to compute the total disc emission as would be detected by a distant observer. In this way it is then possible to predict X-ray spectral and polarisation properties of an accretion disc in AGN and their dependence on various parameters of the system (spin of the black hole, geometry of the corona, ionization of the accretion disc, observer inclination). This is fundamental for the interpretation of AGN spectra and polarisation obtained by the upcoming X-ray polarimetric missions, such as NASA IXPE mission or Chinese-lead eXTP mission.
Záznam:
We will briefly review the general parametrization of the axially symmetric black hole spacetime, which is similar in spirit to the parametrized post-Newtonian approximation, but valid in the whole space outside the event horizon, including the near horizon region. Then, we consider the Blandford-Znajek process of electromagnetic extraction of energy from a general axially symmetric asymptotically flat slowly rotating black hole given in the parametrized form. Using the general parametrization of the black-hole spacetime we construct formulas for the flux of the magnetic field and the rate of energy extraction, which are valid not only for the Kerr spacetime, but also for its arbitrary axially symmetric deformations. We show that in the dominant order these quantities depend only on a single deformation parameter, which relates the spin frequency of a black hole with its rotation parameter.
Záznam:
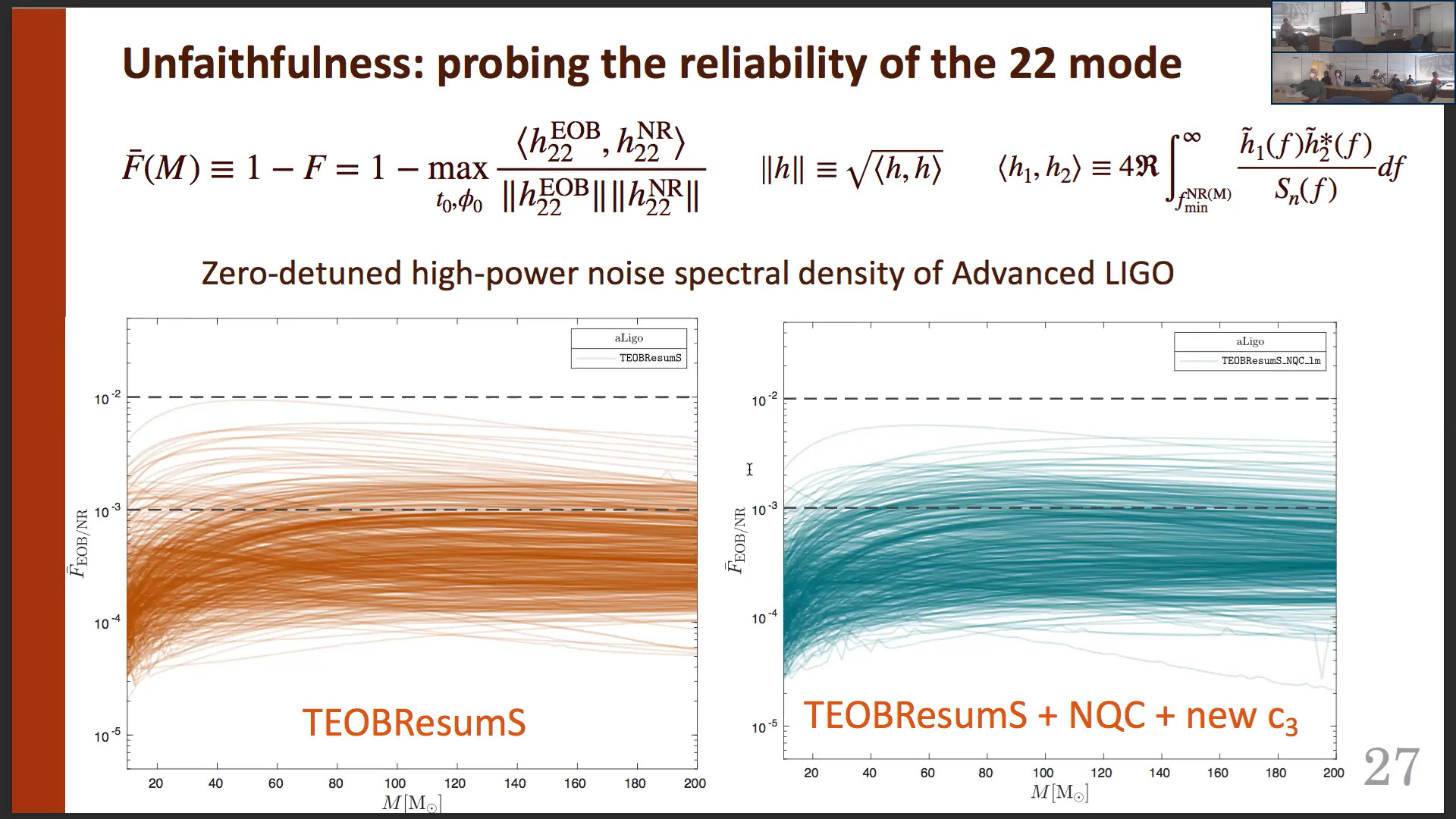
The coalescence of a compact binary system generates gravitational waves. In order to detect the signal, fast and accurate waveform templates are needed. Though numerical relativity simulations provide exact results, they come at a high computational cost and cannot cover the whole parameter space. Semi-analytical models allow instead a fast waveform generation and are thus of fundamental relevance from an experimental point of view. Different families of these models come from the Effective-One-Body (EOB) formalism, which reformulates the two-body problem in GR as the motion of a particle with the reduced mass of the system in an effective metric. We will briefly review the building blocks of the EOB approach and then give details about TEOBResumS, a state-of-the-art EOB model that yields complete waveforms for nonprecessing coalescing black hole binaries on quasi-circular orbits.
Záznam:
Accretion disks of massive central objects are well established in theory and observation as efficient engines of potential-to-radiant energy conversion in our universe. Concretely in the case of a black hole as the massive central object, accretion disk serves as a transmitter for an otherwise not (meaningfully) radiating object, signalling her existence and parameters (due to inescapably relativistic nature of the disk) for an interested distant observer. Theories of accretion disks exist for a variety of disk classes; we are interested in thin, optically thick disks with an inner edge; "thin disks" for short. The eminent theory in this class being the relativistic Novikov-Thorne theory, operating on a fixed Kerr spacetime background and establishing the thin disk composed of magnetized ionized gas, with viscosity prescribed phenomenologically, stemming from turbulences. The spectrum of incoming radiation carries a signature of black hole & accretion disk parameters, most notably the black hole mass, spin and the disk's accretion rate. Fitting a spectrum predicted by the Novikov-Thorne theory to the observed spectrum ought to determine the parameters, for each observation in many. However, after doing so, a clear discrepancy appeared - when the spin and accretion rate extracted from multiple observation were plotted against each other, a decay of spin as depending on accretion rate appeared, when it should be constant. We sought to explain this discrepancy by modifying the standing Novikov-Thorne theory, by assuming that not all energy viscously generated is immediately radiated away, but instead a portion of it is transferred inward, an advective process mediated by magnetic field.
Záznam (bohužel velmi nekvalitní - omlouvám se):

Prezentace:

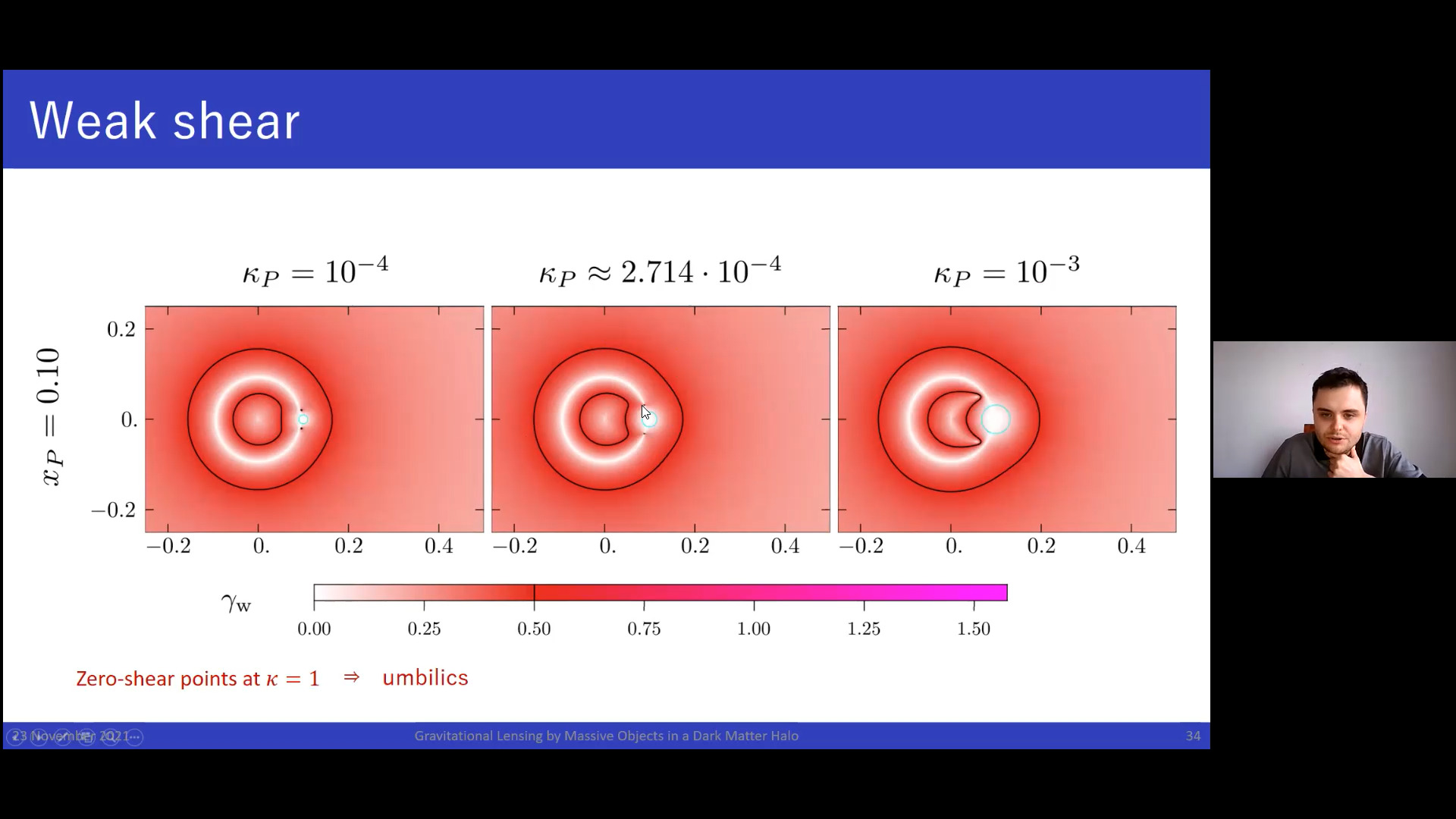
Among many other things, gravitational lensing can be used to survey the matter content of galaxy clusters. However, recent studies showed major discrepancy in halo substructure lensing efficiency between observed clusters and those from cosmological simulations. The role of halo substructures in gravitational lensing thus asks for deeper investigation. We take a bottom-up approach, starting with detailed examination of the simplest model composed of dark matter halo with Navarro—Frenk—White profile and single perturbing point mass. We study critical curves and caustics, discovering unexpected richness of caustic transitions. Next, we analyze geometry of images including implications for weak-lensing quantities. Then we proceed further to more realistic models of the galaxy cluster with multiple point mass perturbations and eventually with truncated elliptical NFW subhalos.
Záznam:
Série šesti krátkých seminářů kandidátů na pozici postdoca na ÚTF.
- 13:15 Matthew Terje Aadne
- (University of Stavanger)
- 13:45 Arpita Mitra
- (Indian Institute of Science Education & Research Bhopal)
- 14:15 Carlos Peón-Nieto
- (University of Salamanca)
- 15:00 Jorge G. Valcarcel
- (University of Tartu)
- 15:30 Andriú Conroy
- (Dublin City University)
- 16:00 Luca Ciambelli
- (Université Libre de Bruxelles)
Příspěvky budou předneseny přes Zoom:
https://cesnet.zoom.us/j/92851596816?pwd=YnUwZTVYYjA5enBLTk9RcjFpUEJXQT09.
Workshop bude živě promítán v přednáškové místnosti ÚTF.
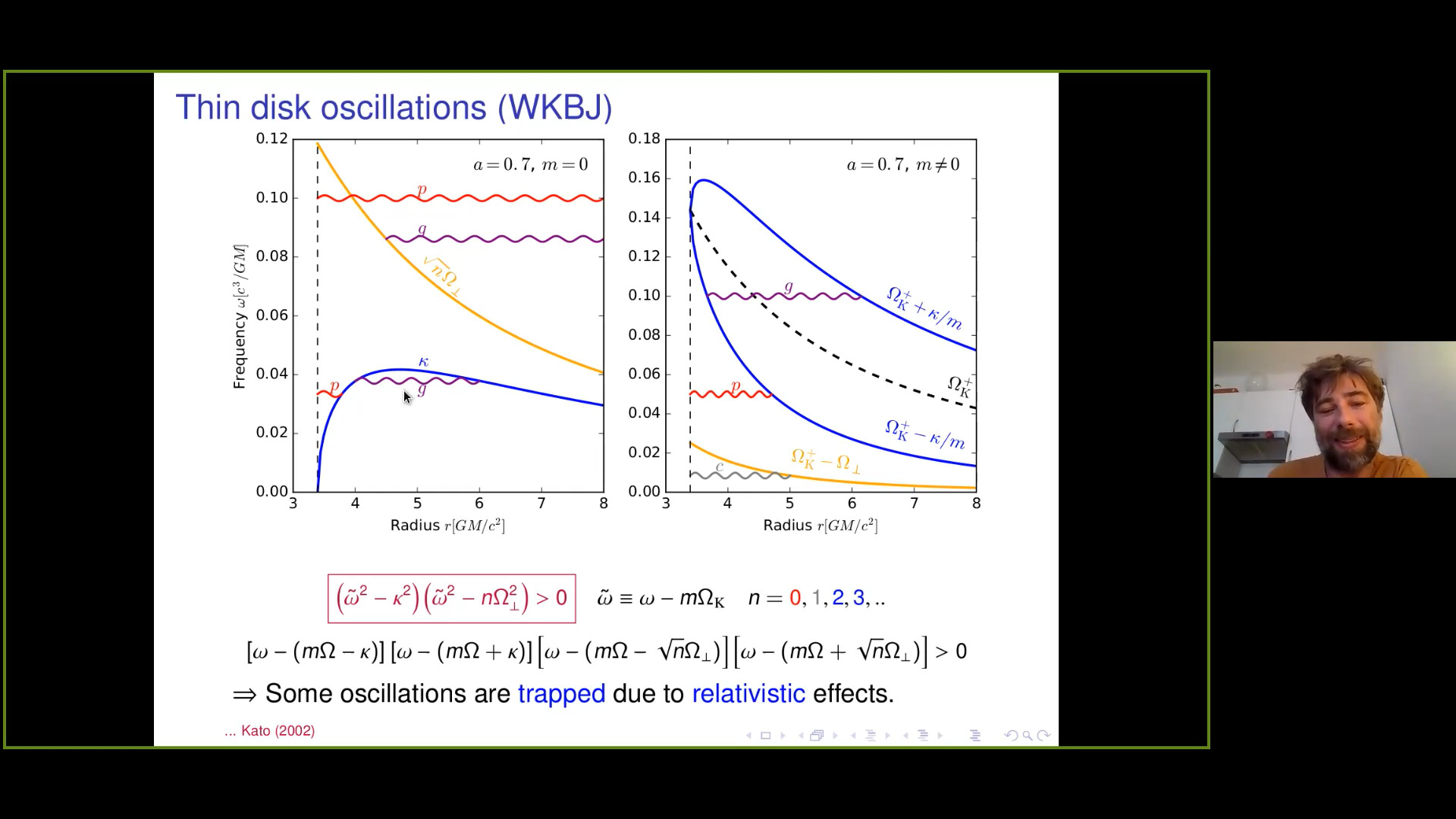
Due to general relativistic effects, accretion disks surrounding black holes can host self-trapped oscillations close to their inner edges. This talk is devoted to their nonlinear evolution. We will discuss change of the trapping region and oscillation frequency of the g-modes when the amplitude of the oscillations is significant. When non-linearities in the hydrodynamic equations are taken into account, the g-modes are coupled to other oscillation modes. We will also discuss their impact on the original oscillations.
Záznam:
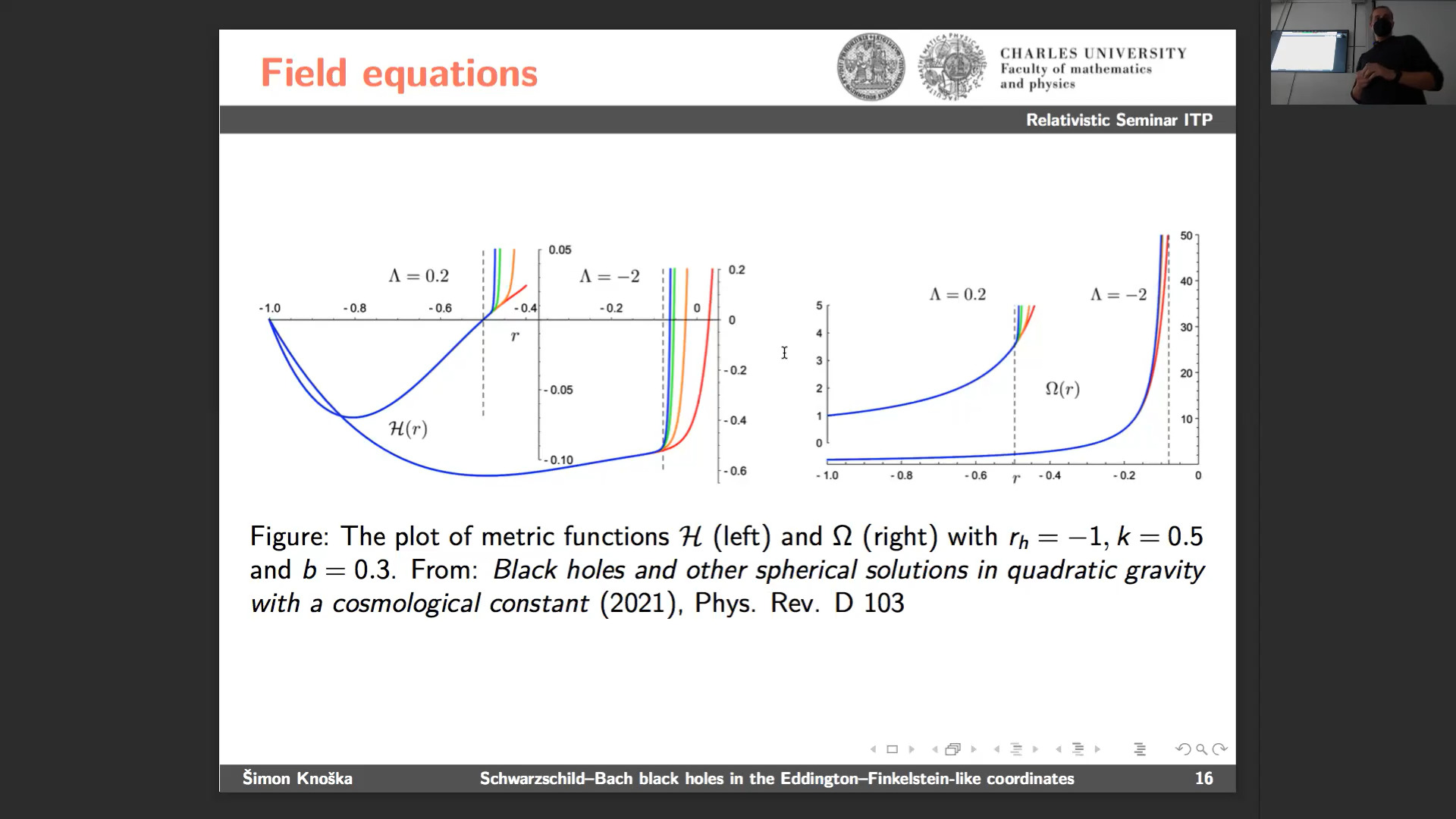
We analyse spherically symmetric solutions in the quadratic gravity which represents the GR natural modification including quadratic corrections in its action. We extend previous works employing the Eddington–Finkelstein-like coordinates. This allows to find the explicit solution in the form of power series, analogously to the previous approach which used the conformal-to-Kundt metric form, however, our results provide more direct transition to the classic Schwarzschild-like coordinates and more naturally elucidate physical and geometrical properties of the resulting solution such as basic aspects of geodesic motion, the quadratic gravity mass contribution, or presence of the cosmological horizon.
Záznam:
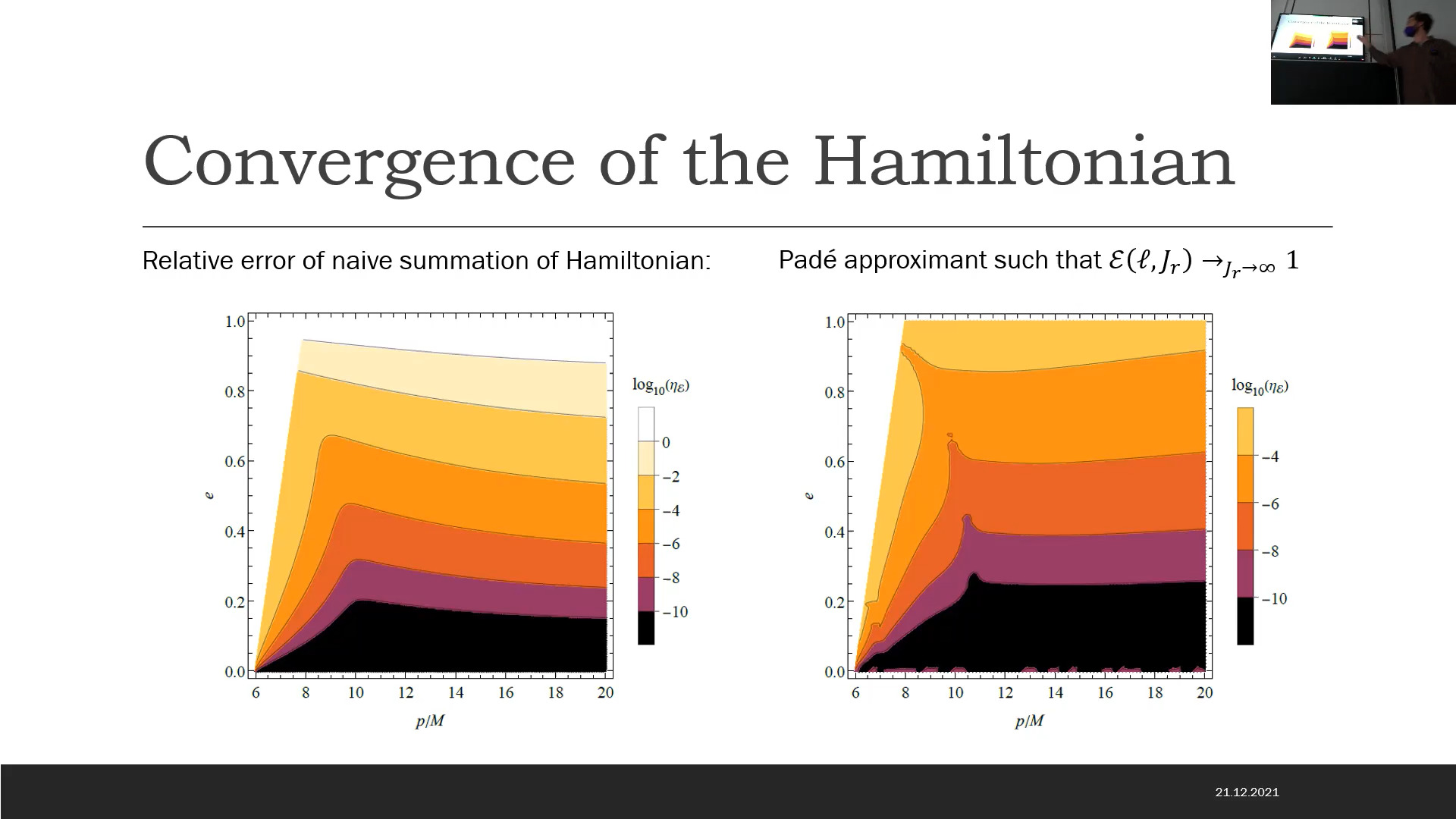
Imagine there is a way to solve any set of equations of motion by transforming them into trivial ones. That is what action-angle (AA) coordinates do for Hamiltonian mechanics. Of course, the issue is that by doing so, you just move the problem from solving the equations of motion to finding the transformation. Nevertheless, even a perturbative transformation to AA coordinates represents an efficient and systematic way of storing and representing the solution. Additionally, AA coordinates are an extremely useful starting point for perturbation theory of the original equations of motion. In this talk I show how transformations to and from action-angle coordinates can be found for black-hole geodesics and how that simplifies gravitational-wave inspirals both in the extreme and comparable mass ratio regimes.
Záznam:
We discuss a prescription to compute the gravitational multipole moments of compact objects for asymptotically de Sitter spacetimes. Our prescription builds upon a recent definition of the gravitational multipole moments in terms of Noether charges associated to specific vector fields, within the residual harmonic gauge, dubbed multipole symmetries. We derive the multipole symmetries for spacetimes which are asymptotically de Sitter. We apply our prescription to the Kerr-de Sitter black hole and compute its multipole structure. Our result recovers the Geroch-Hansen moments of the Kerr black hole in the limit of vanishing cosmological constant.
Záznam:

Many familiar metrics of general relativity have been achieved by integrating the Einstein equations for a particular source stress-energy tensor. In other cases, physical considerations lead to a motivation for studying metrics of a particular form; here, then, the question is to derive the stress-energy tensor from a given metric. While mathematically simpler—as differentiation is simpler than integration—this opens a long list of questions which stress-energy tensors should be considered physical. An early heuristic for such an evaluation were so-called energy conditions. In particular for many science-fiction-inspired metrics, attempts to produce these without violating the (point-wise) energy conditions has become a staple of the search for new reverse-engineered solutions. Here, I will present a quite general proof for the violation of the null energy condition in "warp field" space-times, and describe a new engineered solution, "tractor beams". These can serve as a cautionary tale of what to expect of energy condition violations, and I will try to ask—and partially answer: "Quo vadis, energy conditions?"
Záznam:
I will introduce and discuss the concepts of bulk flows and peculiar velocities, the importance of which has progressively been shown to be more significant in modern cosmology. Alongside this, I will also discuss recent theoretical developments of a new way of expanding luminosity distances in terms of null geodesics, allowing us to obtain null analogues of the well-known expansion and deceleration parameters. I will wrap up by connecting both topics and analyzing the effect of peculiar velocities in the null deceleration parameter, as well as open a discussion on the impacts of such results on the existence of dark energy.
Záznam:

The Lense-Thirring spacetime describes a 4-dimensional slowly rotating approximate solution of vacuum Einstein equations valid to a linear order in rotation parameter. It is fully characterized by a single metric function of the corresponding static (Schwarzschild) solution. We shall discuss a generalization of the Lense-Thirring spacetimes to the case that is not necessarily fully characterized by a single (static) metric function. This generalization lets us study slowly rotating spacetimes in various higher curvature gravities as well as in the presence of non-trivial matter such as non-linear electrodynamics. In particular, we construct slowly multiply-spinning solutions in Lovelock gravity and notably show that in four dimensions Einstein gravity is the only non-trivial theory amongst all up to quartic curvature gravities that admits a Lense-Thirring solution characterized by a single metric function. The "magic square" upgraded version of our ansatz can be cast in the Painlevé-Gullstrand form (and thence is manifestly regular on the horizon) and admits a tower of exact rank-2 and higher rank Killing tensors that rapidly grows with the number of dimensions.
Záznam:
