Problem of light rays propagating around compact relativistic objects (e.g. a black hole) is usually solved with a vacuum background. However, in real astrophysical applications a medium (plasma) surrounding a vicinity of the black hole has to be considered. Studies describing ray trajectories around relativistic objects in plasma typically focus on particular examples and discuss concrete spacetime and plasma effects. This problem can be effectively solved as the separation of the Hamilton-Jacobi equation. To be able to find a solution of such system, a Carter constant has to exist. In our work, we state general conditions for both the axially symmetric stationary metric and plasma density which guarantee that the Carter constant exists. General expressions for a photon region and black hole shadow for light rays penetrating around an axially symmetric stationary object in plasma are further derived. Moreover, the obtained general relations are applied to find the boundary of photon region and shadow for particular examples, such as Kerr metric or Melvin metric.
Recording:

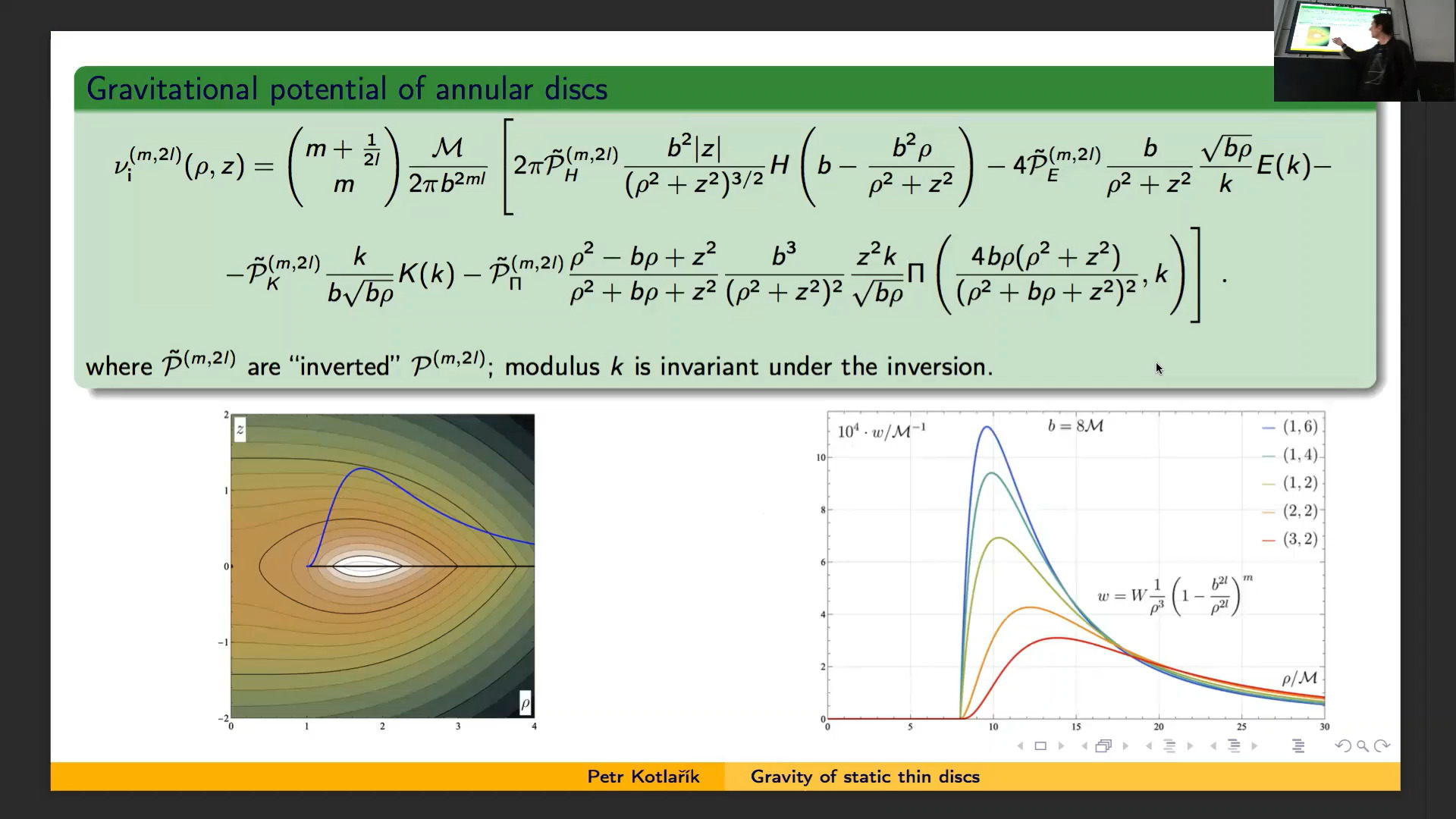
Thin discs are important structures in astrophysics. Whether treated in Newton's theory or in general relativity, in the static and axially symmetric case they generate potential determined by the Laplace equation. Though clear in principle, its solution is only known explicitly for several surface-density profiles. We show how to derive close-form potentials for the densities composed of powers of the radius. The method, due to Conway (2000), rests on the Laplace transform of products of Bessel functions. Finite as well as infinite discs will be included, possibly empty at their centre (i.e. annular).
Recording:
Cauchy problem in all dimensions for Lambda positive vacuum spacetimes: the Friedrich conformal field equations in four spacetime dimensions and the Fefferman-Graham formalism in higher dimensions. We employ the initial data to asymptotically characterize Kerr-de Sitter and related spacetimes.
Recording:

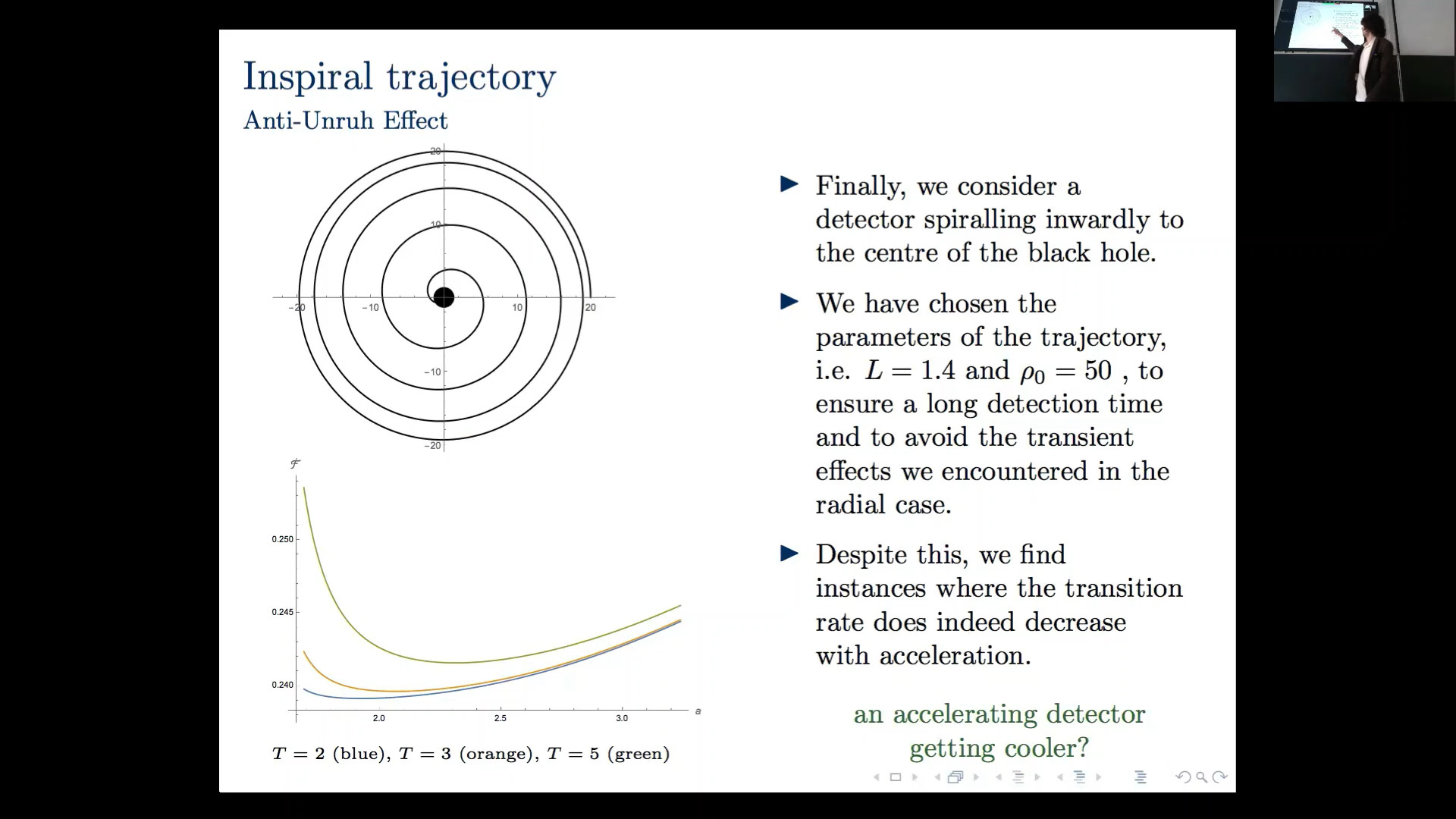
There is no well-defined notion of a particle in quantum field theory in curved spacetime due to the lack of global symmetries. The standard procedure in quantum field theory is to treat fields rather than particles as the fundamental object of interest. Nevertheless, in a seminal 1976 paper by W. G. Unruh, an operational meaning was given to the particle concept by examining the absorption and emission of field quanta by a two-level atom. This is the so-called Unruh-DeWitt detector and, in this operational sense, we say a particle is what a particle detector detects! Computing the response of an Unruh-DeWitt detector in black hole spacetimes is technically challenging – a fact which has largely limited the literature to stationary detectors. In this talk, we consider the response of an Unruh-DeWitt detector near an extremal charged black hole, modelling the near-horizon region of this extremal spacetime by the Bertotti-Robinson spacetime. The advantage of employing the Bertotti-Robinson limit is that the two-point functions for a massless scalar field are obtainable in closed form for a number of quantum states of interest, allowing us to explore the full gamut of the parameter space for a broader range of stationary and non-stationary trajectories. Particular attention will be paid to the thermalization of the detector, the anti-Unruh effect, and the anti-Hawking effect. If time allows, I will then move on to discussing some unpublished results on the open question of how to define surface gravity and temperature in dynamical spacetimes by shifting focus to a detector in a cosmological spacetime with an evolving horizon.
Recording:
We investigate axisymmetric extremal isolated horizons (EIHs). They are described by an induced metric characterized by a single function. This function is subject to particular constraints following from Ricci identities in the Einstein-Maxwell theory. At first, we restrict our attention to asymptotically flat spacetimes. In the extremal case the solution is unique and depends on 5 independent parameters with direct geometrical or physical interpretation. The solution is possible to identify with extremal horizons in exact electrovacuum Plebański-Demiański spacetimes, that are all (double aligned) black holes of algebraic type D without a cosmological constant. Several interesting subclasses include accelerating extremely charged Reissner-Nordström black hole (C-metric) or extremal accelerating Kerr-Newman. As a natural extension, I will generalize the previous results to asymptotically (anti-) de Sitter spacetimes with non-zero cosmological constant and identify the EIHs geometry with the corresponding horizon geometry of a black hole in a special case of the famous Kerr-Newman-NUT-(A)dS metric.
Recording:

The Einstein-Maxwell equations for a charged rotating black hole in 5 dimensions with two equal-magnitude angular momenta has been reduced to a system of non-linear ODEs and studied numerically by Kuntz et al. We study some geometric aspects of these solutions, confirming that they have regular horizon and null infinity. In addition, we rule out the possibility that the Weyl tensor of these spacetimes has special algebraic type in the bulk, while verifying the "geometric horizon" conjecture by showing that the Weyl tensor reduces to Type II on the horizon and to Type D on the bifurcation sphere.
Recording:

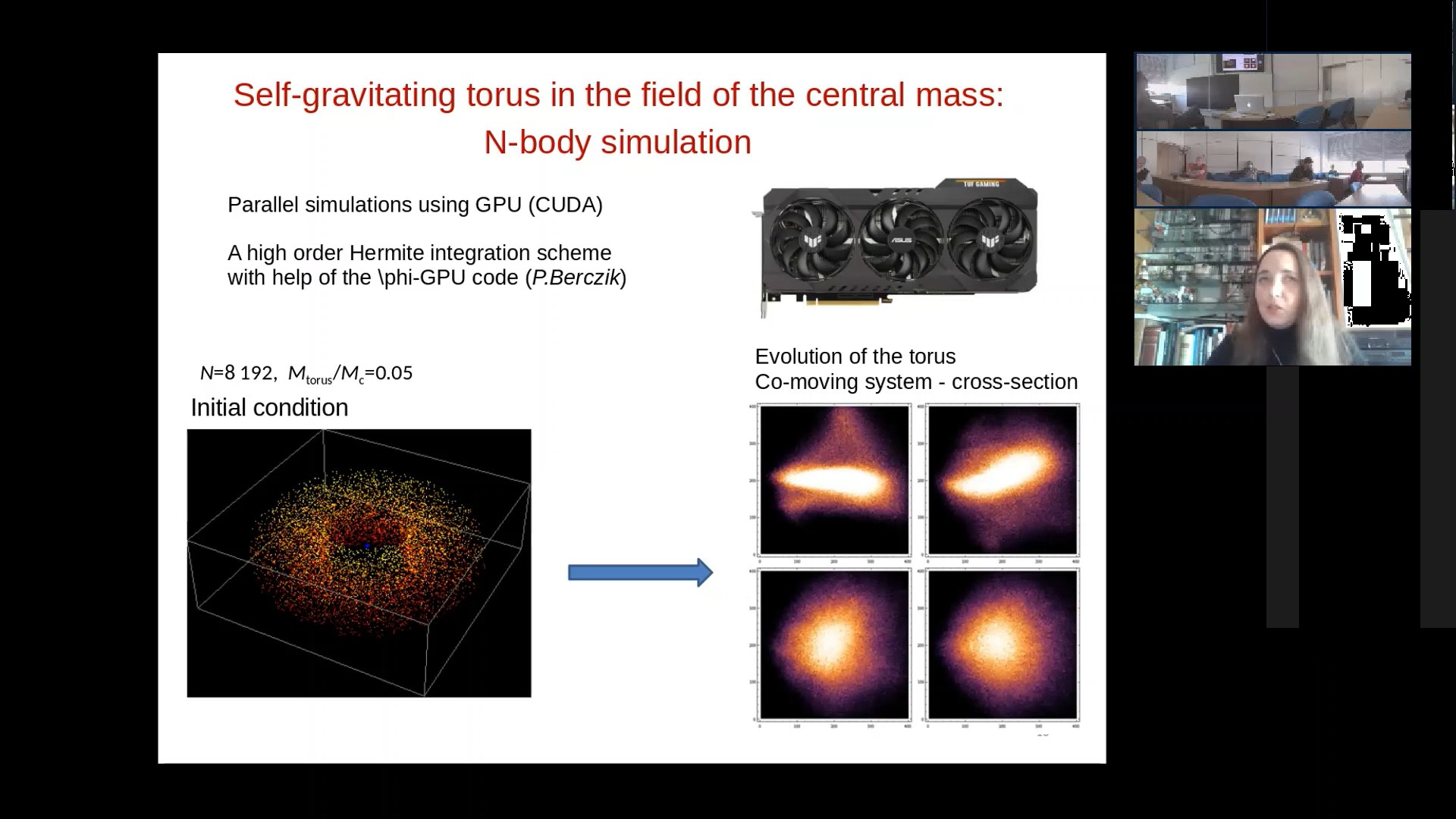
The recent paradigm of AGNs is to explain the differences between type I and II by the different orientation of an optically thick torus relative to the observer. The dynamics of the dusty clouds in such a torus was unclear due to the relative small scale of these objects. The unprecedented resolution of ALMA has recently allowed us to improve significantly the information about dynamics of clouds in the obscuring tori for some AGNs. On this ground, we present our N-body simulations of the toroidal structure of clouds moving around a supermassive black hole (SMBH). We also apply ray-tracing algorithm to take into account effects of obscuration of the central engine by the clouds. As the final result, we obtain the velocity and temperature maps which allow us to interpret the VLTI and ALMA observations. We also estimate the SMBH masses in the nearest Sy2 galaxies and provide a new explanation of the counter-rotation of the torus in NGC 1068.
Recording:
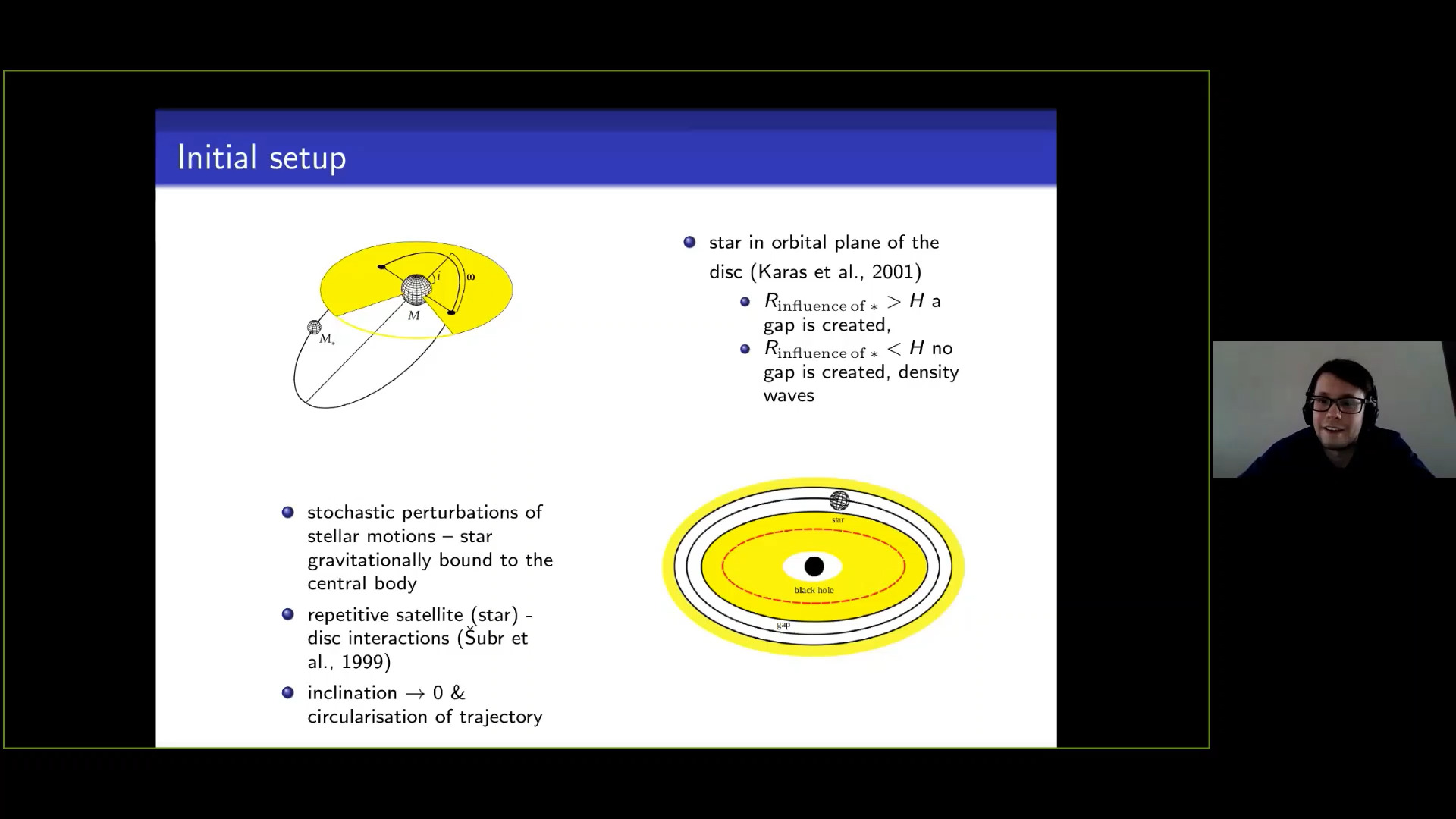
Both spectral energy distribution of the continuum and the spectral lines offer a way to measure and model parameters of the inner and outer region of the black hole accretion disc. We introduce a perturbative term in the orbital plane of the accretion disc and assume different scenarios pointing towards a gappy accretion disc setup. Studying the radiative effects of the perturber, we discuss the application of the methods used to constrain the parameters of the system.
Recording:
By employing the methods of canonical perturbation theory we can find an approximate analytical solution to a Hamiltonian system. We applied this approach to the geodesic equation in the spacetime describing a black hole superposed with a ring-like source. The solutions to the geodesic equation are then used to compute gravitational wave fluxes using the quadrupole formalism. This allows us to compute the extreme mass ratio inspiral (EMRI) in our spacetime by adiabatically evolving the constants of motion which parametrize the analytical solution of the geodesic equation.
Recording:

We present the complete family of higher-dimensional Robinson-Trautman (RT) spacetimes sourced by (aligned) conformally invariant non-linear electrodynamics with an arbitrary cosmological constant. We also briefly compare the obtained results with the known ones in the case of RT spacetimes with linear Maxwell field in higher dimensions. Subsequently, some properties of a static subclass are also investigated. It contains dyonic black holes with various horizon geometries and different asymptotics. Finally, we discuss the special case of stealth solutions.
Recording:

We present a "holographic" reconstruction of bulk spacetime geometry using correlation functions of a massless field living at the "future boundary" of the spacetime, namely future null infinity I+. It is holographic in the sense that there exists a one-to-one correspondence between correlation functions of a massless field in four-dimensional spacetime M and those of another massless field living in three-dimensional null boundary I+. The idea is to first reconstruct the bulk metric by "inverting" the bulk correlation functions and re-express the latter in terms of boundary correlators via the correspondence. This effectively allows asymptotic observers close to I+ to reconstruct the deep interior of the spacetime using only correlation functions localized near I+.
Recording:

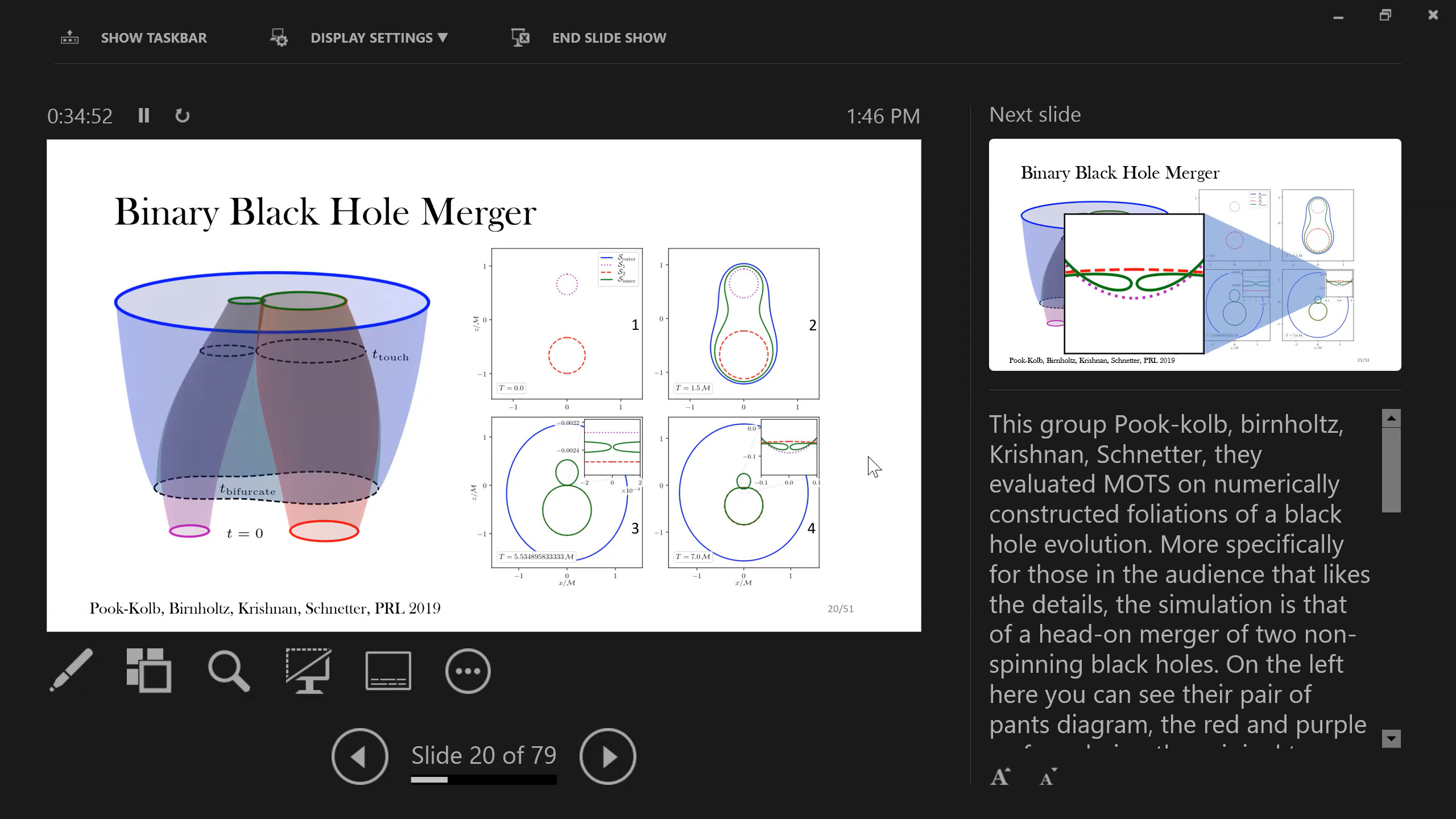
The advent of gravitational wave detectors had facilitated a constant stream of black hole merger observations. Despite this, black hole mergers are not fully understood. The details of the two apparent horizons becoming one is unclear due to the non-linear nature of the merger process. Recent numerical work has shown that there is an appearance of self-intersecting marginally outer-trapped surfaces (MOTS) during the black hole merger [Pook-Kolb et. al. arXiv:1903.05626]. Following papers have found similarly behaving MOTS in a simpler and static scenario, that of a Schwarzschild black hole, where a seemingly infinite number of self-intersecting MOTS were found [Booth et. al., arXiv:2005.05350]. This talk introduces new phenomena that occur in the presence of an inner horizon. For Reissner-Nordstrom and Gauss-Bonnet black holes, we find that the maximum number of self-intersections becomes finite with the MOTS parameter space deeply dependent on the interior structure of the black hole and in particular the stability of the inner horizon [Hennigar et. al., arXiv:2111.09373].
Recording:
Recording: