Funkce
Při psaní programů je pohodlné a správné konkrétní výpočty izolovat do k tomu určených funkcí:
Pokud takový výpočet potřebujeme v programu na více místech, ušetříme si práci
Výpočet izolovaný do podoby funkce lze snáze testovat
Rozdělení na kódu menší části (kdysi se říkalo podprogramy) nám umožňuje snáze rozmýšlet o jeho fungování
Hned na první lekci jsme potkali algoritmus pro největší společný dělitel v podobě funkce, jakou nám poradila AI. Představuje dobrou ilustraci toho
jak vypadá uvedení funkce v kódu,
jak se používá,
že je to výhodné.
[3]:
# spočtěme gcd tří čísel
def gcd(a, b):
while b != 0:
a, b = b, a % b
return a
p, q, r = 4633, 4715, 4879
c = gcd(p, gcd(q, r))
print(c)
41
V prostředí Jupyter máme funkci k dispozici od okamžiku provedení buňky obsahující zavedení funkce příkazem def. Jednak tuto funkci můžeme použít při dalším počítání, také toho ale můžeme využít v jejím testování.
[4]:
gcd(4455,9977)
[4]:
11
Definice funkce
Práce s funkcemi zahrnuje dva odlišné kroky. Samozřejmě je to zavolání funkce, podobně jako kus výrazu math.sin(x) nějak spočte sinus x a tuto hodnotu pak dále ve výrazu použijeme. Pokud ale požadujeme novou funkci, musíme dodat její definici. Tato definice říká,
co je funkci potřeba dát za informaci, aby se mohla do výpočtu pustit
jak to má udělat
Pro ilustraci použijeme jednoduchý příklad, tzv. Fibonacciho posloupnost tvořenou celými čísly \(F_0=0, F_1=1, F_k = F_{k-1}+F_{k-2}\). Její procházení je otravné, takže použijeme funkci, která se bude jmenovat fib a když jí jak argument dáme nějaké číslo \(n\) ona vrátí hodnotu \(F_n\). Pro jednoduchost tato naše první funkce vždy spočte příslušný člen posloupnosti jejím procházením znovu od začátku.
[6]:
def fib(n):
"""Počítá n-tý člen Fibonacciho posloupnosti"""
assert n>=0,"Použitý postup neumí záporné argumenty"
if n==0:
return 0;
a = 0 # inicializace lokálních proměnných
b = 1
for i in range(2,n+1):
a, b = b, a+b # jeden krok Fibonacciho řady
return b
print(fib(20))
6765
Zde nejprve pár pozorování:
Zápis definice funkce
začíná hlavičkou, která říká, jak se funkce jmenuje a jaké parametry potřebuje, aby mohla spočíst, co se po ní požaduje
dále pokračuje příkazy, s jakými jsme se již seznámili
ale je mezi nimi jeden nový příkaz
return
Seznam formálních parametrů je v závorce za identifikátorem funkce. Protože podobně jako v algebře předpokládáme, že argumenty mohou nabývat různých hodnot, označíme je identifikátory tak, aby jednou mohlo být
n==2a jindyn==20.V Pythonu stále ještě spíše není zvykem uvádět typ argumentů. (Ukážeme se, že to jde a že to má smysl)
Opět je to odsazení (indentace) textu, které určuje, jaké příkazy jsou součástí definice funkce.
Je zvykem na prvním řádku pod hlavičkou funkce uvést dokumentační řetězec. Tento řetězec se obvykle zobrazí jako nápověda, když v napíšeme název funkce. Trojité uvozovky dovolují jako mít jako součást řetězce nové řádky i uvozovky.
Je vhodné zkontrolovat parametry. Kontrola v podobě
assert n>=0kromě záporných \(n\) také vyloučí mnohé nečíselné parametry, které způsobí chybu při porovnávání s nulou. (Např.fib(True)ale testem projde a funkce nakonec vrátí hodnotu 1.)Nevadí nám, že pracujeme s velkými čísly, protože v Pythonu (ne však v numpy) mohou mít celá čísla libovolnou velikost, takže
fib(100)==354224848179261915075.Příkaz
return bzařídí, že provádění funkce se ukončí a ta vrátí (odkaz na) uvedenou hodnotu.Ani lokální proměnné se nedeklarují.
Výše definovanou funkci fib můžeme použít v dalších výpočtech:
[7]:
# demonstrace hodnot poměru sousedních členů Fibonacciho posloupnosti
phi = (1+5**0.5)/2
for k in range(5,28,5):
pomer = fib(k+1)/fib(k)
print( f"{k:3} {pomer:15.12f} {pomer-phi:9.2g}" )
5 1.600000000000 -0.018
10 1.618181818182 0.00015
15 1.618032786885 -1.2e-06
20 1.618033998522 9.8e-09
25 1.618033988670 -7.9e-11
Volání funkce
Když máme funkci fib stojí za to ověřit známou vlastnost podílu sousedních členů
k = 100
print(fib(k+1)/fib(k))
Kód sice není zrovna efektivní, ale je naprosto zřejmé, co že to má print vypsat.
Funkce fib bude volána dvakrát, jednou s argumentem 101, podruhé 100.
Důležité: Těm závorkám za identifikátorem funkce rozumějme jako spusť výpočet funkce Proto, když některé funkce nepotřebují argument, stále potřebují aspoň prázdné závorky. Příklad:
print()
vytiskne prázdný řádek. Jako příkaz bez závorek by nemělo v programu žádný efekt.
Nepovinné argumenty
Následující funkce vrací řetězec odpovídající danému celému číslu v příslušném základu pozičního zápisu čísel. U druhého argumentu má uvedenu výchozí hodnotu 10.
[1]:
def int2str(a, radix=10):
assert 2 <= radix <= 10
assert type(a) == int
if a<0:
return '-' + int2str(-a,radix)
s = ''
while True:
s = str(a%radix) + s
a = a // radix
if a==0:
break
return s
a = 97
print( int2str(a) )
print( int2str(a,10) ) # stejné jako výše
print( int2str(a,2) )
97
97
1100001
Jak příklad ukazuje, tuto hodnotu nemusíme uvádět, pokud nám výchozí hodnota vyhovuje.
Pokud má funkce více argumentů s uvedenou výchozí hodnotou,
def f(a, b=0, c=1, d=2):
print(f'{a=},{b=},{c=},{d=}')
můžeme při volání
uvést všechny v uvedeném pořadí
f(1,2,3,4)uvést jen několik prvních
f(1,2)nebof(1,2,3)uvést pojmenované argumenty
f(1,d=3)několik prvních argumentů a vybrané pojmenované
f(1,2,d=3)
Pozn. Rozmyslete si, že víte, co v každém z výše uvedených příkladů procedura f vytiskne.
Předávání argumentů
V Pythonu nemůžeme ovlivnit, jakým způsobem se funkcím předávají argumenty. Je vždy ekvivalentní přiřazovacímu příkazu. Podobně jako u přiřazení se nevytváří kopie předávaných dat ale jen další odkaz na ně. Uvidíme, že u např. u polí a seznamů to může mít nezamýšlené důsledky.
Proměnné lokální a globální
Doposud jsme uvažovali jen programy tvořené sadou příkazů bez definic vlastních funkcí. Identifikátory proměnných, které jsme v programu použili odkazovaly na proměnné, které počaly svůj život prvním přiřazením a přestaly existovat až při ukončení programu. To jsou tzv. globální proměnné.
V okamžiku zavolání funkce se odehraje důležitá změna. Kartotéka s globálními proměnnými se odsune stranou a založí se nová kartotéka, nazvěme ji kartotékou lokálních proměnných. Ta zpočátku obsahuje jen identifikátory dané seznamem argumentů funkce. Když uvnitř funkce přiřadíme do identifikátoru, který v ní není se založí nová lokální proměnná. A to i tehdy, pokud proměnná s tímto jménem je v kartotéce globálních proměnných.
Obráceně, pokud uvedme nějaký identifikátor jinde než jako cíl přiřazovacího příkazu, nejprve se hledá v kartotéce lokálních proměnných. Teprve, když se tam daný identifikátor nenajde, podívá se Python do kartotéky globálních proměnných. Samozřejmě, pokud ani tam není, jde o chybu.
Odborně se místo o kartotéky používá termín scope, řekněme rozsah (platnosti proměnných). Volání funkce tedy přepíná z globálního do lokálního rozsahu.
Někdy můžeme chtít uvnitř funkce přiřadit do globální proměnné. K tomu slouží příkaz global. Důsledky jeho použití demonstrujeme na dvojici kódů
y = 'původní y' y = 'původní y'
def f(x): def f(x):
"y bude globální" "y bude lokální"
global y
y = x y = x
print(repr(y)) print(repr(y))
f('změna') f('změna')
print(repr(y)) print(repr(y))
---------------------- ----------------------
'původní y' 'původní y'
'změna' 'původní y'
Vidíme, že ve druhém případě je y lokální proměnná a její nastavení se nedotkne globální proměnné, i když nese stejný identifikátor.
Rozbor dějů při volání funkce
Uvažujme krátký program:
[32]:
def symmetric_ratio(x,y):
"Vrací hodnotu x/y+y/x"
s = x**2+y**2
return s/(x*y)
x = 1
y = 4
print( symmetric_ratio(x,y+1), symmetric_ratio(x+1,y) )
5.2 2.5
Program obsahuje následující kroky:
Vytvoření funkce
symmetric_ratio. Jde o globální identifikátorVytvoření proměnné
xspojené s jejím nastavením na1Vytvoření proměnné
yspojené s jejím nastavením na4Spočtení hodnot
xay+1přepnutí rozsahu z globálního do lokálního rozsahu funkce
symmetric_ratiovytvoření lokální proměnné
x. Protože jde o argument, je obsazena předanou hodnotou 1.vytvoření lokální proměnné
y. Protože jde o argument, je obsazena předanou hodnotou 5.(Dokumentační řetězec se nepřekládá.)
vytvoření lokální proměnné
sa její nastavení na odpovídající hodnotu (26).spočtení
26/5vrácení této hodnoty spojené s přepnutím do globálního rozsahu
Spočtení hodnot
x+1aypřepnutí rozsahu z globálního do lokálního rozsahu funkce
symmetric_ratiovytvoření lokální proměnné
x. Protože jde o argument, je obsazena předanou hodnotou 2....
spočtení
20/8vrácení této hodnoty spojené s přepnutím do globálního rozsahu
vytisknutí obou vrácených hodnot
Přepnínání rozsahů znamená, že globální x a lokální x jsou jiné proměnné a program výše je ekvivalení následujcícímu kódu. (Jako simulaci konce existence lokálních úproměnných zde používáme příkaz del, který zruší daný identifikátor. Jinak se s ním moc nepotkáme a tak zcela stačí, pokud budete rozumnět následujcímu kódu bez oněch řádků, kde se vyskytuje.)
[33]:
# provádějí se příkazy hlavního programu
x = 1
y = 4
# výpočet a předávání argumentů prvního volání ####
param_x = x #
param_y = y+1 #
# vlastní výpočet popsaný kódem funkce ####
local_s = param_x**2+param_y**2 #
result = local_s/(param_x*param_y) #
# konec existence lokálních proměnných i argumentů #
del param_x, param_y, local_s #
# konec běhu funkce ####
print_arg1 = result
del result
# výpočet a předávání argumentů druhého volání ####
param_x = x+1 #
param_y = y #
# vlastní výpočet popsaný kódem funkce ####
local_s = param_x**2+param_y**2 #
result = local_s/(param_x*param_y) #
# konec existence lokálních proměnných i argumentů #
del param_x, param_y, local_s #
# konec běhu funkce ####
print_arg2 = result
del result
print(print_arg1,print_arg2)
del print_arg1, print_arg2
5.2 2.5
Funkce nebo procedura?
Zrovna na příkazu print vidíme, že exitují funkce, které nic nevrací. V Pythonu je tohle nic speciální hodnota None.
Všimněte si, že hlavička definice nerozlišuje, zda jde o funkci nebo proceduru, vždy je použito def. Toto rozlišení nastane v rámci příkazů uvnitř funkce:
Funkce obsahuje příkaz
returnbez "argumentu"Funkce končí bez příkazu na konci
Obě tyto situace jsou ekvivalentní provedení příkazu
return None
Zde je příklad kombinující obě tyto možnosti:
def print_fib(n):
if n<0:
print('Neumím záporná n')
return
print(fib(n))
Kdybychom příkaz return vynechali, funkce by sice napsala 'Neumím záporná n', ale následovalo by stejně volání funkce fib a ta by pak ohlásila chybu díky příkazu assert.
Často nemívají procedury žádný return, protože nepříjemné situace jsou ošetřeny příkazem assert.
[21]:
def print_triangle(n):
"""Vytiskne trojúhelník z 1,3,5,..n resp. 2,4,6,..,n hvězdiček"""
assert n>0 and type(n)==int, "Argument print_triangle(n) musí být celé kladné číslo"
for k in range((n-1)%2+1,n+1,2):
print(' '*((n-k)//2) + '*'*k)
print_triangle(5)
*
***
*****
Lokální proměnné a procedurální programování
Lokální proměnné jsou klíčovou součástí procedurálního programování. Program rozdělíme na menší podproblémy, a když při jejich řešení potřebujeme stav mezivýpočtů někam uložit, neobtěžujeme s tím ostatní. Používáme proměnné, jejichž efekty jsou omezeny jen na tuto funkci.
Důvod pro to je velmi praktický - u složitějších programů je pracné hlídat nezamýšlené interakce mezi jeho jednotlivými částmi a lokalita proměnných tohle usnadňuje. V Pythonu se takové výhody soustředí zejména na to, že pokud explicitně neoznámíme, že chceme modifikovat globální proměnnou, uvnitř funkce vytváříme a nadále modifikujeme pouze soukromou (lokální) proměnnou, která se klidně může jmenovat jako důležitá proměnná globální. Až se seznámíme se statickou kontrolou typů, uvidíme, že i zde jsou lokální proměnné pohodlnější, protože je tím snazší udržet typ konzistentní proměnné, čím kratší je doba jejího života.
První vlastnost si ilustrujme na jednoduchém příkladu. Bývá zvykem celočíselnou proměnnou označovat i. Proto dává smysl psát
def sum100(n):
s = 0
for i in range(0,2*n,2):
s = s+10**i
return s
i = 10
while i>0:
print(sum100(i))
i = i-1
kde používáme i jak v hlavním programu tak ve funkci sum100. Pokud by i nebylo v rámci funkce sum100 lokální proměnnou, nechoval by se program správně. Snadno se přidáním řádku global i na začátek sum100 přesvědčíme.
Lokální vs globální proměnné
Víme, že přiřazením do doposud nepoužitého identifikátoru vzniká nová proměnná. Dalším přiřazením se pak mění její hodnota.
Obě tato pravidla musíme nyní upřesnit.
Přiřazením do identifikátoru doposud nepoužitého uvnitř funkce vzniká nová lokální proměnná.
Pokud přiřadíme do identifikátoru, který již existuje pro globální proměnnou, stejně zakládáme proměnnou lokální a tato onu proměnnou globální uvnitř funkce zastíní.
Použitím identifkátoru globální proměnné (nikoli ovšem přiřazením do něj) používáme onu globální proměnnou. U jednoduchých reálných a celočíselných proměnných tedy můžeme přečíst jejich hodnotu ale nikoli ji změnit. U polí to bude časem složitější.
Chceme-li z vnitřku funkce přiřazením změnit globální proměnnou, musíme tento náš záměr učinit zjevným použitím příkazu
global
Protože v interaktivním režimu (např. Jupyter) můžeme i po havárii funkce zadávat další příkazy, přináší mofifikace globálních proměnných z vnitřku procedur a funkcí riziko. Když totiž taková funkce havaruje např. v důsledku špatných hodnot argumentů, může zanechat globální proměnné v porušeném, nekonzistentním stavu. V takovém případě musíme před další prací uvést globální proměnné do vhodného stavu.
Stejně jako v jiných jazycích můžeme překlepem odkázat na nějakou existující globální proměnnou místo proměnné zamýšlené. V Pythonu je to ale častější problém, protože uvnitř funkce máme přístup ke všem právě existujícícm globálním proměnným.
Životní cyklus proměnných
V Pythonu je život proměnných určen časem provádění příkazu, nikoli řádkem, na kterém je uveden.
Globální proměnná začne existovat prvním přiřazením do daného identifikátoru. Od tohoto okamžiku ji mohou používat další příkazy hlavního programu a všechny jím volané funkce v libovolné hloubce. Globální proměnná existuje, dokud program neskončí (nebo ji neodstraní příkaz
del).Lokální proměnná začíná existovat prvním přiřazením do daného identifikátoru uvnitř funkce. Její život končí příkazem return nebo posledním řádkem procedury. (Neprobíráme vnořené funkce a příkaz
nonlocal.)
V běžných jazycích představují proměnné jen jména známá překladači a určující pojemnování kousků paměti. V přeloženém programu pak z proměnných zůstanou jen čísla paměťových buněk. Jejich jména jsou případně potřeba jen pro ladění programu. V Pythonu je proměnná něco jako položka v telefonním seznamu účastníka divoké párty. Jak program běží, objevují se nové položky v seznamu proměnných. Aktuálí seznam proměnných získáme voláním funkce dir().
Příkaz def
Narozdíl od jazyků jako je C nebo Fortran je v Pythonu definicce funkce aktivní příkaz. Podobá se příkazu přiřazovacímu. Například
q = x + y
spočte hodnotu x+y, tato spočtená data se někde nachází a na tuto spočtenou hodnotu přiřazení namíří odkaz vedoucí z identifikátoru q. Podobně
def p(x,y):
return x + y
přeloží kód funkce (vyzvedni x, vyzvedni y, sečti a vrať). Takto přeložený kód (=data) se někde nachází a def na tento kód namíří odkaz vedoucí z identifikátoru p.
Tento detail se projeví v okamžiku, kdy funkce obsahuje nepovinné argumenty, jejichž hodnota je určena výsledkem volání jiné funkce, řekněme
def hmotnost_kulicky(polomer, material = hustota_materialu("ocel"))
...
V tom případě se funkce hustota_materialu zavolá v okamžiku, kdy provádění kódu dorazí na řádek s def hmotnost_kulicky nikoli až když funkci voláme, např. print( hmotnost_kulicky(0.4) ) .
Podobně jako do stejné proměnné můžeme několikrát přiřadit a je to poslední přiřazení, které nakonec určuje hodnotu proměnné, můžeme vícekrát po sobě definovat stejně se jmenující funkci, přičemž platí naposled provedená definice funkce.
Funkce jako argument jiné funkce
Důležité je rozumět dvěma velmi odlišným přiřazením:
u = math.sin(x)
v = math.sin
Obě přiřazení jsou platné příkazy. Po jejich provedení * u bude hodnota sinu x, takže bude rozumné použít příkaz print(u) a vytiskneme tak hodnotu u, * v bude funkce, takže bude rozumné použít příkaz print(v(y)), čímž spočteme sinus y, který pak vytiskneme.
Tento rozdíl je důležitý právě v situacích, jaké fyzik při programování snadno potká. Řekněme, že chceme numericky počítat hodnotu určitého integrálu \(\int_0^\phi \sin(x) dx\). Mohlo by nás napadnout, že toho dosáhneme zavoláním vhodné funkce a vypsáním výsledku takto:
print( integral(math.sin(x),0,phi) ) # tohle je špatně
Toto je špatně, přičemž mohou nastat dvě typické situace
proměnná
xexistuje a má číselnou hodnotu, takže se spočte její sinus. To je nějaké číslo, které ale nic neříká o tom jaké hodnoty má sinus jinde a nelze z něj tedy spočíst hodnotu určitého integrálu.proměnná
xneexistuje nebo nemá číselnou hodnotu, takže dojde k chybě při výpočtu sinu.
Aby totiž mohla vůbec funkce integral spočíst hodnotu určitého integrálu, musí se ve vhodných bodech zeptat integrované funkce, jaká je její hodnota. Na takové ptaní musí specifikovat hodnotu argumentu a funkci pak zavolat. V Pythonu toho lze dosáhnout snadno, jak ukáže následující příklad.
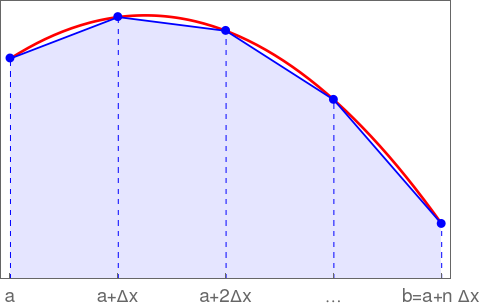
Ještě si vyložíme, jak spočíst určitý integrál, zatím to berte tak, že napíšeme funkci, která spočte přibližnou hodnotu \(\int_{-1}^1\sqrt{1-x^2}dx\). Uěláme to tak, že funkce vyska_pulkruznice bude vracet hodnotu integrandu a funkce integral bude počítat přibližnou hodnotu určitého integrálu libovolné funkce, kteru dostane jako svůj první argument. Udělá to tak, že spočte součet hodnot integrandu ve vhodných bodech integračního intervalu a součet pak vynásobí délkou dílku (například
setiny), na který interval rozdělíme. (Až si vyložíme lichoběžníkovou metodu, uvidíme, proč se v součtu objeví průměr hodnot na krajích intervalu, zatím jen obrázek, ilustrující modrými puntíky, ve kterých bodech funkce integral volá funkci f)
[3]:
import math
def integral(f, a, b, n=100):
"Spočte integral f(x) dx pro x=a..b lichoběžníkovou metodou"
dx = (b-a)/n
soucet = (f(a) + f(b))/2
for i in range(1,n):
x = a + i*dx
soucet = soucet + f(x)
return dx*soucet
def vyska_pulkruznice(x):
return math.sqrt(1-x*x)
# zkusíme spočíst pi jako dvojnásobek plochy pod kružnicí
print( 2*integral(vyska_pulkruznice,-1,1, n=1000) )
3.141487477002142
Protože předávání argumentu je podobné přiřazení f = vyska_pulkruznice, takže uvnitř funkce integral argument f se chová jako funkce, přičemž zastupuje předanou funkci.
Po dobu běhu funkce integral bude první argument nabývat hodnoty vyska_pulkruznice, nebo např sinus, když, abychom ověřili, že funkce počítá správné hodnoty, zkusíme vyčíslit integral(math.sin,0,math.pi) a jindy, řekněme, rychlost_castice, což bude námi napsaná funkce jedné proměnné, když budeme chtít spočíst dráhu. Nyní se jen musíme naučit správnou numerickou metodu, napsat lepší variantu funkce integral a budeme umět integrovat libovolnou (hezkou) funkci. Bude to podobné, jako
správně napsaná funkce sinus umí spočíst jeho hodnotu pro libovolné \(x\).
Poznámka: To, že funkce jsou vlastně proměnné odkazující na objekt typu funkce vysvětluje, jak máme chápat výstup příkazu
print(fib)
Vypadá to, žde jde o chybu a nejspíš jsme zapomněli uvést argument. Jenže Python to jako chybu nechápe a rád odpoví
<function fib at 0x3243f48>
To divné číslo říká, kde v paměti jsou informace o přeložené funkci uložena. To, že jsou poměrně komplexní ukáže například to, že obsahují atribut __doc__:
print(fib.__doc__)
tedy vypíše
'Počítá n-tý člen Fibonacciho posloupnosti'
Rekurze
Zajímavou možnost v procedurálním programování představuje rekurzivní volání. Rozumí se tímsituace, kdy
funkce f volá samu sebe
funkce f volá další funkci, která sama nebo skrze ještě další funkce zavolá opět f
Nejprve si vše ilsutrujeme na obvyklém příkladě, kterým je faktoriál funkce, protože ten splňuje
$:nbsphinx-math:displaystyle n ! = n (n-1)! $
Následující program tuto vlastnost využívá:
[3]:
def faktorial(n):
if n<=1:
return 1
n1f = faktorial(n-1)
return n*n1f
f = faktorial(7)
print(f)
5040
Především, aby rekurzivní výpočet mohl skončit, je nezbytné, aby funkce obsahovala větev, která rekurzi nepoužívá a aby u ní výpočet časem skončil.
Druhým důležitým předpokladem je zajímavý charakter lokálních proměnných, o kterém jsme dosud nemluvili. Nejen, že lokální proměnné a argumenty funkce existují jen po dobu jejího volání, ale v případě, že funkce zavolá sama sebe, vnikne nová sada argumentů a lokálních proměnných (chovají se stejně, jen argumenty se inicializují při volání zatímco lokální proměnné až za běhu funkce.)
Abychom si popsali, co se při rekurzi děje, musíme na chvíli připustit, že při své činnosti program není naplňován po řádcích ale po instrukcích. (Nevadí zde, že v Pythonu nejde přímo o instrukce procesoru počítače.) Zjednodušený seznam instrukcí našeho krátkého programu pro vypsání \(7!\) je
# def faktorial(n):
# if n<=1:
10 LOAD (n)
11 LOAD_CONST (1)
12 COMPARE_OP (<=)
13 JUMP_IF_FALSE (to 16)
# return 1
14 LOAD_CONST (1)
15 RETURN_VALUE
# n1f = faktorial(n-1)
16 LOAD (n)
17 LOAD_CONST (1)
18 BINARY_OP (-)
19 CALL (faktorial)
20 STORE (n1f)
# return n*n1f
21 LOAD (n)
22 LOAD (n1f)
23 BINARY_OP (*)
24 RETURN_VALUE
# f = faktorial(7)
30 LOAD_CONST (7)
31 CALL (faktorial)
32 STORE (f)
# print(f)
33 LOAD (f)
34 CALL (print)
Číslo na začátku řádku označuje pořadí instrukce, jak je uložena v paměti, velkými písmeny jsou symbolické názvy každé operace/instrukce, v závorkách pak jejich argumenty/operandy. Povšimněte si, že instrukce skoku a volání mají jako argumenty pořadí instrukcí, kde má výpočet pokračovat. ( Více nebudeme potřebovat, ale protože fyzika často zajímá, "jak to funguje", ještě pár slov: Instrukce předpokládají jakýsi zásobník, kam se operacemi LOAD ukládají hodnoty a operacemi jako je *, -
nebo <= se ze dvou hodnot na vrcholu zásobníku stane jedna. Tu lze pak vyzvednout instrukcí STORE a uložit do proměnné. Po provedení instrukce RETURN_VALUE zůstane tato hodnota na vrcholu zásobníku. )
Z hlediska pochopení průběhu volání při rekurzi nás zajímá jen instrukce CALL. Jde o volání funkce. V programu se vyskytuje 3\(\times\). Jedenkrát se volá funkce print a na dvou místech se volá funkce faktorial. To je důležité, protože je na místě se ptát, jak to program dělá, že se při provádění instrukce návratu z funkce (RETURN_VALUE) výpočet vrátí na instrukci za tím správným CALL. Zjednodušená odpověď je, že mezi lokálními proměnnými každé funkce je ještě jedna
skrytá, říkejme jí return_address, která je instrukcí CALL nastavena tak, že instrukce návratu z funkce si tuto hodnotu může přečíst a pokračovat prováděním instrukce za tím správným CALL.
Následující tabulka schematicky zachycuje stav těchto individuálních lokálních dat v okamžiku, kdy zrovna funkce faktorial volaná s n=3 spočetla \(2!\), uložila tuto hodnotu do lokální proměnné n1f a chystá se ji vynásobit 3 (to je hodnota n) a vrátit tento součin:
n |
n1f |
return_address |
|---|---|---|
7 |
32 |
|
6 |
20 |
|
5 |
20 |
|
4 |
20 |
|
3 |
2 |
20 |
Slovní popis tabulky je
hlavní program zavolal faktorial(7)
. funkce faktorial s hodnotou argumentu n=7 spočetla 7-1 a zavolala faktorial(6)
... funkce faktorial s hodnotou argumentu n=5 spočetla 5-1 a zavolala faktorial(4)
.... funkce faktorial s hodnotou argumentu n=4 spočetla 4-1 a zavolala faktorial(3)
..... funkce faktorial s hodnotou argumentu n=3 spočetla 3-1, zavolala faktorial(2), dostala výsledek a ten uložila do n1f
Důležitý poznatek: při rekurzivním volání funkcí existuje tolik nezávislých sad lokálních proměnných, jaká je hloubka rekurze. Součástí stavu výpočtu funkce pak je i informace, kde má výpočet pokračovat, až bude funkce hotová. To samozřejmě platí i bez rekurze, protože tatáž funkce může být volána z různých míst programu a je nezbytné, aby pokračovala ve výpočtu přesně za tím místem (instruckí call), kde jsme o výpočet hodnoty funkce požádali. ( Protože lokální proměnné zabírají nějaké místo,
pak pokud je počet opakování rekurzivního volání velký, může výpočet havarovat pro nedostatek takové paměti - zásobníku. Python konkrétně ohlásí RecursionError: maximum recursion depth exceeded.)
Poznámka: Toto je jedno z míst, na které míří počítačoví záškodníci. Pokud se jim podaří paměť modifikovat tak, aby se po skončení výpočtu nějaké funkce program vrátil jinam než je zamýšleno (řekněme místo zpět do funkce stav_konta do vhodného místa funkce pripis_na_konto), mohou napáchat rozličné škody.
Jako další ukázku rekurzivního algoritmu použijeme výpis celého čísla v pozičním systému. Jde o to, že například číslo n=5471 lze vypsat tak, že nejprve vypíšeme n//10 = 547 a potom n%10 = 1. Rekurze se pak objeví přirozeně, protože stejný postup aplikujeme na číslo 547. Totéž platí i ve dvojkové či hexadecimální soustavě. Jako obvykle u hexadecimálního zápisu použijeme písmena a-f pro hexadecimální cifry 10-15. Za tím účelem se v kódu objeví chr( ord('a') + c-10 ), tedy znak
s kódem ord('a') plus o kolik je cifra c větší jak 10.
[9]:
def print_i2(i, end='\n'):
assert i>=0
if i>2:
print_i2(i//2, end='')
print(i%2, end=end)
print_i2(253)
#########
def print_i10(i, end='\n'):
assert i>=0
if i>10:
print_i10(i//10, end='')
print(i%10, end=end)
print_i10(253)
############
def print_i16(i, end='\n'):
assert i>=0
if i>16:
print_i16(i//16, end='')
c = i%16
if c>9:
c = chr( ord('a') + c-10 )
print(c, end=end)
print_i16(253)
11111101
253
fd
Úloha - Procvičení nepovinných argumentů funkcí
Změňte hlavičku funkce
print_i10nadef print_i10(i, end_char='\n'):(tedy přejmenujte druhý argument této funkce) a následně pozměňte vnitřek funkce, tak aby fungovala jako doposud
Následně změňte hlavičku funkce
print_i10nadef print_i10(i, end_char):(tedy vynechte automatickou hodnotu druhého argumentu) a příslušně upravte její použití, aby dávalo stejné výsledky jako doposud
Úloha - Zobecněte všechny tři funkce do jediné s dodatečným argumentem radix, jehož výchozí hodnota je 10, která zkontroluje, že jeho hodnota je mezi 2 a 36 a pak číslo vypíše.
 Programování pro fyziky (1.r)
Programování pro fyziky (1.r) Obsah
Obsah