Pole a seznamy
Než si ukážeme klíčové příklady použití polí, seznámíme se s antickým algoritmem pro pořízení seznamu prvočísel:
Eratosthenovo síto
Eratosthenes z Kyrény nám radí vyškrtat ze seznamu všech celých čísel nulu (Pythonu nás nutí brát nulu jako první celé číslo), jedničku a pak všechny dvou- a více- násobky původně nevyškrtnutých čísel. Co zbyde nevyškrtnuté je prvočíslo.
V následujícím kódu máme funkci, která vrací pole informací o tom, zda číslo \(i\) je prvočíslo. To má podobu tabulky
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
... |
|---|---|---|---|---|---|---|---|---|---|---|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
... |
V tabulce je na horním řádku pořadové číslo v poli/seznamu - tzv. index a ve spodním řádku je pak hodnota určená indexem. V matematice to zapisujeme \(a_i\). Povšimněte si, že index je celé číslo a hodnoty jsou stejného typu. Takovouto organizaci dat v programu nazýváme pole.
Představujeme si, že tahle tabulka nějak bydlí v paměti počítače (podrobněji dále) a když zadáme index, počítač se umí podívat, jaká hodnota indexu přísluší. Tato operace se nejen v jazyce Python zapisuje promenna[i]. Index i je podle této představy celé číslo, přičemž Python spadá to té podmnožiny počítačových jazyků, kde se prvním prvkem pole/seznamu rozumí ten s indexem 0, tedy promenna[0].
Následující kód definuje a volá funkci eratosthenes(n). Jak víte malé e píšeme nikoli z neúcty, ale proto, že úzus použitého jazyka rezervuje identifikátory počínající velkým písmenem pro třídy (a konstanty).
[1]:
import numpy as np
def eratosthenes(n):
"""Vrací pole [False,False,True,True,False,True,...] délky n+1
indikující, že mezi čísly 0..n jsou 2,3,5,... prvočísla"""
je_prvocislo = np.full(n+1, True)
je_prvocislo[0] = False
je_prvocislo[1] = False
p = 2
while p*p <= n:
if je_prvocislo[p]:
for nasobek_p in range(2*p,n+1,p):
je_prvocislo[nasobek_p] = False
p = p + 1
return je_prvocislo
n_max = 35
vysledek = eratosthenes(n_max)
print( vysledek )
print( "\nNalezená prvočísla:")
for i in range(n_max+1):
if vysledek[i]:
print(i, end=' ')
[False False True True False True False True False False False True
False True False False False True False True False False False True
False False False False False True False True False False False False]
Nalezená prvočísla:
2 3 5 7 11 13 17 19 23 29 31
Sám algoritmus je v kódu snadno čitelný. Má za úkol demonstrovat, jakým způsobem budeme v jazyce Python pracovat s poli. Není to způsob jediný, ale poskytne nám nejméně náročnou a ve světě programování pro fyziky běžnou představu o práci s poli.
Již první řádek říká, že budeme používat knihovnu numpy. Protože jsme zvyklí, že i pro funkci sinus musíme do nějaké knihovny, není to úplně překvapivé. Je ale třeba hned přiznat, že Python má jiný základní typ pro pole a seznamy, který nevyžaduje další knihovny. Jen se nám tolik nehodí vzhledem k omezenému rozsahu naší přednášky.
Příkaz
import numpy as np
říká, že chceme používat knihovnu numpy, ale místo (např.) numpy.sin chceme psát kratší np.sin.
Program výše je rozdělen na funkci a kus programu, který funkci volá a vypisuje výsledky. Takto definovaná funkce nám dovolí ji použít dále ve výkladu.
Protože celých čísel je nekonečně, parametr n funkce určuje, u jakého největšího čísla budeme prověřovat prvočíselnost. Uvnitř funkce je nejdůležitější řádek
je_prvocislo = np.full(n+1, True)
Dává vzniknout lokální proměnné v podobě pole \(n+1\) hodnot True. S touto proměnnou pak funkce celou dobu pracuje a tu i vrátí jako výsledek.
Jak se na proměnnou sluší, můžeme ji modifikovat, proto v dalších dvou řádcích nastavíme, že čísla \(0\) a \(1\) nejsou prvočísla. Např. je_prvocislo[0] = False změní první položku pole, která byla původně inicializována na True.
Následuje Eratosthenovo vyškrtávání:
pro všechna čísla
p,pokud nejsou moc velká (pak cyklus ukončíme),
a pokud je
pprvočíslo,vyškrtneme všechny jeho násobky,
které představují platné indexy pole
je_prvocislo, protorange(2*p,n+1,p).
Vyškrtané pole, obsahující `True`` jen na místě prvočísel pak funkce vrátí.
Vraťme se ještě jednou k volání funkce np.full(n+1, True). Tušíme, že číslo \(n\) nemusí být malé a tedy samotné vytváření pole není samozřejmou operací.Někde v paměti musí být potřebné místo. Zde se projeví klíčová vlastnost knihovny numpy. Ta poskytuje pole tvořená určeným počtem prvků téhož typu. Typ prvků nelze měnit, musíme jej znát dopředu. Počet prvků je také lepší neměnit. Z hlediska spotřeby paměti je velikost pole dána součinem počtu prvků a velikosti jednoho prvku. (Pro
pokročilejší: odhad počtu bytů potřebných pro uložení proměnné x typu numpy.ndarray spočteme jako součin atributů x.size * x.itemsize.)
Výsledek, který funkce eratosthenes vrátí, kód výše použije k vypsání prvočísel \(p \le n_\text{max}\). Kód obsahuje podmíněný příkaz if vysledek[i]: který testuje, zda prvek pole s indexem i zastupuje prvočíslo a je tedy vhodné jej vytisknout. (Často lze potkat i ekvivalentní zápis if vysledek[i]==True:.)
Pole a seznamy jsou velmi podobné struktury. Abychom si to přiblížili, demonstruje následující funkce pořízení seznamu prvočísel. I když jde o tutéž informaci, jakou vrací funkce eratosthenes, její podoba je dost odlišná. Zapsána jako tabulka vypadá takto
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
... |
|---|---|---|---|---|---|---|---|---|---|---|
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
... |
[ ]:
def seznam_prvocisel(n):
"""Vrací seznam prvočísel <= n typu numpy.ndarray"""
e = eratosthenes(n)
count = 0
for i in range(n+1):
if e[i]:
count += 1
seznam = np.full(count, 0)
j = 0
for i in range(n+1):
if e[i]:
seznam[j]=i
j += 1
return seznam
seznam25 = seznam_prvocisel(25)
print(seznam25)
n_max = 1_000_000
print('Počet prvočísel <=',n_max,'je',len(seznam_prvocisel(n_max)))
[ 2 3 5 7 11 13 17 19 23]
Počet prvočísel <= 1000000 je 78498
Tento kód demonstruje možný postup konverze pole logických hodnot je/není prvočíslo na seznam prvočísel. Protože u polí, jak se je učíme, musíme před jejich vytvoření vědět, jak jsou velká, funkce seznam_prvocisel hned poté, co zavolá funkci eratosthenes, spočte, kolik prvočísel ve vráceném poli je. Učiní tak v rámci cyklu v indexu i, kdy projde všechny prvky pole e[i] a kdykoli narazí na True, zvětší proměnnou count o jednu.
Z pedagogických důvodů tedy funkce seznam_prvocisel opět používá jen dvě důležité operace
vytvoření pole funkcí
np.fullpřístup k prvku pole
e[i],seznam[j]
S nimi zkusíme vystačit, jak jen to půjde.
Snadno bychom to mohli učinit jediným příkazem, např. count = np.count_nonzero(e), protože knihovna numpy obsahuje více jak 500 různou měrou užitečných funkcí a mezi nimi je i funkce numpy.count_nonzero. Poměrně často lze za pomoci dokumentace a/nebo editoru IDE funkci provádějící žádanou operaci pohodlně nalézt a použít správné argumenty. My se ale používat numpy učíme, takže strpíme, že mnohé z funkcí, které v našem kurzu píšeme, jsou již napsané a dostupné v některé z
knihoven. V tomto případě bychom vlastně ani znalost funkcí knihovny numpy nepotřebovali, protože počet prvočísel v poli e lze zapsat i jako count = sum(e).
Pro čtenáře znalého typu list doplňuji dvě další podoby funkce seznam_prvocisel:
[ ]:
def prime_list1(n):
"""Vrací seznam prvočísel <= n typu list"""
e = eratosthenes(n)
seznam = []
for i in range(n+1):
if e[i]:
seznam.append(i)
return seznam
def prime_list2(n):
"""Vrací seznam prvočísel <= n typu list"""
e = eratosthenes(n)
return [i for i in range(n+1) if e[i]]
assert len(prime_list1(1000000)) == len(prime_list2(1000000)) == 78498
Ačkoli list je základním typem jazyka Python, námi používané pole budou dána datovým typem numpy.ndarray (z angl. n-dimensional array). Ten je spolu se desítkami/stovkami užitečných funkcí k dispozici v knihovně numpy; v rámci kurzu budeme samozřejmě používat jen naprosté minimum z nich.
Svými vlastnostmi se pole z knihovny
numpyvíce podobají polím, jaká se používají v ostatních jazycích (C, Fortran, ...).Jejich použití pro výpočty ve fyzice je mnohem běžnější.
Dále tedy budeme používat slovo pole jako synonymum pro numpy.ndarray.
Pole - celek a část. Přístup k prvku pole (a[i])
Pole představuje celek složený z více stejných prvků. Podle okolností budeme chtít:
Pracovat s celkem (např.
print(seznam25)).Pracovat s jediným prvkem (např.
seznam[j]=i)Pracovat s několika prvky najednou (viz řezy polí dále)
Přístup k prvku pole, tedy možnost pracovat s jediným prvkem pole je důležitý krok v principu programovacího jazyka. Je-li prvek např. reálné číslo a jazyk poskytuje nástroje pro práci s takovými čísly (např. sčítání), dokážeme opakováním takových operací u každého prvku např. sčítat vektory. Prvek pole můžeme nastavovat i číst.
Nastavení prvku pole jsme viděli u Eratosthenova algoritmu, kde bylo potřeba jej nastavit tak, aby signalizoval, že dané číslo není prvočíslo. Takováto operace změny prvky má většinou podobu přiřazení, tedy a[i] = nova_hodnota.
Obrácená operace, tedy čtení hodnoty prvku se zapisuje stejně, ale tato kombinace identifikátoru pole a indexu v hranatých závorkách se objevuje v nějakém výrazu. Může jít např. o aritmetický výraz na pravé straně přiřazovacího příkazu nebo o logický výraz, který se objevuje v příkazech if, while atd.
Připomeňme, že v hranatých závorkách se může vyskytovat libovolný celočíselný výraz, jehož hodnota padne do mezí stanovených počtem prvků pole. Například výraz a[i+1]*a[i-1]==a[i]**2 může být součástí testu, zde se posloupnost chová jako geometrická řada. Při takovém testu ale nesmíme zapomenout, že hodnoty indexu i musejí splňovat i>0 a i+1<len(a).
První položka pole má index 0
Jazyky jako je Python, C, Java, .... nám vnucují, že první položka pole má index 0. Tedy v kódu funkce eratoshenes příkaz je_prvocislo[0] = False nastavuje první prvek pole.
Je snadné si na to zvyknout, jenže bohužel pravděpodobně budete zároveň pracovat v jazycích (Fortan, Mathematica, Matlab), kde je počáteční index jednička. I na toto neustálé střídání konvencí si nakonec zvyknete (budete muset).
Bereme na vědomí typy list a tuple
Již víme, že pole budou užitečná. Jsou natolik užitečná, že se v Pythonu vyskytují dva základní typy polím velmi podobné. Protože nemůžeme stihnout jejich vlastnosti ani povrchně probrat, ale zároveň jsou v jazyce Python příliš všudypřítomné, shrneme si aspoň nejzákladnější informace.
Společnou vlastností ndarray, list, tuple je možnost vybrat prvek pomocí hranatých závorek, např. a[i+1].
Typ
listvytvoříme, když napíšeme seznam libovolného (i nulového) počtu hodnot do hranatých závoreka = [1,2,3]
Typ
tuplevytvoříme, když napíšeme seznam hodnot do kulatých závoreka = (1,2,3)
Protože jedna hodnota v závorce má význam uzávorkovaného výrazu, je nutné psát před zavírací závorkou čárku
a1=(1,). Kdybychom to potřebovali lze prázdnýtuplepsáta0=().Na rozdíl od typu
listnelze do jednotlivých prvkůtupledosadit nové hodnoty. Právě kvůli této odlišnosti byl tento typ zaveden, v jazyku Python to hraje důležitou roli.Typ
tuplejsme již potkali, protože funkce, které vracejí více hodnot, vracejí ve skutečnosti právě typtuple. Ačkoli jsme si navykli na pohodlnější způsob psaníreturn x,y, ten je ekvivalentní explicitnímu uvedení kulatých závorekreturn (x,y).Kontrolní otázka: U builtin funkce
divmod(a,b)si můžeme představovat, že končí příkazemreturn a//b, a%b. Jaký výsledek očekáváte u příkazuprint( type( divmod(7,4) ) )?
Unpacking
Byli jsme zvyklí u funkcí, které vracejí více hodnot použít vícenásobné přiřazení
podil, zbytek = divmod(p,q)
Jde o speciální případ procesu zvaného unpacking, který má např. pro tři hodnoty podobu
prom1, prom2, prom3 = seznamu_podobny_vyraz
Na pravé straně může být cokoli, co má tři části: ndarray, list, tuple, range, .... Pokud počet hodnot na levé a pravé straně nesouhlasí, dojde k chybě.
Pole nebo seznam?
Ještě jednou se vrátíme k odlišnostem mezi polem a seznamem. Ten není úplně zřetelný, jak demonstruje příklad výše, kde v obou případech používáme tentýž typ numpy.ndarray.
Pole
V problémech souvisejících s fyzikou budeme spíše potkával pole. Polem obvykle rozumíme sadu prvků stejného typu naskládaných do jednoho celku, přičemž celkový počet prvků tvořících pole je obvykle předem známý. Např. u funkce eratosthenes výše určujeme nejprve délku pole, které funkce vrací. Během výpočtu pole naplníme informací o tom, zda dané celé číslo je prvočíslem.
Se kterým z prvků chceme pracovat určujeme indexem, takže místo identifikátoru proměnné, např. x, který jsme používali ve výrazech nebo na pravé straně přiřazovacího příkazu píšeme například a[i+1], kde a je identifikátor proměnné typu pole a i+1 je příklad celočíselného výrazu, který dává hodnotu indexu určujícího, se kterým prvkem pole míníme pracovat. Celý příkaz může mít například podobu
soucet = soucet + a[i]*b[i]
Pokud konkrétně tuto operaci provedeme pro všechny prvky stejně dlouhých polí a a b (a pokud je sčítací proměnná na začátku vynulovaná) spočteme takto skalární součin dvou vektorů
Pole se dvěma indexy kromě matic může také představovat obrázek, tzv. bitmapu. Obrázky mohou mít různé šířky a výšky (počítáno pixely), ale cítíme, že obrázek není seznam pixelů.
Seznam
Další funkce seznam_prvocisel(n) naopak obsahovala čísla, nikoli logické hodnoty. Tato čísla (v souladu s názvem funkce) představovala (seřazený) seznam prvočísel \(\le n\). To mělo ilustrovat odlišnost mezi polem a seznamem.
Tedy, seznamem můžeme mít jednak obecně na mysli data, kde informace, v nich obsažená, zahrnuje také délku seznamu a dává dobrý smysl do seznamu několik položek přidat a délku tak změnit. A i po takové změně má stále smysl se např. ptát kolik položek je dvou seznamech stejných. Oproti tomu pole obecně jsou spíše podobná vektorům, kde nemůžeme změnit dimenzi \(\vec x\) ze 3 na 5 a \(\vec y\) ze 3 na 7 a tvářit se, že jsme jen něco přidali. Zkuste nyní spočítat \(\vec x\cdot \vec y\)!
Seznamem však také můžeme konkrétně mínit typ list, jak jsme zmínili, jde o jeden ze základních typů, jaké Python nabízí. Ten je většinou vhodnější pro pořizování seznamů (v obecném smyslu výše) než pole knihovny numpy, na která se v kurzu soustředíme. Typ list budeme v kurzu používat co nejméně. Sice tím přijdeme o zajímavou část jazyka Python, ale mnohé odlišnosti list od `numpy`` polí jsou dost matoucí a v rámci výuky musíme dát přednost srozumitelnosti. TODO: Rozmyslet, zda
poznámky k typu list dávat do textu průběžně nebo do kapitolky na konec.
Proto, i když to přinese delší kód, budeme i seznamy ubytovávat v polích z knihovny numpy.
Vytvoření pole (numpy.full a další)
Připomeňme si, že proměnné v Pythonu odkazují na data, jaká jim přiřadíme a podobně je to i s argumenty funkcí. Pole, se kterými chceme pracovat se tedy nejprve někde musejí vzít, abychom je mohli svázat se jménem nějaké proměnné a s její pomocí je dále zpracovávat nebo obrábět.
Mezi spoustou možností, jak vytvořit pole zmiňme jako nejdůležitější tuto:
my_array = numpy.full( count, fill_value )
Pokud například bude count==10 a fill_value==2, bude my_array odkazovat na takovouto tabulku čísel:
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|---|---|---|---|---|---|---|---|---|---|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
Snadno se o tom přesvědčíme příkazem print( my_array ).
Důležitá vlastnost polí z numpy je to, že typ hodnot v nich uložených je určen v okamžiku vzniku pole. Nyní jsme zvolili celé číslo a tak v dalších operací můžeme měnit hodnoty prvků, ale nemůžeme měnit jejich typ. Navíc se o této vlastnosti dozvíme jen z toho, že výsledek operace nebude totožný s naším přáním. Například my_array[3] = math.pi bude provedeno jako my_array[3] = int(math.pi), tedy ve čtvrtém prvku pole se objeví celé číslo 3.
Shrnuto, s použitím numpy se kód
my_array = np.full( 4, 2 )
chová podobně jako např. v C
int my_array[4] = {2,2,2,2};
tedy určuje typ prvků pole a jejich počet. (Kdybychom v kurzu probírali podrobněji typ list, viděli bychom, že zde je možno mít v poli prvky různých typů a dokonce jejich typ měnit za běhu programu.)
Cvičení: Vytvořte pole pole_3x1 o délce 3 a naplněné hodnotou 1.0. Co bude výstupem příkazu print( pole_3x1 )? Jak se liší od situace, kdybychom měli pole tří celých čísel 1?
Vytvoření pole - další možnosti
V našem kurzu bychom vystačili s použitím jediného způsobu vzniku pole a to numpy.full(count,fill_value).
Protože knihovna numpy byla motivována snadným psaním kódu, obsahuje mnoho dalších způsobů, jak můžeme vytvořit pole. I my tak potkáme ještě několik dalších možností. Zkusíme v našem kursu vystačit se dvěma cestami, jak vytvořit pole s jedním indexem.
Vytvoříme pole o dané délce vyplněné předepsanými hodnotami
Již víme, že
numpy.full(count, fill_value)vytvoří pole naplněné prvky téže hodnoty a tedy i téhož typu. Hodnoty pole pak budeme podle potřeby modifikovat, typ hodnot v průběhu doby existence pole změnit nejde.Zkratka
numpy.zeros(n)je pohodlnější a rychlejší ekvivalentnumpy.full(n,0.0). Tuto variantu vytvoření pole daných rozměrů budeme užívat nejčastěji.Funkce
numpy.linspace(a,b,num)vrátí pole čísel rovnoměrně pokrývající interval \(<\!\!a,b\!\!>\). Viz též kód funkcemy_linspaceníže. TODO:REF
Vytvoříme pole o hodnotách a délce daných jinými daty, obvykle provedením konverze typu. (Pozor: z historických důvodů nemá tato konverze tvar
nazev_typu(puvodni_data), kde název typu by měl býtnumpy.ndarray.)Velmi užitečné je určit hodnoty výčtem, např.
numpy.array([x0,x1,x2,x3,...])vytvoří pole o tolika prvcích, kolik jich je v hranatých závorkách uvedeno a o hodnotách, jaké v závorce uvedeme. Jde o konverzi hodnoty[x0,x1,x2,x3,...], která, jak víme, je typulist.Pokud bychom odhad společného typu nahradili pro jednoduchost operací
sum(která dává smysl jen pro číselné typy), mohli bychom takovou konverzinumpy.array(lst)připodobnit funkcí založenou nanp.fullPython def list2array(lst): """konverze 1-d seznamu na pole numpy.""" n = len(lst) val = sum(lst) array = np.full(n,val) for i in range(n): arr[i] = lst[i] return arrJiž jsme viděli, že
rangepředstavuje návod na procházení intervalu celočíselné aritmetické řady. I na něj lze aplikovat konverzi, tedy např. psátnumpy.array( range(1,7) ). Tím získáme totéž, jako zápisemnumpy.array([1,2,3,4,5,6]).Do této kategorie spadá i důležité vytvoření duplikátu pole, tedy
y = x.copy(). Brzy uvidíme, proč potřebujeme takové duplikáty. Samozřejmě, i zde bychom vystačili s aplikacínp.full, např.Python def array_copy(old_array): """Vytvoření kopie 1-d pole numpy.""" n = len(old_array) new_array = np.full(n,arr[0]) for i in range(n): new_array[i] = old_array[i] return new_array
Obě cesty obsahují nástrahu: numpy.full(4,1) vytvoří stejné pole jako numpy.array([1,1,1,1]). Jde o čtveřici celých nikoli reálných čísel. Pokud tedy jako hodnotu prvků v numpy.full uvedeme celé číslo nebo ve výčtu numpy.array([...]) uvedeme samá celá čísla, nemusí se chování pole shodovat s vašimi představami obvykle založenými na vlastnostech reálných čísel. To proto, že přiřazením do prvku pole nemůžeme změnit společný typ všech hodnot pole. Operací s celým pole to ale
samozřejmě půjde. Připomeňme, že jistou míru bezpečí před tímto druhem chyby představuje funkce numpy.zeros(n) ekvivalentní numpy.full(n,0.0).
Neplatné hodnoty indexů polí (IndexError)
Především, pokud mluvíme o polích poskytovaných knihovnou numpy, jejich indexy by měly být celá čísla (případně další od nich odvozené složitější konstrukce). Pokud tedy omylem zatoužíme po prvním prvku pole a místo indexu 0 použijeme reálné číslo 0.0, dočkáme se chybového hlášení, které nám to připomene (text chybového hlášení je zkrácen)
IndexError: only integers, slices (`:`), ... and integer or boolean arrays are valid indices
Jiná chyba nastane, pokud použijeme hodnotu celého čísla, která je za hranicemi pole. V tom případě je nám jeho délka v chybovém hlášení připomenuta
IndexError: index 20 is out of bounds for axis 0 with size 20
U matic hlášení sdělí, zda jsme špatně zadali index řádku (axis 0) nebo index sloupce (axis 1).
Otázka: Jak to, že když má pole podle chybového hlášení výše velikost \(20\), vede index o hodnotě \(20\) k chybě?
Záporné indexy
Již víme, že s[0] je první prvek pole/seznamu. Pokud bychom napsali s[-1] znamenalo by to v jazycích, jako je např. C, pokus zjistit hodnotu nacházející se v paměti počítače těsně před prvním prvkem pole. Obvykle je to nezamýšlená, chybná operace a podle situace vede okamžitě nebo po chvíli k ukončení běhu programu (lepší situace) nebo ke špatnému výsledku výpočtu.
V Pythonu jsou záporné indexy použity ve významu indexování od konce pole/seznamu, takže použití s[-1] znamená poslední prvek pole, s[-2] je ten předposlední atp.
Přiřazovací příkaz s poli
U polí se silně projeví důležitá vlastnost přiřazovacího příkazu a povaha proměnných v jazyce Python. Jde o to, že * Proměnné Pythonu představují štítky s odkazy na aktuální data * Přiřazením do proměnné měníme odkaz, ne hodnotu dat! * Na tatáž data tak může odkazovat více proměnných * U polí lze změnit nejen na co proměnná odkazuje, ale také hodnoty jednotlivých prvků, např. a[1]=4. Tím se ale mění hodnota druhého prvku pole odkazovaného proměnnou a, ale i všech dalších
proměnných, které na toto pole odkazují. Jde o zamýšlenou vlastnost jazyka Python, který dokonce zavádí kategorii mutable (pozměnitelných) typů. Doposud nám nevadilo, že hodnota na hodnotu \(4\) odkazují všechny proměnné, které přiřazením získaly tuto hodnotu. To proto, že onu čtyřku není možno nijak pozměnit, provedením operace, např. a=a+1 začne proměnná a odkazovat na pětku aniž se na čtyřce něco změní. Celá čísla (typu int) jsou *immutable**.
Uvažte kód
import numpy as np
a = np.full(3,1.0)
b = a
a[1] = 4
b[2] = 9
print(a, b)
Rozmyslete si nejprve, co očekáváte za výstup. Poté kód spusťte a zjistěte, zda splňuje vaše očekávání. Pokud ne, vraťte se k záhlaví "Přiřazovací příkaz s poli".
Rada:
Místo přiřazení
nove_pole = stare_pole
automaticky používejte tvar
nove_pole = stare_pole.copy()
Málokdy v našem kurzu totiž potřebujeme dvě proměnné odkazující pod různými jmény na totéž pole. (Tento postup, nefunguje pro seznamy seznamů, např. [[1,2],[3,4]], nicméně typ list je v našem kurzu v nemilosti, takže to můžeme opomenout a používat metodu copy() k získání duplikátu vektorů i matic.)
Na toto chování polí při přiřazení musíme pamatovat také, když předáváme funkci argument typu pole a tento uvnitř funkce měníme. Předání argumentu lze chápat jako přiřazení a uvnitř funkce tak původní pole vystupuje pod novým jménem, ale jde o tatáž data, a většinou proměnnou, která představovala při volání funkce její argument, měnit nechceme.
Další elementární operace s poli
POčet prvků (délku) pole zjistíme (mimo jiné) výrazem len(s). Proto, kdybychom se to nenaučili za chvíli jednodušeji, s[len(s)-1] je poslední prvek seznamu.
Ačkoli je neefektivní připojovat k seznamu uloženému v numpy.ndarray další hodnoty, pokud to potřebujeme máme k dispozici operaci promenna_typu_pole.resize(nova_velikost).
Typy prvků polí v numpy
Popularita této knihovny je také dána tím, že její správné použití přinese podstatné urychlení oproti zabudovanému typu list. Toho je dosaženo dvěma kroky - Všechny prvky pole jsou stejného typu - S tímto typem umí procesor efektivně pracovat
První vlastnost má důležité důsledky při vytváření polí z jiných hodnot. Pokud použijeme konverzi ze seznamu hodnot různého typu, společný typ se odvodí z nejširšího typu z následující řady int<float<complex<string<..., jaký se nalezne mezi konvertovanými hodnotami . Proto numpy.array([1,2,3]) vytvoří pole celých čísel, zatímco numpy.array([1,2,3.0]) vytvoří pole čísel reálných.
Celá čísla v numpy
S celými čísly je v programování potíž, protože jejich zápis sice vyžaduje konečný počet cifer, ale ne nezbytně počet malý. Python zvládá tuto potíž skrývat, i pokud je výsledek operace velmi dlouhé číslo. I tak se tato potíž může projevit, viz např. chybové hlášení pro příkaz print(math.factorial(2000)).
Aby mohl počítač s celými čísly efektivně pracovat musejí být interně uložena v dvojkovém tvaru. (Rozmyslete a vyzkoušejte si, že číslo dvacet má dvojkový zápis \(10100_2\), např. příkazem print(0b10100).) Počet bitů celého čísla se kterým procesor pracuje naráz navíc souvisí s počtem vodičů, jimiž se dopravují data uvnitř výpočetní jednotky procesorů. Shrnuto, dnešní počítače pracují efektivně s celými čísly o délce 8,16,32 a 64 bitů. To představuje následující intervaly, v kterých celé
číslo o takové bitové šířce může ležet:
[ ]:
for n in [8,16,32,64]:
print(f'{n:2}-bitové celé číslo bez znaménka: 0..{2**n-1:<30}')
print(f' se znaménkem: {-2**(n-1)}..{2**(n-1)-1}')
8-bitové celé číslo bez znaménka: 0..255
se znaménkem: -128..127
16-bitové celé číslo bez znaménka: 0..65535
se znaménkem: -32768..32767
32-bitové celé číslo bez znaménka: 0..4294967295
se znaménkem: -2147483648..2147483647
64-bitové celé číslo bez znaménka: 0..18446744073709551615
se znaménkem: -9223372036854775808..9223372036854775807
Funkce a pole
Musíme nyní diskutovat, jak psát funkce, které pracují s poli. Máme tu několik rolí, ve kterých tato pole mohou vystupovat:
Vstupní argument, jehož hodnotu uvnitř funkce neměníme.
Vstupní argument, jehož hodnotu uvnitř funkce měníme, ale nechceme aby to bylo "vidět venku".
Vstupně-výstupní argument, který měníme a chceme, aby to bylo vidět venku
Výstupní hodnota (např. funkce
geom_posloupnost(a0,q,n)může vracet n členů g. posloupnosti).Globální proměnná může vystupovat (někdy i zároveň) v obou výše uvedených rolích.
Argumenty typu pole - vstupní argument (jen pro čtení)
Začneme funkcí, která spočte součet kladných prvků seznamu/pole. Níže uvedený kód řeší následující otázky:
jaký je první a poslední index prvku pole
zda je prvek kladný
nulování, přičítání a navrácení součtu
[ ]:
def sum_positive(a):
""""Součet kladných prvků seznamu"""
soucet = 0
for i in range(len(a)):
if a[i]>0:
soucet = soucet + a[i]
return soucet
pole = np.array([-2,-1,0,1,2])
print( 'sum =',sum_positive( pole ) )
sum = 3
Tento kód se záměrně podobá tomu, jak bychom je psali např. v C, tedy zejména používá indexy. Modernější přístup využije toho, že for umí procházet přímo prvky pole:
[ ]:
def sum_positive_v2(a):
""""Součet kladných prvků seznamu"""
soucet = 0
for x in a:
if x>0:
soucet = soucet + x
return soucet
pole = np.array([-2,-1,0,1,2])
print( 'sum =',sum_positive_v2( pole ) )
sum = 3
Vidíme, že obě verze nemění hodnotu argumentu a.
Ne všechny funkce, které mají za vstup pole budeme muset psát. Existuje např. funkce sum, která počítá součet prvků pole. Využijeme toho k dalšímu výkladu.
Uvažujme následující variantu funkce sčítající pozitivní členy pole:
[ ]:
def sum_positive_v3(a):
""""Součet kladných prvků seznamu"""
for i in range(len(a)):
if a[i]<0:
a[i] = 0
return sum(a)
pole = np.array([-2,-1,0,1,2])
print( 'sum =',sum_positive_v3( pole ) )
print( 'pole =', pole )
sum = 3
pole = [0 0 0 1 2]
Zde se projevily vedlejší účinky volání takové funkce: proměnná, kterou dostala jako argument byla pozměněna.
Cvičení: Opravte funkci sum_positive_v3 tak, aby neměnila hodnotu proměnné, která je jí předána jako argument. (Využije např. metodu copy().)
Volání funkcí s argumentem typu pole
Volání funkce sum_positive výše se podobá např. volání funkce abs, u které můžeme např. psát abs(x), abs(-5), abs(x-y). Můžeme tedy - Předat funkci jako argument proměnnou sum_positive(x) - Předat funkci jako argument výraz - něco jako konstantu sum_positive(np.array[(-1,1,2)]) - nebo výraz sum_positive(-x) (uvidíme, že \(-\{a_k\} = \{-a_k\}\)) - ještě složitější výraz ...
Dobrým důvodem pro předávání polí funkci je např., pokud z nich tato funkce dokáže namalovat obrázek.
Malování obrázků (knihovna matplotlib)
Jednou z velmi pohodlných vlastností Pythonu je, že máme k dispozici i knihovnu pro malování jednoduchých obrázků. Seznámíme se s ní zde, protože pole hrají roli vstupních argumentů těchto funkcí určujících např. souřadnice malovaných bodů a čar.
Grafy funkcí kreslíme za pomoci funkce plot z knihovny matplotlib.pyplot. Z rozsáhlého seznamu možností zvolíme jen naprosté minimum, zbytek naleznete v dokumentaci
Pozn. Až na řádek, kde otáčíme najednou znaménko všech prvků pole zápisem -body_y, pokud víte jak, můžete v kódu použít pro data jednodušší typ list.
[ ]:
import matplotlib.pyplot as plt
body_x = np.array( [0,1,2,3,4,5] )
body_y = np.array( [4,-3,2,-2,3,-4] )
plt.plot( body_x, body_y )
plt.plot( body_x, -body_y, ':' )
plt.title("plt.plot( body_x, body_y )")
plt.show()
plt.plot( body_x, body_y, 'o-r' )
plt.title("plt.plot( body_x, body_y, 'o-r' )")
plt.show()
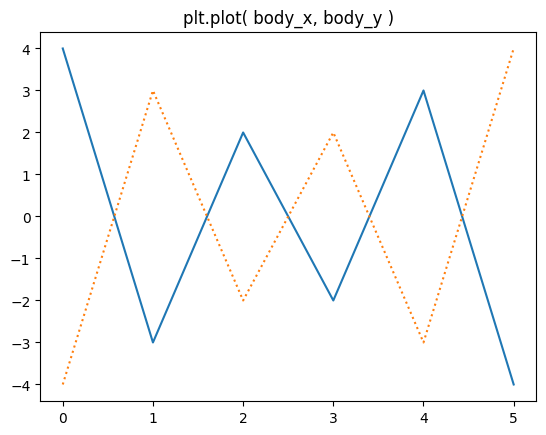
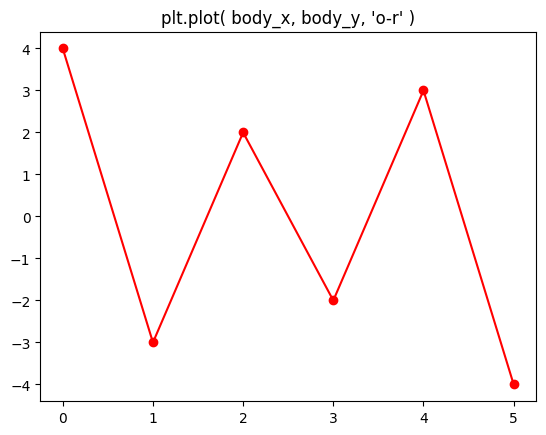
Dokumentace funkce plot je rozsáhlá, zmiňme jen, že první a druhý argument jsou pole x-ových a y-ových souřadnic bodů. Pokud neuvedeme další argumenty, vykreslí plot lomenou čáru. Další argument umožňuje modifikovat styl barvu atd, např. ':' je tečkovaná a '--' čárkovaná čára, zatímco 'o-r' je plná čára ('-') spojující puntíky ('o') obojí v červené barvě ('r'), atp.
Občas ještě budeme potřebovat funkci scatter pro malování puntíků různých velikostí a barev.
[3]:
import matplotlib.pyplot as plt
body_x = np.array( [0,1,2,3,4,5] )
body_y = np.array( [4,-3,2,-2,3,-4] )
plochy = np.array( [10,100,300,500,300,100] )
barvy = np.array( ['r','g','b','c','m','y'] )
plt.scatter( body_x, body_y, s=plochy, c=barvy )
plt.title("plt.scatter( ... )")
plt.show()
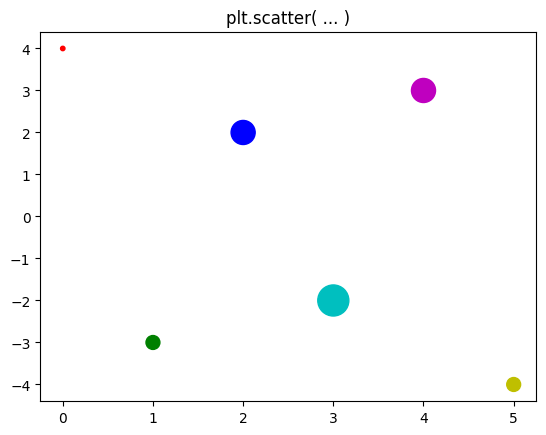
Argumenty typu pole - výstup
Protože jsou argumenty v Pythonu předávány jako odkazy, můžeme je někdy měnit. Má to ale své podmínky:
argument musí být mutable typu (to pole splňují)
nesmíme použít přiřazení do proměnné ale jen do její části
můžeme také používat metody, jako je třeba
appendu typulist
Nejprve si ilustrujeme správný postup:
[17]:
def vynuluj_zaporne(a):
for i in range(len(a)):
if a[i]<0:
a[i] = 0
pole1 = np.array( [1,-1,2,-2,3,-3,4] )
vynuluj_zaporne(pole1)
print(pole1)
[1 0 2 0 3 0 4]
Nyní totéž špatně. Následující funkce nemodifikuje jednotlivé prvky pozměňováním a[i] postupně pro všechna i. Místo toho spočte správný výsledek najednou na základě vlastností funkce \((x+|x|)/2\) a tento dosadí do a.
[ ]:
def vynuluj_zaporne_spatne(a):
print('hodnota a na zacatku',a)
a = (a+np.abs(a))/2
print('hodnota a na konci ',a)
pole1 = np.array( [1,-1,2,-2,3,-3,4] )
vynuluj_zaporne_spatne(pole1)
print(pole1)
hodnota a na zacatku [ 1 -1 2 -2 3 -3 4]
hodnota a na konci [1. 0. 2. 0. 3. 0. 4.]
[ 1 -1 2 -2 3 -3 4]
Vidíme, že pole1 zůstane nezměněno, ačkoli argument a po aplikaci vzorce nabyl uvnitř funkce správných hodnot.
Klíčovou chybou je začátek příkazu
a = ...
Podstata přiřazovacího příkazu v jazyce Python totiž určuje, že tím změníme, na co lokální symbol a ukazuje, nikoli vlastní hodnoty na které před přiřazením a odkazovalo. Od tohoto okamžiku tedy máme původní pole1 se zápornými čísly a pak nová data na která odkazuje proměnná a. Tato data jsou lokální v dané funkci na jejím konci zmizí, zatímco pole1 se nezmění.
Časem se dovíme, že v problém lze řešit též použitím tzv. řezů a[:] = ..., kdy přepíšeme najednou více prvků pole, aniž by a začalo odkazovat na jiné pole. Spíše ale v takovéto situaci je správné použít příkaz return.
Takové funkce buď pole vytvoří nebo spočtou jako modifikaci pole vstupního a pak použijí příkaz return. Například
return (a+np.abs(a))/2
Jako ukázku si napíšeme funkci, která počítá tabulku funkčních hodnot \(f(x_i)\) pro \(x_i\) rovnoměrně pokrývající interval \(<\!\!a,b\!\!>\). Argumenty funkce budou čtyři: funkce f, meze intervalu a,b a počet bodů pokrývajících tento interval ve kterých se má funkční hodnota spočíst.
Všimněte si, že funkce function_table má pole jako svůj výstup, zatímco plot zase jako vstup a že je možné tyto role propojit.
Pozn. Časem totéž dosáhneme s použitím numpy.linspace.
[ ]:
def function_table(f, start, end, count=400):
tab = np.full(count, 0.0)
for k in range(count):
x = start + (end-start)*k/(count-1)
tab[k] = f(x)
return tab
from math import sin,cos,pi
import matplotlib.pyplot as plt
p,q = 4,7
plt.plot( function_table(sin,0,p*2*pi), function_table(cos,0,q*2*pi) )
plt.show()
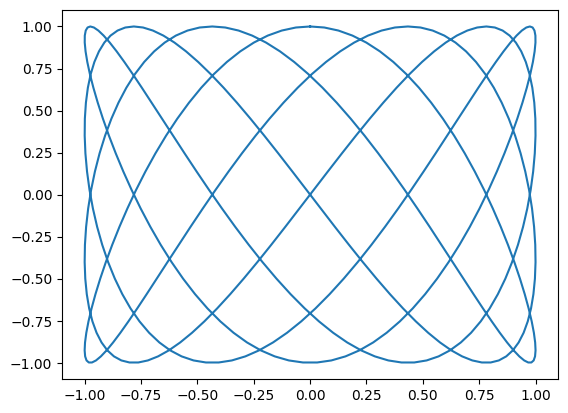
Protože Python stejně pracuje s odkazy, není vracení polí nic speciálního. Uvědomme si však proč by to mohl být problém. Pokud funkce vrací pole, například náhodných čísel, pak v příkazu
print( sum_positive( seznam_nahodnych_cisel(1_000_000) ) )
musí někde chvíli existovat seznam milionu čísel a to od chvíle, kdy je vytvořen až do okamžiku, kdy skončí sčítání. Poté ale již seznam není potřeba a protože milion čísel není málo, je potřeba uvolnit paměť, kterou zabíral. Věc by se ještě mohla zkomplikovat tím, kdyby si (například za účelem ladění) funkce sum_positive poznamenala odkaz na poslední sčítané pole. Potom by úklid milionu prvků nastal až po dalším zavolání této funkce, protože ta by si při něm poznamenala odkaz na nové pole,
čímž by ten starý přestal existovat.
Právě neviditelnost těchto operací určuje mnohé vlastnosti a asi i popularitu jazyka Python a odlišuje jej např. od C, kde tohle musíme explicitně řešit. Cenou, kterou za pohodlí platíme bývá m.j. rychlost.
Jednou z možností, jak organizovat práci s poli je mít je uložené v jedné nebo několika globálních proměnných.
Program pak sestává z procedur, která s těmito daty vhodně manipulují. Nemusejí ale typicky řešit jejich předávání - data celou dobu sídlí v k tomu určených proměnných.
Uvažujme následující jednoduchý příklad programu.
Hlavní program
inicializuje tabulku prvočísel prostřednictvím volání funkce
eratosthenesvyrobí tabulky hodnot, přičemž použije opakovaně funkci
goldbach_countnamaluje obrázek
Podprogramy
funkce
eratosthenesobsadí globální proměnnou pojmenovanouje_prvocislo. Protože do této proměnné přiřazeuje, je v ní uvozena jakoglobal je_prvocislofunkce
goldbach_countnamaluje spočte počet párů prvočísel dávajících daný součet. Proměnnouje_prvocislosilně používá ale nemodifikuje
Povšimněte si, že použití globální proměnné v kódu na rozdíl od mnoha jiných jazyků, nemusí předcházet řádku, kde je proměnná vytvořena. Vznik proměnné je totiž odlišný od deklarace, jaká se používá např. v C.
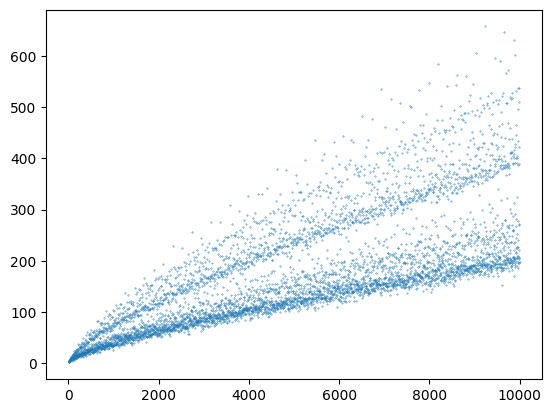
Pozn. Až se to naučíme, je goldbach_count dobře akcelerovatelná použitím @njit. (Ještě většího zrychlení výpočtu lze ovšem dosáhnout za použití nápadů slavných matematiků. Čtení o Goldbachově hypotéze.)
[ ]:
# Program počítá, kolik dvojic prvočísel dává daný součet (sudý a větší než 2)
# Souvisí s Golbachovu hypotézou, která říká, že se vždy nějaká dvojice najde
# Program demonstruje použití/sdílení globálních proměnných více funkcemi
# (a nikoli optimální algoritmus vykreslující "Goldbachovu kometu")
import numpy as np
import matplotlib.pyplot as plt
def goldbach_count(k):
"""Počet dvojic prvočísel dávajících v součtu hodnotu k.
Používá globální proměnnou je_prvocislo,
kterou vytvoří procedura erarosthenes."""
assert k%2==0 and k>2, "k musí být sudé a větší než 2"
p_max = len(je_prvocislo)-1
assert k<p_max, "Příliš krátký seznam prvočísel"
count = 0
for p in range(2,k-1):
if je_prvocislo[p] and je_prvocislo[k-p]:
count = count+1
return count
def eratosthenes(n):
"""Vytváří pole [False,False,True,True,False,True,...] délky n+1
indikující, že mezi čísly 0..n jsou 2,3,5,... prvočísla"""
global je_prvocislo
je_prvocislo = np.full(n+1, True)
je_prvocislo[0] = False
je_prvocislo[1] = False
p = 2
while p*p <= n:
if je_prvocislo[p]:
for nasobek_p in range(2*p,n+1,p):
je_prvocislo[nasobek_p] = False
p = p + 1
n_max = 10000
eratosthenes(n_max)
delka_pole = n_max//2-2
suda = np.full(delka_pole,0)
pocty = np.full(delka_pole,0)
for k in range(delka_pole):
s = 2*k+4 # cisla 4,6,8,....
suda[k] = s
pocty[k] = goldbach_count(s)
plt.scatter( suda, pocty,s=0.1)
plt.show()
Globální proměnná v roli statické lokální proměnné
Někdy musíme použít globální proměnnou i když s ní pracuje jen jedna jediná funkce a zasloužila by si tedy být proměnnou lokální. Mohli jsme to potkat již dříve, kdybychom psali funkci, která potřebuje uložit mezi svými voláními nějaký stav. I u numerického kódu je občas potřeba si pamatovat hodnoty mezi voláními funkce: někdy kvůli urychlení, jindy z principu. Často pak mají tyto hodnotu podobu polí.
Jednoduchým příkladem globální proměnné poskytující službu úschovny pro nějakou funkci je varianta funkce, která počítá obvod elipsy vzorečkem TODO:REF.
Hlavním bodem výpočtu je součet mocninné řady, přičemž koeficienty řady jsou dost složité na to, aby, když už je jednou spočteme, bylo výhodné si je uložit pro příště. Již dříve jsme použili jsme následující vzorec pro obvod elipsy s poloosami \(a,b\)
Nepředstavuje sice optimální návod na výpočet obvodu elipsy, ale umožní nám demonstrovat obvyklou možnosti zrychlení tohoto typu výpočtů. Sumu v závorce můžeme zapsat \(\sum_{k=1}^\infty a_k \epsilon^{2k}\), přičemž
Pokud bychom opakovaně potřebovali počítat obvody elips s různou výstředností, mohlo by být výhodné mít uschované hodnoty \(a_k\). (Lepší postup pro numerický výpočet obvodu elipsy najdete zde a je implementován v knihovně scipy, kterou použijeme pro kontrolu správnosti našeho výpočtu.)
[ ]:
import numpy as np
def obvod_elipsy(a, b, rtol=1e-10):
global oe_ak_ready
if b>a:
a,b = b,a
eps2 = 1-b**2/a**2
eps2k = eps2
atol = 0.5*rtol*(1-eps2)
s = 1
for k in range(1,oe_ak_ready+1):
ds = oe_ak[k]*eps2k
s -= ds
if ds<atol:
return 2*np.pi*a*s
eps2k *= eps2
for k in range(oe_ak_ready+1,oe_max_k):
oe_ak[k] = oe_ak[k-1]*(2*k-1)*(2*k-3)/(4*k*k)
oe_ak_ready = k
ds = oe_ak[k]*eps2k
s -= ds
if ds<atol:
return 2*np.pi*a*s
eps2k *= eps2
assert False, "Soucet rady nekonverguje"
oe_max_k = 1000
oe_ak = np.full(oe_max_k,0.25)
oe_ak_ready = 1
import scipy.special
def obvod_elipsy_presne(a, b):
""""Výpočet obvodu elipsy s použitím eliptických integrálů z knihovny scipy"""
eps2 = 1-b**2/a**2
return 4*a*scipy.special.ellipe(eps2) # zajímavost: funguje i pro eps2<0
rel_chyba = obvod_elipsy(1,0.2)/obvod_elipsy_presne(1,0.2) - 1
print(f'{rel_chyba = } {oe_ak_ready = }')
rel_chyba = 6.183942247162122e-11 oe_ak_ready = 331
Povšimněte si, že příkaz global oe_ak_ready se týká jen jedné ze třech globálních proměnných používaných funkcí obvod_elipsy. Již víme, že je to proto, že jen do této globální proměnné uvnitř funkce dosazujeme. Přitom modifikujeme i druhou proměnnou oe_ak, ve které postupně budujeme tabulku koeficientů. Je to ale jen přiřazení, před kterým jsou globální proměnné "ochráněny" existencí příkazu global!
Poznámka: Bývá zvykem, když vše, co funkce potřebuje interně ke svému provozu má podobu lokálních proměnných. Jejich existence je ale běžně omezena na dobu běhu funkce, zatímco zde potřebujeme, aby tabulka hodnot koeficientů existovala i mezi voláními funkce. Za tímto účelem například v jazyce C/C++ máme modifikátor static, kterým říkáme, že lokální proměnná má existovat pořád. Protože v Pythonu ale statické lokální proměnné neexistují, používají někteří programátoři jako náhražku
atributy funkce. Protože funkce existuje počínaje provedením příkazu def funkce(...), je možné jak uvnitř funkce, tak na globální úrovni použít zápis funkce.id_promenne. Hodnota uložená v tomto atributu existuje nezávisle na lokálních proměnných funkce.
Globální proměnná v roli konstanty
Většina programovacích jazyků zná koncept konstanty. Jde o veličinu, která má po dobu běhu programu neměnnou hodnotu. My si snadno představíme např. \(\pi\), ale v typickém programu bývá mnohem víc konstant. Pro kompilované jazyky přinášejí konstanty možnost urychlit běh kódu, triválně například v příkazu y = 2*pi*r provést násobení \(2*\pi\) již během překladu a nezdržovat s ním při vlastním výpočtu.
Python nezná konstanty. ( Dokonce i hodnotu math.pi můžete změnit. )
To ovšem nic nemění na tom, že některé veličiny v programu mají význam konstant. Pokud se taková 'koncepční' konstanta objevuje ve funkci, znamená to, že ji při každém zavolání funkce je potřeba vytvořit. To se projeví zejména, pokud je konstanta typu pole. To v principu může zdržovat a jako řešení tedy máme možnost nahradit ji proměnnou globální. V Pythonu je dokonce doporučováno takové proměnné zapisovat velkými písmeny, aby bylo čtenáři (případně i editoru vývojového prostředí, nikoli však interpretu jazyka Python) jasné, že jde o konstantu.
Nejprve jednoduchý příklad: počítáme objem mnohostěnu s danou délkou hrany a počtem stěn. Pravidelné mnohostěny mohou mít jen 4,6, 8, 12 a 20 stěn. Pro každý z nich použijeme známý objem mnohostěnu s jednotkovou hranou (např. u krychle je to 1) a ten vynásobíme třetí mocninou délky hrany. Dokonce i v Pythonu se pozná, že u verze 1 takové funkce vždy znovu a znovu inicializujeme tabulku objemů Platónských těles.
[ ]:
import numpy as np
def objem_mnohostenu_v1(n,a):
"""Počítá objem pravidelného mnohostěnu s n stěnami a délkou hrany a"""
tabulka = np.array([0,0,0,0, 0.117851130197757921, 0, 1.0, 0,
0.471404520791031683,0,0,0,7.66311896062463197,
0,0,0,0,0,0,0,2.18169499062491237])
objem1 = tabulka[n]
assert objem1 != 0, f"Pravidelný {n}-stěn neexistuje!"
return objem1 * a**3
def objem_mnohostenu_v2(n,a):
"""Počítá objem pravidelného mnohostěnu s n stěnami a délkou hrany a"""
objem1 = OBJEMY_MNOHOSTENU[n]
assert objem1 != 0, f"Pravidelný {n}-stěn neexistuje!"
return objem1 * a**3
OBJEMY_MNOHOSTENU = np.array([0,0,0,0, 0.117851130197757921, 0, 1.0, 0,
0.471404520791031683,0,0,0,7.66311896062463197,
0,0,0,0,0,0,0,2.18169499062491237])
%timeit objem_mnohostenu_v1(20,2)
%timeit objem_mnohostenu_v2(20,2)
6.22 us +- 2.34 us per loop (mean +- std. dev. of 7 runs, 100000 loops each)
928 ns +- 8.64 ns per loop (mean +- std. dev. of 7 runs, 1000000 loops each)
Podobná situace může nastat, když nějaká funkce má za úkol spočíst měřenou veličinu na základě kalibračních dat, která jsou známá v okamžiku psaní kódu. Pak lze příslušnou tabulku, řekněme závislost odporu termistoru na teplotě, uložit do globální proměnné typu pole. Protože v Pythonu neexistují konstanty, je později možné doplnit program o proceduru, která načte lepší kalibrační data např. ze souboru.
Numerická kvadratura
Kvadratura je historicky slovo označující výpočet hodnoty určitého integrálu. Obvykle se použije relace
Ukážeme si lichoběžníkové pravidlo, pro \(n+1\) bodů ležících ekvidistantně na intervalu \(<a,b>\)
Odvodíme si Simpsonovo/Keplerovo pravidlo, ale hlavně numerickou kvadraturu vezmeme jako příklad použití globálních "konstant".
K Simpsonovi: - Lichoběžník neumí správně integrovat ani kvadratické polynomy - lineární substituce umožní uvažovat jen interval <-1,1> - symetrické rozložení \(x_i\) a sudé \(w_i\) automaticky integruje správně všechny liché mocniny - uhodneme \(w_i=\{1/3,4/3,1/3\}\) jako váhy integrující správně 1 a \(x^2\) pro \(x_i=\{-1,0,1\}\).
Ke Gaussovi - Není důvod vyžadovat ekvidistantní pokrytí intervalu - víc stupňů volnosti, větší mocniny lze integrovat přesně
Následuje příklad programu, který počítá numerickou hodnotu integrálu \(\int_0^1\sqrt{1+x^3} dx\). Používá numerickou metodu, která používá seznam bodů, kde se vyčíslují hodnoty integrandu a seznam vah, jakými tyto hodnoty přispějí k hodnotě určitého integrálu. Seznam poloh i vah představují konstanty, které se nezměnily od dob C. F. Gausse.
Co si pamatovat:
Lichoběžníkové pravidlo je \(f(x_i)~.~[0.5,1,1,1,1,0.5]\) * dx
vědět, že je dost neefektivní
že ani Simpsonovo vylepšení $f(x_i).[1,4,2,4,2,4,1] * dx/3 není nic moc
vědět, že ekvidistantní vzorkování funkce je většinou naivní a že správné jméno je Gauss
Program níže ilustruje
"konstanty" v Pythonu
defaultní parametry
naivní určení chyby porovnáním hrubého a jemného kroku
[ ]:
import numpy as np
GAUSS8 = np.array([
[0.183434642495649805,0.525532409916328986,
0.796666477413626740,0.960289856497536232],
[0.181341891689180991,0.156853322938943644,
0.111190517226687235,0.0506142681451881296]])
GAUSS16 = np.array([
[0.0950125098376374,0.2816035507792589,0.4580167776572274,
0.6178762444026438,0.7554044083550030,0.8656312023878318,
0.9445750230732326,0.9894009349916499],
[0.09472530522753425,0.0913017075224618,0.08457825969750125,
0.07479799440828835,0.06231448562776695,0.0475792558412464,
0.03112676196932395,0.01357622970587705]])
TRAPEZOID6 = np.array([[0.2,0.6,1.0],[0.2,0.2,0.1]])
SIMPSON11 = np.array([[0.0, 0.2, 0.4, 0.6, 0.8, 1.0],
[1/15,1/15,2/15,1/15,2/15,1/30]])
# sorry, zde fejkujeme sudy počet zdvojeným výpočtem v nule, proto 1/15
def quadrature(f, a, b, method=GAUSS8):
k = (b+a)/2
l = (b-a)/2
s = 0
for i in range(len(method[0])):
s = s + ( f(k+l*method[0,i]) + f(k-l*method[0,i]) )*method[1,i]
return s*(b-a)
def print_integral(f, a, b, method=GAUSS8):
intf = quadrature(f, a, b, method=method)
mid = (a+b)/2
intf2 = quadrature(integrand, a, mid, method=method) + quadrature(integrand, mid, b, method=method)
ee = abs(intf - intf2)
print(f"{intf} +- {ee:7.2}")
def integrand(x):
return np.sqrt(1+x**3)
print_integral(integrand, 0, 1, method=TRAPEZOID6)
print_integral(integrand, 0, 1, method=SIMPSON11)
print_integral(integrand, 0, 1)
print_integral(integrand, 0, 1, method=GAUSS16)
1.1149921123536037 +- 0.0027
1.111445816918736 +- 2e-06
1.1114479705504803 +- 1.8e-11
1.1114479705325755 +- 2.2e-16
Cvičení: K úloze se vraťte později, až se naučíte používat "universální funkce" z knihovny numpy tak, aby funkce integrand používala np.sqrt a další operace, které dávají smysl nejen se skalárními hodnotami, ale i s vektory numpy.ndarray. Zkuste poté přepsat funkci quadrature za použití numpy. Použijte též funkci np.dot(a,b), která, pokud dostane jako argumentu stejně dlouhé vektory, spočte \(\sum_i a_i b_i\), takže kód lze zjednodušit až do podoby
return (b-a)*np.dot(..., method[1])
Elementární algoritmy pracující s poli
Na přednášce si vysvětlíme několik jednoduchých příkladů realizujících základní činnosti s poli.
Obsazování polí hodnotami
Asi nejzákladnějším problém je obsazení pole hodnotami určenými indexem. Například může jít o aritmetickou posloupnost v matematickém zápise \(x_j = a + j\; h\).
Již jsme zmínili, že téhož lze dosáhnout použitím funkce numpy.linspace(a,b,num), také existuje funkce numpy.arange([start,]stop[,step]), která ovšem nezahrne do pole hodnotu stop.
[ ]:
import numpy
print(f"{numpy.arange(1,2,0.1) = }")
print(f"{numpy.linspace(1,2,11) = }")
numpy.arange(1,2,0.1) = array([1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9])
numpy.linspace(1,2,11) = array([1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. ])
Tyto funkce jsou natolik užitečné, že si jejich přibližné varianty napíšeme jako názornou ukázku, jak vytvářet pole.
[ ]:
def my_arange(start, stop=None, step=1):
"""Return evenly spaced values within a given interval. See numpy.arange(...)"""
if stop==None:
stop = start
start = 0
num = int( (stop-start)/step )
if num<0:
num = 0
result = np.zeros(num)
for i in range(num):
result[i] = start + i*step
return result
def my_linspace(start, stop, num=50):
"""Return evenly spaced numbers over a specified interval. See numpy.linspace(...)"""
result = np.zeros(num)
for i in range(num):
result[i] = (start*(num-1-i) + i*stop)/(num-1)
return result
Ještě než si ukážeme pohodlnější postup, nutno zmínit, že běžnou operací je vytvoření nového pole aplikací funkce na každý prvek jiného pole.
[3]:
# Demonstrace y[i] = f(x[i])
import numpy as np
import matplotlib.pyplot as plt
# nejprve nějaká funkce jedné proměnné
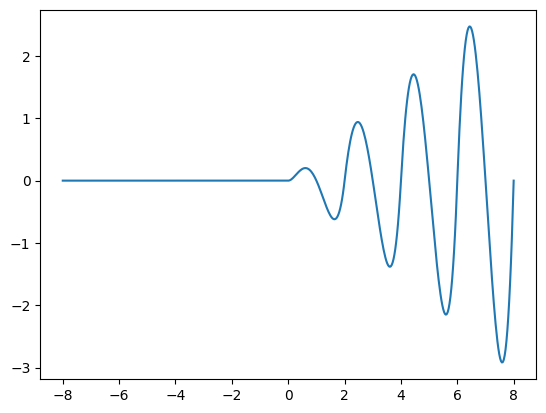
def funkce(x):
if x<0: return 0
t = x % 2.0
return x*t*(1-t)*(2-t)
# vytvoření hodnot x[i]
tabulka_x = np.linspace(-8,8,500)
# výpočet hodnot y[i] = f(x[i])
tabulka_y = np.zeros(len(tabulka_x)) # vytvoříme prázdné pole vhodné délky
for i in range(len(tabulka_x)):
tabulka_y[i] = funkce(tabulka_x[i])
# obrázek
plt.plot(tabulka_x,tabulka_y)
plt.show()
Univerzální funkce a výrazy s poli
Jakmile získáme rovnoměrně rozložené hodnoty pokrývající daný interval reálných čísel, můžeme využít schopností numpy sčítat, násobit a tp. celá pole a také spočíst hodnotu nějaké funkce pro všechny elementy pole "najednou".
V následujícím příkladě spočteme siny celých čísel do tisíce a pro zajímavost je i vykreslíme. Žargon označuje funkce, které lze aplikovat na všechny prvky pole najednou jak univerzální funkce. Můžeme tedy psát np.sin(pole) a získat najednou hodnoty sinů všech prvků pole.
Navíc můžeme používat operace +,-,*,/,**,//,% a zapisovat tak celé výrazy obsahující pole. Pokud sčítáme dvě pole p1+p2, musejí mít p1 a p2 stejnou délku, můžeme však také přičíst ke všem prvkům pole stejnou skalární hodnotu, tak že napíšeme p1+1. Podobně je o u dalších operací.
[15]:
p = np.linspace(0,4,5)
print(' p =',p) # pole
print(' 2*p =',2*p) # skalar*pole
print('4-2*p =',4-2*p) # skalar-skalar*pole
print(' ... =',np.sin(p)**2+np.cos(p)**2) # pole**2+pole**2
p = [0. 1. 2. 3. 4.]
2*p = [0. 2. 4. 6. 8.]
4-2*p = [ 4. 2. 0. -2. -4.]
... = [1. 1. 1. 1. 1.]
V následujícím příkladě využijeme toho, že np.sin vytvoří stejně dlouhé pole jako je jeho argument. Funkce pro malování totiž vyžaduje aby byl stejný počet x-ových a y-souřadnic malovaných bodů.
[20]:
# obsazení pole hodnotami danými funkcí
# příklad ufunc: np.sin
import numpy as np
import matplotlib.pyplot as plt
tabulka_int = np.arange(0,1000)
tabulka_sin = np.sin(tabulka_int)
plt.plot(tabulka_int,tabulka_sin,'.')
plt.show()
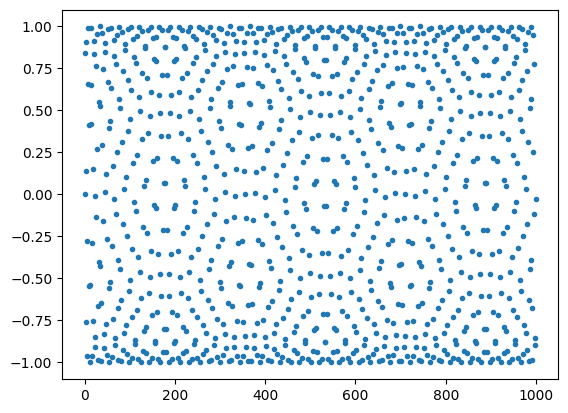
Úloha: Funkce \(\sin(x)\) má periodu \(2\pi\). Funkce \(\sin(\frac{\pi x}{\frac{22}{7}})\) má periodu \(2\times 22/7\). Vyzkoušejte, jak různé racionální aproximace ($3,:nbsphinx-math:frac{22}`7, :nbsphinx-math:frac{333}{106}`,... $) čísla \(\pi\) mění obrázek výše.
Vyhledávání v poli
Pole můžeme procházet nejen proto, abychom z něj spočetli pole jiné, ale také proto, abychom zjistili, zda se v něm daný prvek (zde číslo) nachází.
Napíšeme si funkci slow_in(x,a), která zjistí, zda se prvek x nachází v poli a. Jako obvykle v takové situaci, když prvek najdeme, může funkce okamžitě vrátit True a nemusí procházet zbylé prvky pole.
Funkci použijeme tak, že změříme čas, který potřebuje k nalezení posledního čísla v seznamu, a porovnáme to s rychlostí existující funkce volané v rámci testu x in a, jak jej nabízí jazyk Python a implementuje knihovna numpy.
[ ]:
# vyhledání prvku
def slow_in(x, a):
for y in a:
if y==x:
return True
return False
%timeit slow_in(999,tabulka_int)
%timeit 999 in tabulka_int
221 us +- 11.3 us per loop (mean +- std. dev. of 7 runs, 1000 loops each)
5.7 us +- 1.59 us per loop (mean +- std. dev. of 7 runs, 100000 loops each)
Opět vidíme, že funkce psané v Pythonu jsou oproti funkcím např. v C značně pomalejší, ale použití lepšího algoritmu to může dohnat. Pokud je totiž seznam setříděný, lze v něm vyhledávat pomocí "půlení intervalu".
Za pozornost v následujícím kódu stojí:
Vlastní algoritmus binárního hledání
Použití
//tedy celočíselného děleníPřiřazení
left=mid+1resp.right=mid-1která zaručí, že pokud prvek v seznamu není, skončíme nakonec sleft > righta tedy cykluswhilenemůže být nekonečný.
[ ]:
# binární vyhledání prvku v setříděném seznamu
def binary_in(x, a):
left = 0
right = len(a)-1
if x<a[left] or x>a[right]:
return False
while left <= right:
mid = (left+right)//2
if a[mid]==x:
return True
if a[mid]<x:
left = mid+1
else:
right = mid-1
return False
tabulka100k = np.arange(100_000)
%timeit binary_in(946,tabulka100k)
%timeit 946 in tabulka100k
18.4 us +- 5.45 us per loop (mean +- std. dev. of 7 runs, 10000 loops each)
56.3 us +- 9.79 us per loop (mean +- std. dev. of 7 runs, 10000 loops each)
Ověření vlastností hodnot uložených v poli
Následující dvě funkce ukazují, nejjednodušší příklady toho, jak projít seznam a prověřit nějakou jeho vlastnost. V prvním případě je to individuální vlastnost prvků, ve druhém pak vlastnost sousedních prvků v poli. Proto v druhém případě musíme použít indexy prvků, abychom sousedskost dokázali zapsat. V prvním případě nás zajímá jen hodnota jednotlivých prvků a tak indexy nepoužijeme (ale mohli bychom).
[ ]:
def all_positive(a):
"""Jsou všechny prvky seznamu a kladné?"""
for x in a:
if not x>0:
return False
return True
print( all_positive(tabulka_sin) )
print( all_positive(tabulka_sin+1) )
False
True
[ ]:
def is_sorted(a):
"""Představuje seznam a neklesající posloupnost?"""
for i in range(1,len(a)):
if not a[i-1] <= a[i]:
return False
return True
print( is_sorted(tabulka_int) )
print( is_sorted(tabulka_sin) )
True
False
Hledání optimálního prvku seznamu
Důležitou třídou problémů je hledání optimálního prvku seznamu. Obvykle procházíme prvek po prvku a kontrolujeme, zda není aktuální prvek lepší než ten nejlepší, co jsme doposud potkali. (Název funkce odráží fakt, že existuje funkce max.)
[ ]:
def slow_max(a):
wrk = a[0]
for x in a:
if x > wrk:
wrk = x
return wrk
slow_max(tabulka_sin)
0.999990471552965
Hledání optimálního prvku seznamu s podmínkou
V následujícím kódu řešíme kromě běžného procházení všech prvků pole také to, že žádný prvek nemusí splňovat požadovaná kritéria. Tento případ funkce musí nějak signalizovat. Využíváme toho, že Python poskytuje typ/hodnotu None.
Hodnotu None ale nemůžeme porovnávat a tedy podmínka aktualizace doposud nalezené optimální hodnoty musí obsahovat dvě podmínky. Aktualizace nastane jednak když wrk is None a nebo když x > wrk. Připomeňme si, že díky zkrácenému vyhodnocování logických výrazů nenastane chyba, protože, když je první podmínka splněna, or se neobtěžuje s vyhodnocováním druhé.
[ ]:
def max_negative(a):
wrk = None
for x in a:
if x < 0:
if wrk is None or x > wrk:
wrk = x
return wrk
max_negative(tabulka_sin)
-3.014435335948845e-05
Ještě následuje kód, který připomíná, že na to, abychom našli dva největší prvky pole, nemusíme nezbytně pole třídit.
[ ]:
def max2(a):
assert len(a)>1
m1 = a[0]
m2 = a[1]
if m1<m2:
m1,m2 = m2,m1
for i in range(2,len(a)):
x = a[i]
if x > m1:
m2 = m1
m1 = x
elif x>m2:
m2 = x
return m1,m2
max2(tabulka_sin)
(0.999990471552965, 0.9999900726865629)
Jedno pole, dva cykly
Zde si ukážeme příklady algoritmů, které nevystačí s jediným cyklem. (Ještě uvidíme, že často existují algoritmy rychlejší.)
Začneme hledáním duplicit.
[ ]:
def bez_duplicit(a):
n = len(a)
for i in range(1,n):
for j in range(i):
if a[i]==a[j]:
return False
return True
[ bez_duplicit(tabulka_int), bez_duplicit(tabulka_int%999) ]
[True, False]
Nadšenci do jazyka Python by možná navrhli mnohem (>30x) rychlejší realizaci téhož postupu. Například můžeme využít možnosti porovnávat celé pole s nějakou hodnotou, získat pole booleovských hodnot True/False a pak spočíst, kolikrát se ve výsledku objeví True, tedy kolik prvků tuto podmínku splňuje.
[ ]:
def bez_duplicit2(a):
for x in a:
if np.count_nonzero( a == x ) > 1:
return False
return True
[ bez_duplicit2(tabulka_int), bez_duplicit2(tabulka_int%999) ]
[True, False]
Takovýto postup je již za hranicemi toho, co v našem kurzu stihneme. Musíme vystačit jen s několika málo operacemi, jejichž kombinací dokážeme napsat programy realizující běžné algoritmy. Přesto výše uvedené urychlení výpočtu obsahuje jednu samozřejmou myšlenku, kterou musíme zmínit. Obvykle je to nejvnitřnější cyklus, který nejvíce ovlivňuje rychlost složitějšího výpočtu. Proto má smysl hledat optimální podobu kódu nejdříve tady. Navržený postup zdánlivě vnitřní cyklus odstraní, je to ale jen
proto, že několik cyklů je schovaných uvnitř operace == a funkce numpy.count_nonzero. Zrychlení hledání duplicit tedy nesouvisí s tím, že bychom vnitřní cyklus odstranili, ale s tím, že je zapsán v jazyce C.
K hledání duplicit v seznamu se ještě vrátíme, protože algoritmus výše není většinou optimální a budeme rozvažovat jaké jsou alternativy.
Následující příklady budeme podrobněji diskutovat v kapitole o složitosti, protože v našem začátečnickém kurzu se jednak učíme napsat správný kód (a to první varianta bez_duplicit splňuje) ale také si časem povíme, jak teoreticky posuzovat rychlost algoritmů, abychom mohli vybrat ten lepší. Z tohoto pohledu uvidíme, že bez_duplicit a bez_duplicit2 mají stejnou asymptotickou složitost \(O(N^2)\). A jako aplikaci takového teoretického rozvažování si ukážeme, že pro dlouhé seznamy
je lepší pole před hledání duplicit setřídit, protože duplicitu pak můžeme odhalit porovnáním sousedních prvků.
Tak jako jsme výše potkali neprobíranou část knihovny numpy i vlastní jazyk Python obsahuje části, které neprobíráme.
Zmiňme proto, že jeden možný test duplicit je založen na datové struktuře Pythonu - množině (set). Množina z principu daný prvek obsahuje nebo ne, nemůže tam ale být vícekrát. Proto konverzí set(pole) získáme množinu, jejíž počet prvků lze pak porovnat s počtem prvků původního pole. Kód je pozoruhodný svojí jednoduchostí a můžeme otestovat, že je i rychlý.
[ ]:
def bez_duplicit3(a):
return len(set(a)) == len(a)
[ bez_duplicit3(tabulka_int), bez_duplicit3(tabulka_int%999) ]
[True, False]
Pochopíme, že je výhodné hledat duplicity v setříděném seznamu. Naučíme se i teoreticky spočíst, kolikrát zhruba je takový postup rychlejší a to i když započteme čas potřebný pro setřídění seznamu. Zde jen kód, protože je naprosto srozumitelný, teorie později...
[ ]:
def bez_duplicit4(a):
n = len(a)
a = sorted(a)
for i in range(1,n):
if a[i-1] == a[i]:
return False
return True
[ bez_duplicit4(tabulka_int), bez_duplicit4(tabulka_int+[33]) ]
[ ]:
from numba import njit
@njit
def bez_duplicit5(a):
n = len(a)
for i in range(1,n):
for j in range(i):
if a[i]==a[j]:
return False
return True
[ bez_duplicit5(tabulka_int), bez_duplicit5(tabulka_int+[33]) ]
[ ]:
%timeit bez_duplicit(tabulka_sin)
%timeit bez_duplicit2(tabulka_sin)
%timeit bez_duplicit3(tabulka_sin)
%timeit bez_duplicit4(tabulka_sin)
%timeit bez_duplicit5(tabulka_sin)
[ ]:
bez_duplicit([1,5,8,3,1,4,6])
Problém: Najděte v seznamu dvě čísla, pro která je jejich podíl co nejblíže dané hodnotě.
Opět použijeme dva cykly, chytřejší algoritmus pro tento umělý problém nestojí za vymýšlení. To že mluvíme o podílu znamená, že nesmíme dělit nulou a že dělení není komutativní, takže budeme mít oba cykly úplné. Proto přichází v úvahu, nepoužívat cykly přes indexy.
[ ]:
def nejblizsi_podil(a, q):
"""V seznamu a najde dva prvky které mají podíl co nejblíže q. Může jít 2x o tentýž prvek."""
best_x = a[0]
best_y = a[0]
best_q = 1
for y in a:
if y!=0:
for x in a:
xy = x/y
if abs(xy-q) < abs(best_q-q):
best_x = x
best_y = y
best_q = xy
return best_x, best_y, best_q
nejblizsi_podil(tabulka_sin, 0.3)
Úloha: Napište verzi s indexy, tedy for i in range(n)..., která navíc garantuje, že čitatel a jmenovatel budou jiné prvky pole.
Úloha: Přidejte podmínku, že jmenovatel musí být kladný.
Úloha: Napište variantu této nejblizsi_podil(a, seznam_citatelu, seznam_jmenovatelu), která bude hledat optimální podíl \(q\approx m/n\), kde \(m\) bude náležet do seznamu čitatelů a \(n\) do seznamu jmenovatelů.
Úloha: Napište funkci, která pro danou hodnotu odporu nalezne nejlepsi dvojici rezistorů z řady E6, tedy s hodnotami odporu \(1,1.5,2.2,3.3,4.7,6.8,10,15,22,33,47,68,100, ... 10^6 \Omega\) - spojených sériově - spojených paralelně nebo sériově
Zde se učíme psát funkce, které pracují s poli. Ještě si o seřazování seznamů podle velikosti budeme povídat, ale již nyní si můžeme představit jeden snadno pochopitelný (ovšem, jak uvidíme, neefektivní) postup:
Buble-sort
Pole procházíme od začátku na konec a kdykoli potkáme špatně seřazenou dvojici sousedních prvků pole, prohodíme je. Snadno si rozmyslíme, že toto procházení pole musíme opakovat, přičemž, protože největší prvek takto probublá na konec seznamu, v dalším procházení můžeme vždy jedno testování ušetřit.
[ ]:
def buble_sort_inplace(a):
"""procedura setřídí pole, které dostane jako parametr. Nic nevrací. Učíme se na ní práci s poli, jinak je buble sort na nic."""
n = len(a)
for i in range(n-1,0,-1):
for j in range(i):
if a[j]>a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
k_setrideni = tabulka_sin.copy()
buble_sort_inplace(k_setrideni)
print(is_sorted(tabulka_sin), is_sorted(k_setrideni))
False True
[ ]:
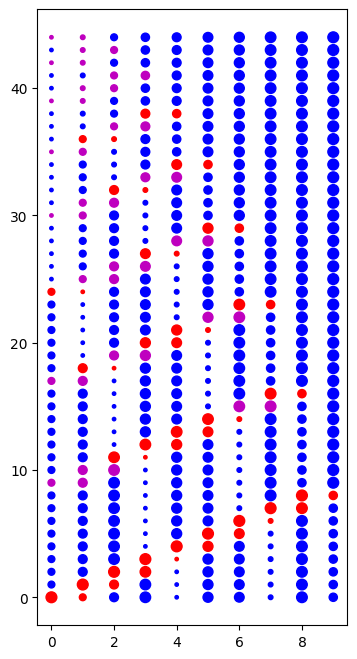
def buble_sort_demo(a):
"""Vytvoř obrázek ilustrující, jak bubble sort funguje. Používá vnořenou funkci, což se v našem kurzu neučíme."""
n = len(a)
# demo graphics
y = 0
demo_x = []
demo_y = []
demo_s = []
demo_c = []
def plot_row(color):
for k in range(n):
demo_x.append(k)
demo_y.append(y)
demo_c.append(color if k==j or k==j+1 else 'b')
demo_s.append(abs(a[k]))
for i in range(n-1,0,-1):
for j in range(i):
if a[j]>a[j+1]:
plot_row('r')
a[j], a[j+1] = a[j+1], a[j]
else:
plot_row('m')
y = y+1
import matplotlib.pyplot as plt
plt.figure(figsize=[4,8])
plt.scatter(demo_x,demo_y, c=demo_c, s=demo_s)
plt.show()
import math
k_setrideni = [int(abs(60*math.cos(20*k))) for k in range(0,10)]
buble_sort_demo(k_setrideni)
Řezy polí
Mimořádně užitečnou zkratkou pro práci s poli nebo maticemi jsou řezy. Nejprve si připomeňme funkci range. Používáme ji jako specifikaci hodnot, kterých má nabývat řídící proměnná cyklu. Pokud váháte, zopakujte si, co bude výstupem cyklu
for i in range(1,10,2):
print(i)
Seznamy i pole v Pythonu dovolují pracovat s více prvky pole najednou, pokud jako index pole uvedeme dvě nebo tři celočíselné výrazy oddělené dvojtečkou. Pokud uvedeme dvojtečku, ale nikoli hodnotu rozumí se hodnotou počátek (před první dvojtečkou) nebo konec pole (za první dojtečkou) nebo jednička (za druhou dvojtečkou).
Nejprve si ukažme, co znamená takový řez pole, pokud se objeví jako část výrazu. Například:
[8]:
pole = np.linspace(0,9,10)
print('pole = ',pole)
print('pole[ 1: 3] =',pole[1:3])
print('pole[ : 3] =',pole[:3])
print('pole[-3:-1] =',pole[-3:-1])
print('pole[-3: ] =',pole[-3:])
print('pole[ 1::2] =',pole[1::2])
pole = [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
pole[ 1: 3] = [1. 2.]
pole[ : 3] = [0. 1. 2.]
pole[-3:-1] = [7. 8.]
pole[-3: ] = [7. 8. 9.]
pole[ 1::2] = [1. 3. 5. 7. 9.]
V přiřazovacím příkaze mohou nastat dvě situace. - Do pole přiřazujeme pole stejného charakteru (počtu prvků) pole[0:4] = pole[10:18:2] - Do všech prvků vektoru přiřazujeme tutéž hodnotu pole[0:4] = 0
Užitečnost obsazení celého řezu pole jednou hodnotou potkáme již u Eratosthenova síta, kde proškrtávání násobků prvočísla p můžeme zapsat jedním přiřazením
if je_prvocislo[p]:
je_prvocislo[2*p:n+1:p] = False
Takový řez pole se může objevit všude, kde jsme zvyklí pracovat s polem, tedy například jako argument funkcí.
[16]:
phi = np.linspace(0,2*np.pi,129)
x = np.cos(phi)
y = np.sin(phi)
plt.axis("equal")
plt.plot(x,y)
plt.plot(x[::8],y[::8])
plt.plot(x[::16],y[::16])
plt.plot(x[::32],y[::32])
plt.show()

Úloha: Rozmyslete si, co dá výraz pole[::-1]+pole když jsme již výše vytvořili pole = np.linspace(0,9,10).
Pozor, v knihovně numpy jsou řezy chápány jako odkazy. Pokud tedy funkce argument typu pole mění, dojde ke změně původního pole.
Podobně se řezy polí mohou objevit na levé straně přiřazovacího příkazu. Zde je fakt, že měníme prvky daného pole zřejmý.
[22]:
zaporna_cisla = np.linspace(-10,-1,10)
print(zaporna_cisla)
vynuluj_zaporne(zaporna_cisla[::3])
print(zaporna_cisla)
zaporna_cisla[:3] = -11
print(zaporna_cisla)
[-10. -9. -8. -7. -6. -5. -4. -3. -2. -1.]
[ 0. -9. -8. 0. -6. -5. 0. -3. -2. 0.]
[-11. -11. -11. 0. -6. -5. 0. -3. -2. 0.]
Stěhujeme prvky pole
Součástí numerických algoritmů bývá i velmi nudná záležitost - stěhování polí a jejich částí. Protože to lze pokazit, musíme se o několika detailech zmínit.
Následující kód ilustruje - ztotožnění vektorů (ne nezbytně záměrné) - stěhování celých polí - stěhování částí polí - stěhování překrývajících se částí polí - špatně - dobře - pohodlně - varování: řezy polí (na rozdíl od seznamů) jsou odkazy, nikoli kopie
[55]:
def nove_pole(n=10):
global pole
pole = np.array(range(n))
print('ztotožení vektorů (ne nezbytně záměrné):')
nove_pole()
pole2=pole
pole2[1]=-1
print(pole,pole2)
print('stěhování celých polí:')
nove_pole()
pole2=pole.copy()
pole2[1]=-1
print(pole,pole2)
print('stěhování částí polí')
nove_pole()
pole[:3] = pole[-3:]
print(pole)
print('stěhování překrývajících se částí polí : špatně')
nove_pole()
for i in range(7):
pole[i+3] = pole[i]
print(pole)
print('stěhování překrývajících se částí polí : dobře')
nove_pole()
for i in range(6,-1,-1):
pole[i+3] = pole[i]
print(pole)
print('stěhování překrývajících se částí polí : pohodlně')
nove_pole()
pole[3:] = pole[:-3]
print(pole)
print('pozor, řezy polí jsou odkazy, nikoli kopie.')
nove_pole()
pole[0:5], pole[5:10] = pole[5:10], pole[0:5]
print(pole)
print('musíme tedy vtyrobit kopii !')
nove_pole()
pole[0:5], pole[5:10] = pole[5:10], pole[0:5].copy()
print(pole)
ztotožení vektorů (ne nezbytně záměrné):
[ 0 -1 2 3 4 5 6 7 8 9] [ 0 -1 2 3 4 5 6 7 8 9]
stěhování celých polí:
[0 1 2 3 4 5 6 7 8 9] [ 0 -1 2 3 4 5 6 7 8 9]
stěhování částí polí
[7 8 9 3 4 5 6 7 8 9]
stěhování překrývajících se částí polí : špatně
[0 1 2 0 1 2 0 1 2 0]
stěhování překrývajících se částí polí : dobře
[0 1 2 0 1 2 3 4 5 6]
stěhování překrývajících se částí polí : pohodlně
[0 1 2 0 1 2 3 4 5 6]
pozor, řezy polí jsou odkazy, nikoli kopie.
[5 6 7 8 9 5 6 7 8 9]
musíme tedy vtyrobit kopii !
[5 6 7 8 9 0 1 2 3 4]
Polynomy jako pole koeficientů
Snadno představitelnou aplikací polí různé délky je seznam koeficientů polynomu. Ze své definice má polynom \(\sum_{k=0}^n a_k x^k\) nějaký řád \(n\) a je tak určen koeficienty \(a_0,a_1,...,a_n\), volíme tedy, že seznam [-8,0,2] odpovídá polynomu \(2x^2-8\). Zde se hodí, že Python má indexy polí počínající nulou.
Pro nás je zajímavé, že běžné operace, jako je sčítání a násobení dvou polynomů opět vytvoří polynom. (U dělení bychom potřebovali pracovat s racionálními funkcemi.)
Pojďme si pár takových funkcí napsat jako procvičení práce s poli. Praktický význam je dost omezený, protože polynomy určené koeficienty jsou pro vyšší řády velmi náchylné k zaokrouhlovacích chybám.
Komentář k vybraným funkcím:
Ve funkci hodnota_polynomu(p,x) používáme Hornerovo schéma. Aby byl kód co nejpodobnější jiným jazykům, píšeme
p[n-1]místo v Pythonu dovolenéhop[-1].Sčítání polynomů musí brát v úvahu, že sčítané polynomy mohou mít různý řád. Příklady níže ukazují vybrané tři způsoby, jak to zohlednit.
Užitečné funkce pro práci s polynomy naleznete v části knihovny
numpy.polynomial.
[ ]:
def hodnota_polynomu(p,x):
"""Vrátí hodnotu p(x)"""
n = len(p)
f = p[n-1]
for k in range(n-2,-1,-1):
f = f*x+p[k]
return f
def soucet_polynomu(p,q):
lenp = len(p)
lenq = len(q)
r = np.zeros( max(lenp,lenq) )
for k in range(lenp):
r[k] = p[k]
for k in range(lenq):
r[k] += q[k]
return r
def soucet_polynomu_v2(p,q):
lenp = len(p)
lenq = len(q)
if lenp >= lenq:
r = p.copy()
for k in range(lenq):
r[k] += q[k]
else:
r = q.copy()
for k in range(lenp):
r[k] += p[k]
return r
def soucet_polynomu_v3(p,q):
lenp = len(p)
lenq = len(q)
r = np.zeros( max(lenp,lenq) )
r[:lenp] = p
r[:lenq] += q
return r
def soucet_polynomu_v4(p,q):
lenp = len(p)
lenq = len(q)
minpq = min(lenp,lenq)
r = np.zeros( max(lenp,lenq) )
r[:minpq] = p[:minpq]+q[:minpq]
if lenp>lenq:
r[lenq:] += p[lenq:]
elif lenq>lenp:
r[lenp:] += q[lenp:]
return r
p1 = np.array([1,2,3,4])
p2 = np.array([5,-2,11])
for f in [soucet_polynomu,soucet_polynomu_v2, soucet_polynomu_v3, soucet_polynomu_v4]:
p12 = f(p1,p2)
for x0 in range(11):
assert hodnota_polynomu(p12,x0) == hodnota_polynomu(p1,x0) + hodnota_polynomu(p2,x0)
Úloha: Napište funkci vracející součin dvou polynomů
Matice
Samozřejmě, pole mohou mít víc indexů. My si probereme několik příkladů, kdy půjde o pole, které má význam matice. Ty mají dva indexy, jeden vybírá řádek, druhý sloupec. Z výkladu bude jasné, jak postupovat, kdybychom potřebovali pole s více indexy.
Seznámíme se jen s následujícími operacemi a to jen pro pole s jedním a dvěma indexy:
vytvoření prázdného pole inicializovaného nulami
přístup k prvku pole
vytvoření kopie pole
řezy pole
aplikace funkcí a aritmetických operací na pole
se stejným počtem a rozsahem indexů
s jiným počtem indexů
numpy - vytvoření matice
Protože matice má obecně obdélníkový tvar, musíme zadat dvě dimenze. Ty je potřeba zadat jako seznam dvou celých čísel (pro znalé: místo seznamu by mělo jít o tuple, ale těm se v kurzu snažím vyhýbat).
matice_3x5 = np.zeros([3,5]) # 3 řádky, 5 sloupců
V základním kurzu budeme zjišťovat rozměry pole stejně jako u seznamu prostřednictvím funkce len (časem objevíte, že tvar pole je k dispozici v atributu shape, který je typu tuple).
Jak ale zjistit oba rozměry matice? Protože (zjednodušuji) se matice skládá z řádků, vrátí len(matice_3x5) hodnotu 3. Pokud si vybereme první řádek (index 0) a zjistíme jeho délku, tedy len(matice_3x5[0]), dostaneme počet sloupců: 5. Bereme první řádek, protože ten existuje i u matice dimenze 1 a matice mají všechny řádky stejně dlouhé.
[2]:
import numpy as np
p6 = np.zeros(6)
m3x5 = np.zeros([3,5])
print(p6)
print(type(p6), len(p6) )
print(m3x5)
print(type(m3x5), len(m3x5), len(m3x5[0]))
[0. 0. 0. 0. 0. 0.]
<class 'numpy.ndarray'> 6
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
<class 'numpy.ndarray'> 3 5
Následující funkce ilustrují jednoduchý způsob jak zjistit, co je dané pole zač.
Atribut shape vrací tuple. Počet položek, tj. len(a.shape) říká, kolik má pole indexů. Pro názornost ale místo použití shape zjišťujeme rozměry vektoru a matice níže za pomoci funkce len. (Kdo chce pracovat s typem tuple, jistě uhodne, jak v těchto funkcích nahradit funkci len atributem shape.)
[ ]:
import numpy as np
def is_ndarray(a):
return type(a) == np.ndarray
def is_numpy_vector(v):
if type(v) != np.ndarray:
return False
return len(v.shape) == 1
def is_numpy_matrix(m):
if type(m) != np.ndarray:
return False
return len(m.shape) == 2
def vector_dim(v):
return len(v)
def matrix_columns(m):
return len(m[0])
def matrix_rows(m):
return len(m)
[ is_ndarray(m3x3), is_numpy_vector(p6), is_numpy_vector(m3x3), is_numpy_matrix(m3x3), vector_dim(p6) ]
[True, True, False, True, 6]
Praktická rada: Povšimněte si, jak je psaná např. funkce is_numpy_matrix. Vzhledem k tomu, že na jejím druhém řádku nastane return pro všechny typy jiné, než numpy.ndarry, chytrá IDE, např. VScode, počínaje třetím řádkem 'vědí', jakého je m typu a nabídnou nám jeho atributy a metody při psaní kódu.
Cvičení: Napište všech 6 funkcí výše zpaměti. Jsou totiž důležité.
[ ]:
m42 = np.zeros([4,2])
print(m42)
[ matrix_rows(m42), matrix_columns(m42) ]
[[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]]
[4, 2]
Prvky matice
Matice má dva indexy, přičemž obvykle první udává řádek a druhý sloupec. Stále platí, že první index je 0. Máme-li tedy matici
vypadá tato v našem programu takto
a[0,0] a[0,1] a[0,2] a[0,3]
a[1,0] a[1,1] a[1,2] a[1,3]
a[2,0] a[2,1] a[2,2] a[2,3]
Pozn. Matice lze v principu vytvářet jako seznam seznamů. Pak ale musíme psát a[i][j]. Protože se ovšem kopie takovýchto matic vytvářejí jinak než kopie vektorů, dáme přednost numpy, kde je méně komplikací.
Následující funkce ilustruje vytváření matice.
[ ]:
# vytvoření jednotkové matice
# (samozřejmě, existuje np.eye, ale my se to teď učíme)
def matrix_1(dim):
a = np.zeros([dim,dim])
for i in range(dim):
a[i,i] = 1.0
return a
matrix_1(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
Cvičení: Napište funkci
def is_diagonal_matrix(m):
"""Vrátí False, pokud je některý z nediagonálních prvků matice nenulový."""
...
Cvičení: Napište funkci
def diagonal_matrix(d):
"""Funkce vytvoří nulovou matici n x n, kde n je dimenze vektoru určeného argumentem d a obsadí diagonálu prvky d"""
...
nahrazující np.diag(seznam_diag_prvku) stejným způsobem, jako matrix_1(3) napodobuje np.eye(3).
Příklad použití: diagonal_matrix([1,2,3]) musí vrátit
array([[1, 0, 0],
[0, 2, 0],
[0, 0, 3]])
Cvičení: Otestujte obě funkce.
Vytvoření kopie
Protože přiřazení ztotožňuje odkazy, musíme často vytvářet kopie. Pro numpy stačí na vektory i matice použít metodu copy, tedy
[ ]:
ma1 = np.zeros([2,2])
ma2 = ma1.copy()
ma3 = ma2
ma3[1,0] = 1000
print(ma1,"\n")
print(ma2,"\n")
print(ma3)
[[0. 0.]
[0. 0.]]
[[ 0. 0.]
[1000. 0.]]
[[ 0. 0.]
[1000. 0.]]
Řezy matic
Protože má matice dva indexy, můžeme řezy specifikovat několika způsoby.
a[i,:]představuje i-tý řádek maticea[:,i]představuje i-tý sloupec maticea[:2,:2]představuje levou horní 2x2 podmaticiatd
Opět můžeme do řezu maticí dosadit.
a[řez1,řez2] = maticea[řez1,řez2] = skalární_hodnotaa[řez1,řez2] = vektor_hodnota_kompatibilní_s_řez2
Pokud určíme pevně jeden z indexů máme na levé straně vektor a platí pravidla, která jsme zmiňovali u řezů s jedním indexem.
U matic musí v prvním případě navzájem souhlasit počet řádků a sloupců. Věš třetím případě proběhne přiřazení jednoho řádku do obdélníkové matice se stejnou délkou řádku. V dokumentaci numpy se o druhé a třetí variantě píše jako o rozšíření typu (broadcasting), kdy se skalár povýší na vektor, nebo matici, vektor na matici atp.
Univerzální funkce
Až na pohodlnější práci s maticemi jsme zatím nepotkali výrazný důvod, proč používat ndarray místo základního typu list.
Podívejte se ale na následující kód a povšimněte si jeho jednoduchosti.
[ ]:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0,10,800)
y = np.sin(30*x)+1.2*np.sin(31*x)
plt.plot(x,y)
plt.show()
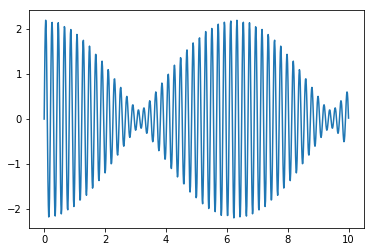
Stručně:
Funkce numpy.linspace pohodlně vytvoří 800 bodů rovnoměrně pokrývajících daný interval
numpy poskytuje m.j. funkci
np.sin, která spočte sinus pro všechny prvky pole, které dostane jako argument. Vrátí tedy stejně dlouhé pole, jako je argument.Další matematické funkce, které najdeme v
numpy:Funkce jedné proměnné: sqrt, cbrt, exp, log, log10, log2, log1p, real, imag, sin, cos, tan, arcsin, arccos, arctan, sinh, arcsinh, ...
Funkce dvou polí (prvek po prvku z obou argumentů): hypot, arctan2, copysign, gcd, lcm, maximum, minimum
Funkce pole a skalárního argumentu: round
numpy naučí operace + a * (a další) sčítat resp. násobit pole prvek po prvku, tedy ve smyslu \(c_i = a_i+b_i\) resp. \(c_i = a_i * b_i\). Zatímco u sčítání jde o operaci totožnou se sčítáním vektorů, u násobení ne, skalární součin by dal jedno číslo a o to zrovna zde nestojíme.
viděli jsme ale, že je dovoleno násobit vektor skalární hodnotou (
30*x, tj. \(c_i = k*a_i\)) a podobně bychom mohli ke všem prvkům vektoru přičíst konstantu, kdybychom napsalix+1ve smyslu \(c_i = a_i+q\)
Z toho, co víme o operacích + a * u seznamů, které pro ně také mají svůj (velmi odlišný) význam, nás nepřekvapí, že když plus "vidí" dva operandy typu ndarray udělá jednu akci, když vidí operand typu ndarray a řekněme float, udělá něco jiného. Jde o tzv. přetěžování operátorů, kdy se podle typu operandů zavolá ta či ona funkce. Konkrétní realizaci přetěžování operátorů v jazyce Python si vysvětlíte v navazujících kursech.
Poznámka: Stejný kód jako výše ale s použitím list by vypadal takto:
[ ]:
import matplotlib.pyplot as plt
import math
n = 800
a = 0
b = 10
x = [a+(b-a)*i/(n-1) for i in range(n)]
y = [math.sin(30*t)+1.2*math.sin(31*t) for t in x]
plt.plot(x,y)
plt.show()
Zatím jsme sčítali dvě pole stejné dimenze.
Jako Jeden z důvodů, proč používat numpy, je uváděna rychlost. To proto, že všechny prvky ndarray mají stejný typ a stačí jej tedy zjistit jen jednou. Typicky se tato časová úspora týká i nejkratších vektorů. Nicméně i v případech, kdy to mu tak není přináší numpy pohodlí.
Knihovna je to ovšem rozsáhlá a my v našem kursu musíme vystačit jen s nejmenšími základy. Demonstrujme si, že nám vybraná podmnožina vystačí na následujícím příkladu. V numpy existuje funkce numpy.full, která vrátí pole naplněné danou nenulovou hodnotou. My si ale můžeme nahradit funkcí numpy.zeros a operací + takto:
[ ]:
np.zeros( [2,3] ) + 2
array([[2., 2., 2.],
[2., 2., 2.]])
Monte Carlo
Rozsáhlá část počítačové fyziky používá k určení nějaké hodnoty metody založené na náhodných číslech.
Náhodná čísla, která se používají většinou nepocházejí z fyzikálně náhodného procesu ale taková, jaká vzniknou deterministickým matematickým postupem (garantovaná nepředvídatelnost bývá důležitá spíše u šifrování, řekněme komunikace bankou).
Následující obrázek nám ilustruje, že zatímco siny celých čísel nejsou úplně náhodné, hodnoty, které vrací funkce nump.random.random nemají žádnou zřetelnou pravidelnost.
[ ]:
import numpy as np
import matplotlib.pyplot as plt
# obsazení pole hodnotami
tabulka_int = np.array(range(1000))
tabulka_sin = (np.sin(tabulka_int)-1)/2
tabulka_rnd = np.random.random(len(tabulka_int))
plt.plot(tabulka_int,tabulka_sin,'.')
plt.plot(tabulka_int,tabulka_rnd,'.')
plt.show()
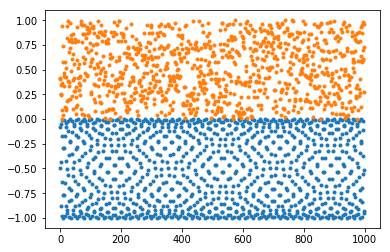
Existuje víc možností, jak může náhodný vstup dát určitý výsledek. My si ukážeme tu, kdy existenci výsledku garantuje zákon velkých čísel.
Klíčový je zde vzorec
v němž se pro velká n počítá průměrná hodnota \(f(x_i)\) pro n náhodně generovaných bodů z intervalu \(<0,1>\) pro 'hezkou' funkci \(f\).
Tyto náhodné body nám v programu poskytuje generátor náhodných čísel a my tento vztah budeme brát jako vlastnost kvalitního generátoru. Proč? Protože například, když položíme \(f(x) = x\), požadujeme vlastně, aby střední hodnota \(<x_i>=1/2\). Tedy nestačí aby čísla byla náhodná, ale musejí být tak náhodná, aby se s jejich rostoucím počtem jejich průměr blížil 0.5. Další funkce otestují další kvality generátoru. Bohužel jsou ještě další podmínky, které generátory náhodných čísel musejí splňovat a "výroba" \(x_i\) tak není jednoduchá záležitost.
Jedno náhodné číslo z intervalu \(<0,1>\) získáme zavoláním funkce random.random(). (Hádejte, jakou knihovnu musíte importovat!) Podobně jedno náhodné číslo vrátí zavolání numpy.random.random().
Protože ale u zákona velkých čísel potřebujeme hodně náhodných hodnot, použijeme v následujícím příkladě příkaz
x = np.random.random(n)
čímž získáme najednou stovku nebo také milióny náhodných čísel podle toho, jaká je hodnota n. Z těch potom najednou spočteme všechna \(f(x_i)\) a pomocí numpy.sum(promenna_typu_pole) i průměr.
[ ]:
# Program demonstruje Monte Carlo kvadraturu
import numpy as np
for k in range(1,8):
n = 10**k
x = np.random.random(n)
# počítáme integrál x^2 sin(1/x^2) pro x od 0 do 1
x2 = x**2
f_x = x2 * np.sin(1/x2)
exact = 0.21884017626889995
approx = np.sum(f_x)/n
err = abs(approx-exact)
print( f"10^{k:1} {approx:21} {err:7.2}" )
10^1 0.42498092364052686 0.21
10^2 0.19729767728815037 0.022
10^3 0.1944514650244184 0.024
10^4 0.22191154362572874 0.0031
10^5 0.2187172448227587 0.00012
10^6 0.21941385985360481 0.00057
10^7 0.2189103309224384 7e-05
Cvičení: Přepište program tak, abyste nepoužívali numpy. Náhodná čísla získávejte prostřednictvím random.random(), trigonometrické funkce jako math.sin.
Zjistěte, kolikrát bude program pomalejší. (Rady: Zmenšete maximální počet náhodných čísel z \(10^7\) na 10000. Odstraňte print. Učiníte-li z programu proceduru, lze snadno použít %timeit.)
 Programování pro fyziky (1.r)
Programování pro fyziky (1.r) Obsah
Obsah