Pole a výpočty lineární algebry
Vektory a matice mají ve fyzice nepřebené množství užití. Proto digitální počítače a jazyky určené k jejich programování braly v úvahu potřeby takových výpočtů, jako je například řešení soustav rovnic.
Zde si na několik příkladech ilustrujeme elementární funkce z lineární algebry, jak se v nich pracuje s poli a jak používat funkce z knihoven.
Jako opakování ověříme, že pro tři konkrétní vektory platí
Napíšeme si fuknci pro skalární součin definovaný vztahem
a také funkci pro vektorový součin.
[4]:
import numpy as np
def scalar_product(a,b):
"Počítá skalární součin dvou vektorů"
dim = len(a)
s = 0.0
for i in range(dim):
s = s + a[i]*b[i]
return s
def vector_product(a,b):
"Počítá vektorový součin dvou vektorů"
assert len(a)==len(b)==3
c = np.zeros(3)
c[0] = a[1] * b[2] - a[2] * b[1]
c[1] = a[2] * b[0] - a[0] * b[2]
c[2] = a[0] * b[1] - a[1] * b[0]
return c
a = np.array([ 1,2,0 ])
b = np.array([ 2,0,1 ])
c = np.array([ 0,1,2 ])
print( vector_product(a, vector_product(b,c)) )
print( b*scalar_product(a,c) - c*scalar_product(a,b) )
[ 4. -2. -2.]
[ 4. -2. -2.]
Problém: Povšimněte si, že obě funkce vracejí správnou hodnotu i tehdy, jsou-li jejich argumenty seznamy typu list nikoli pole numpy.ndarray. Přesto si rozmystlete, na které operaci by program ohlásil chybu, kdybychom proměnné a,b,c inicializovali jako typ list, tedy a = [ 1,2,3 ] atd. Vyzkoušejte, zda Váš odhad vyšel.
Co by se změnilo, kdybychom na čtvrém řádku měli s = 0, tedy celé číslo místo čísla reálného?
Samozřejmě, že v knihovně numpy existují funkce, které počítají totéž. Jmenují se numpy.dot a numpy.cross. Zejména ta první je velmi užitečná a tak ji zanedlouho o něco podrobněji zmíníme znovu.
Cvičení: Napište funkci, která na seznamu vektorů provede Gramm-Schmidtovu ortogonalizaci. (Tento postup akceptuje první vektor v seznamu a od každého dalšího odečítá vhodné násobky těch předchozích, již ortogonálních tak, aby byl každý vektor ortogonální k těm předchozím.)
Rozmyslete si, jak v programu uložíte počáteční a výsledný seznam vektorů.
Rozmyslete si, zda chcete mít funkci, která vrací seznam nebo proceduru, která modifikuje odkazem předávaný argument.
2D a 3D vektory
I u těchto krátkých vektorů sice numpy nepřináší zrychlení výpočtů, ale z hlediska psaní kódu je práce s nimi je pohodlější, protože se hodí, že vektory můžeme sčítat a násobit. Jako příklad si uvedeme klasickou demonstraci vývoje vertikální složky rychlosti ozářením volně padajícího objektu stroboskopem:
[21]:
# Program vykreslí polohy hmotného bodu
# podléhajícímu volnému pádu
# a to v ekvidistantních časových okamžicích
import numpy as np
import matplotlib.pyplot as plt
x0 = np.array([0, 0])
v0 = np.array([1, 9.81])
g = np.array([0,-9.81])
seznam_casu = np.linspace(0, 2, 30)
xy = [ x0 + v0 * t + 0.5 * g * t**2 for t in seznam_casu ]
xy = np.array(xy)
plt.rcParams['axes.facecolor'] = 'black'
plt.axis('equal')
plt.plot( xy[:,0], xy[:,1],'o', color='yellow')
plt.show()
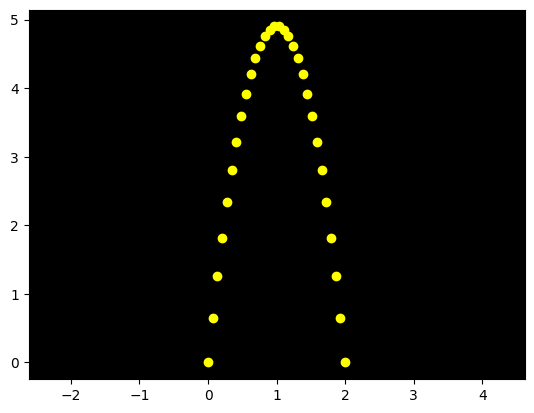
Diskuse:
používáme 2D vektory
chceme vyrobit seznam takových vektorů představující soubor poloh volně padajícího bodu
bohužel pak nemůžeme napsat
v0*seznam_casu, protože definovány jsou jen násobení stejně dlouhých vektorů nebo vektoru a skaláruproto je zkonstruujeme jako
xy = [f(t) for t in seznam_casu]funkce
plotvyžaduje zvlášť x-ové a zvlášť y-ové složky polí, proto používáme řezy, např.xy[:,0]
Cvičení: V kódu se používá seznamový výraz (list comprehension)
xy = [ x0 + v0 * t + 0.5 * g * t**2 for t in seznam_casu ]
xy = np.array(xy)
Přepište tuto pohodlnou konstrukci do podoby cyklu, abyste si vyzkoušeli, jaké to je programovat v běžných jazycích, které tuto vychytávku nemají.
vytvořte pole
xynaplněné hodnotami \(\vec x_0\) (použijtenp.full((len(seznam_casu),2), x0)), tedy polexybude obsahovat tolik 2D vektorů, kolik je počet prvků proměnnéseznam_casupro všechny časy
tz proměnnéseznam_casuk příslušnému prvku pole
xypřičtěte \(\vec v_0 t+ \tfrac12 \vec g t^2\)
V uvedeném návodu je drobná zrada: - pokud budete přičítat příkazem xy[i] = xy[i] + v0 * t + .... program poběží, ale obrázek nebude dobře
pokud budete přičítat příkazem
xy[i] += v0 * t + ....
program ohlásí chybu
Cannot cast ufunc 'add' output ...
Rozmyslete si, v čem chyba spočívá a opravte ji.
Matice a vektory
Jak víme, klíčovou operací je násobení matice vektorem. Knihovna numpy to umí skrze funkci numpy.dot, ale my se to musíme naučit sami:
[33]:
import numpy as np
def matrix_dot_vector(a, x):
dim_x = len(x)
dim_y = len(a)
assert dim_x == len(a[0])
y = np.zeros(dim_y)
for i in range(dim_y):
s = 0.0
for j in range(dim_x):
s = s + a[i,j]*x[j]
y[i] = s
return y
matice = np.array( [
[1,2,3,4],
[1,0,0,1]
])
matrix_dot_vector(matice,[-1,3,-3,1])
[33]:
array([0., 0.])
JIž víme, že knihovna numpy naučí operátory +, * atp. pracovat s poli. Základní podoby jsou
pole * 4, kdy se každý prvek pole vynásobí čtyřmi.pole * pole2, kdy obě pole jsou stejně dlouhá a násobení probího prvek po prvku.
Proto výraz matice*matice2 předpokládá, že obě matice mají stejný tvar a vynásobí je prvek po prvku, tedy podle vzorečku \(c_{ij}=a_{ij} b_{ij}\).
Při práci s poli s více indexy, kde matice jsou nejjednodušším příkladem, je nutné přinejměnším vědět, že je pokud * vložíte mezi matici a vektor, nemusí program nahlásit chybu! Knihovna numpy to pochopí tak, že operaci * použije na každý řádek. Pozor, nejde o násobení \({\mathbb A}\cdot \vec x\) z lineární algebry a tedy dostanete stejný výsledek pro obě pořadí: matice*pole i pole*matice.
[38]:
print( 'matice = \n' , matice , "\n" )
print( 'matice*2 =\n', matice * 2 , "\n" )
print( 'matice * [1,2,3,4] =\n', matice * [1,2,3,4], "\n" )
print( '[1,2,3,4] * matice =\n', [1,2,3,4] * matice , "\n" )
print( 'matice * matice =\n', matice * matice , "\n" )
matice =
[[1 2 3 4]
[1 0 0 1]]
matice*2 =
[[2 4 6 8]
[2 0 0 2]]
matice * [1,2,3,4] =
[[ 1 4 9 16]
[ 1 0 0 4]]
[1,2,3,4] * matice =
[[ 1 4 9 16]
[ 1 0 0 4]]
matice * matice =
[[ 1 4 9 16]
[ 1 0 0 1]]
Knihovna numpy obsahuje velké množství funkcí, které realizují operace z lineární algebry. Z hledniska našeho předmětu - Nehrozí, že bychom vás u zkoušky trápili dotazem: Jak se jmenuje funkce knihovny numpy, která vypočte skalární součin dvou vektorů - Potřebujeme v přednášce praktickou ukázku toho, co to je metoda objektu. Následující řádky se tedy hodí, kdybychom se vás zeptali: Uveďte nějaký příklad proměnné o vhodném typu, kde lze dát příklad volání její metody, a význam takové operace.
Zejména je důležitá funkce numpy.dot. Realizuje operace jako jsou - skalární součin vektorů \(s = x_i y_i\) - součin matice a vektoru \(y_i = \sum_j a_{ij} x_j\) - součin matice a matice \(c_{ik} = \sum_j a_{ij} b_{jk}\)
Máme tři možnosti
funkce
dotz knihovnynumpy, která má dva argumentys = np.dot(vec_x, vec_y)vec_y = np.dot(mat_A, vec_x)mat_C = np.dot(mat_A, mat_B)
použít metodu
dotprvního operandu, která jako argument dostane druhý operands = vec_x.dot(vec_y)vec_y = mat_A.dot(vec_x)mat_C = mat_A.dot(mat_B)
použít operátor
@(ve významu dot)s = vec_x @ vec_yvec_y = mat_A @ vec_xmat_C = mat_A @ mat_B
Cvičení: Napište kód testující devět výše uvedených operací.
Gaussova-Jordanova eliminace
Řešení soustavy lineárních rovnic
si ukážeme za použití Gaussovy-Jordanovy eliminace. Ta pomocí sady ekvivalentních úprav redukuje soustavu rovnic do tvaru, kdy výsledná matice soustavy \(\mathbf A\) je jednotková matice a tedy výsledná pravá strana je hledaným řešením. Jak je obvyklé, spojíme \({\mathbf A}\) a \(\vec b\) do jedné obdélníkové matice \({\mathbf A'}\).
Ekvivalentní úpravy jsou tři: - přehazování rovnic, tedy řádků \({\mathbf A'}\), - násobení rovnic nenulovoým činitelem, - odečítání násobku jedné rovnice od druhé.
Tato metoda je sice pomalejší, než Gaussova metoda se zpětnou substitucí, ale pro naše potřeby dostatečně dobře ilustruje operace, které s maticemi při řešení soustav rovnic provádíme.
Nejprve si ukažme tyto kroky postupně s použitím řezů matic a výhod interaktivního režimu.
[ ]:
import numpy as np
# Nastavíme srozumitelný formát výpisu čísel
np.set_printoptions(floatmode="fixed",precision=4)
# Společná matice soustavy a vektoru pravé strany
matice = np.array( [
[3, 2, 1, 1, 3],
[0, 2, 3, -1, -4],
[1, 9, 0, 4, -5],
[2, 3, 1, 1.0, 0] ] )
# Výpis
matice
array([[ 3.0000, 2.0000, 1.0000, 1.0000, 3.0000],
[ 0.0000, 2.0000, 3.0000, -1.0000, -4.0000],
[ 1.0000, 9.0000, 0.0000, 4.0000, -5.0000],
[ 2.0000, 3.0000, 1.0000, 1.0000, 0.0000]])
Abychom získali na diagonále jedničku, je třeba první řádek vydělit třemi. První řádek matice můžeme zapsat jako matice[0] nebo matice[0,:].
[ ]:
matice[0]
array([3.0000, 2.0000, 1.0000, 1.0000, 3.0000])
[ ]:
matice[0] /= 3
matice
array([[ 1.0000, 0.6667, 0.3333, 0.3333, 1.0000],
[ 0.0000, 2.0000, 3.0000, -1.0000, -4.0000],
[ 1.0000, 9.0000, 0.0000, 4.0000, -5.0000],
[ 2.0000, 3.0000, 1.0000, 1.0000, 0.0000]])
[ ]:
matice[2] -= matice[0]
matice[3] -= 2*matice[0]
matice
array([[ 1.0000, 0.6667, 0.3333, 0.3333, 1.0000],
[ 0.0000, 2.0000, 3.0000, -1.0000, -4.0000],
[ 0.0000, 8.3333, -0.3333, 3.6667, -6.0000],
[ 0.0000, 1.6667, 0.3333, 0.3333, -2.0000]])
[ ]:
# Druhý řádek
matice[1] /= matice[1,1]
matice
array([[ 1.0000, 0.6667, 0.3333, 0.3333, 1.0000],
[ 0.0000, 1.0000, 1.5000, -0.5000, -2.0000],
[ 0.0000, 8.3333, -0.3333, 3.6667, -6.0000],
[ 0.0000, 1.6667, 0.3333, 0.3333, -2.0000]])
[ ]:
matice[0] -= matice[0,1] * matice[1]
matice[2] -= matice[2,1] * matice[1]
matice[3] -= matice[3,1] * matice[1]
matice
array([[ 1.0000, 0.0000, -0.6667, 0.6667, 2.3333],
[ 0.0000, 1.0000, 1.5000, -0.5000, -2.0000],
[ 0.0000, 0.0000, -12.8333, 7.8333, 10.6667],
[ 0.0000, 0.0000, -2.1667, 1.1667, 1.3333]])
[ ]:
# Třetí řádek
matice[2] /= matice[2,2]
matice[0] -= matice[0,2] * matice[2]
matice[1] -= matice[1,2] * matice[2]
matice[3] -= matice[3,2] * matice[2]
matice
array([[ 1.0000, 0.0000, 0.0000, 0.2597, 1.7792],
[ 0.0000, 1.0000, 0.0000, 0.4156, -0.7532],
[-0.0000, -0.0000, 1.0000, -0.6104, -0.8312],
[ 0.0000, 0.0000, 0.0000, -0.1558, -0.4675]])
[ ]:
# Čtvrtý řádek
matice[3] /= matice[3,3]
matice[0] -= matice[0,3] * matice[3]
matice[1] -= matice[1,3] * matice[3]
matice[2] -= matice[2,3] * matice[3]
# Obnovíme výchozí formátování
np.set_printoptions(floatmode="maxprec_equal",precision=8) # set default
# Jsme hotovi
matice
array([[ 1., 0., 0., 0., 1.],
[ 0., 1., 0., 0., -2.],
[-0., -0., 1., 0., 1.],
[-0., -0., -0., 1., 3.]])
Následující funkce GJelim(matice, prava_strana) provádí tyto kroky najednou. Obsahuje navíc kód, který prohazuje řádky. Lze snadno vidět, že by předchozí postup havaroval, kdyby se na diagonále objevila nula, protože tu násobením na jedničku nepředěláme. Protože jsou rovnice záměnné, můžeme přehodit řádky. Pro regulární matici nějaký musí dát nenulový diagonální prvek. Také nás nepřekvapí, že by mohlo vadit i číslo velmi blízké nule. Podrobná analýza ale ukazuje, že je dobré řádky prohazovat
vždy, když lze pod diagonálou najít nějaký větší prvek. Protže by bylo možné ještě navíc prohazovat i sloupce, řáká se takovému postupu částečná pivotace.
Funkce je doplněna o výpis hodnot během výpočtu (print_A(...)), který demonstruje, jak eliminace postupuje.
Na začátku kódu funkce nejprve spojíme matici soustavy a pravou stranu do jediné obdélníkové matice. Nejde o plýtvání časem, stejně bychom si museli pořídit kopie matice i pravé strany, abychom v průběhu eliminace neměnili proměnné, které byly použity při volání.
[ ]:
import numpy as np
def print_A(A, sleep=0.5):
"Výpis upravované matice a pravé strany"
# pro přehlednost skrývám import nepodstatných knihoven
from IPython.display import clear_output
import time
with np.printoptions(floatmode="fixed",precision=3):
print(A)
time.sleep(sleep)
clear_output(wait=True)
def GJelim(matice, prava_strana):
"Vrátí řešení soustavy rovnic A.x=b nalezené GJ eliminací. Parametry musí být typu ndarray."
dim = len(prava_strana)
A = np.zeros([dim,dim+1])
# následující přiřazení provádí zároveň kontrolu velikosti vstupních polí
A[0:dim, 0:dim] = matice
A[0:dim, dim] = prava_strana
for r in range(dim): # pro vsechny radky <r>
print_A(A,sleep=2)
# 1. částečná pivotace (řeší nulovost diagonálního prvku a zvyšuje přesnost)
best_r = r
for r1 in range(r+1,dim):
if abs(A[r1,r]) > abs(A[best_r,r]):
best_r = r1
if best_r != r:
# A[[best_r,r],r:] = A[[r,best_r],r:] #alternativní varianta prohození
print_A(A)
A[best_r,r:], A[r,r:] = A[r,r:], A[best_r,r:].copy()
print_A(A)
# 2. normalizace radku
# 2.1 najdeme prevracenou hodnotu prvku na diagonale
faktor = 1 / A[r,r]
# 2.2 "vsechny" sloupce radku <r> vynasobime timto faktorem
A[r,r:] *= faktor
print_A(A)
# 3. eliminace
for r1 in range(dim): # pro vsechny radky <r1>
if r != r1:
faktor = A[r1,r];
A[r1,r:] -= faktor * A[r,r:]
print_A(A)
print_A(A,sleep=2)
return A[:,dim].copy()
matice = np.array( [
[0, 2, 3, -1],
[3, 2, 1, 1],
[1, 9, 0, 4],
[2, 3, 1, 1] ] )
vektor_ps = np.array( [ -4, 3, -5, 0 ] )
x = GJelim(matice, vektor_ps )
print( ' řešení =', x )
with np.printoptions(precision=1):
print( ' chyba x =', x - [1,-2,1,3] )
print( 'chyba Ax-b =', matice.dot(x) - vektor_ps )
řešení = [ 1. -2. 1. 3.]
chyba x = [-5.6e-16 -8.9e-16 8.9e-16 1.8e-15]
chyba Ax-b = [-8.9e-16 -8.9e-16 -8.9e-16 -8.9e-16]
Dva technické detaily se nám dostaly i do tak jednoduchého programu, jako je řešení soustavy rovnic. Oba souvisí s tím že řezy podle numpy nejsou kopie prvků pole a jen jakési chytré odkazy na původní prvky pole.
Právě proto se v příkazu return A[:,dim].copy() vytváří kopie. Jde o to, že A[:,dim] je poslední sloupec obdélníkové matice A. Ta se zdá být lokální proměnnou funkce GJelim a tedy bychom očekávali, že po skončení běhu funkce paměť zabraná A je uvolněna. Pokud bychom ale funkci ukončili příkazem return A[:,dim] pak by matice A nemohla být zapomenuta, protože její poslední sloupeček představuje řešení soustavy rovnic. Teprve až to by nebylo potřeba, mohlo by se uklidit
i místo pro matici A.
Při prohazování řádek se opět objevuje použití metody copy(). Přitom u prohazování např. celých čísel jsme mohli psát i,j = j,i a nedošlo k potížím. Řezy numpy jsou ale odkazy na pole a jak je vidět níže, zápis matice[2], matice[3] = matice[3], matice[2] způsobí, že řádek obsahující dvojky je přepsán dříve než se jeho hodnota může použít pro prohození. Proto se musí vytvořit "záloha" prostřednictvím copy().
Cvičení: Odstraňte z kódu prohazování řádků a vyzkoušejte, že pro matici
matice = np.array( [
[1e-15, 2, 3, -1],
[3, 2, 1, 1],
[1, 9, 0, 4],
[2, 3, 1, 1] ] )
Bude nalezené řešení soustavy rovnic naprosto špatně a že tedy ono prohazová řádků "za lepší" (částečná pivotace) je nezbytné.
Vzhledem k použití celých řezů můžeme eliminaci zapsat jediným příkazem A[r1,r:] -= A[r1,r] * A[r,r:], tedy pomocnou proměnnou faktor lze vynechat. Kdybychom ovšem prováděli tuto operaci cyklem, pak protože se hodnota prvku pole A[r1,r] během takového cyklu změní, je zapamatování původní hodnoty nezbytné.
Samozřejmě, řešení soustavy rovnic je k dispozici jako funkce numpy.linalg.solve.
Časová náročnost algoritmů
Je zřejmé, že některé výpočty mohou trvat dlouho. Uvažme následující obrázek úplného n-úhelníku pro \(n=7\).
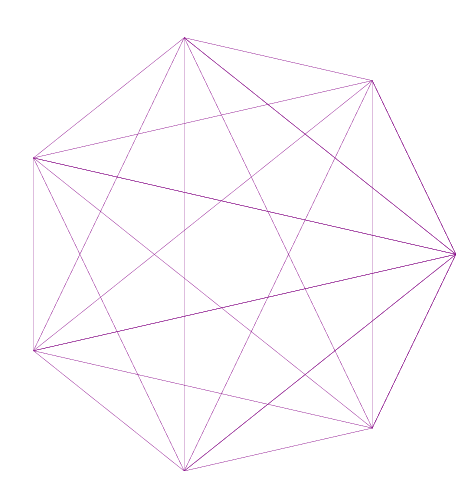
tušíme, že věci se zesložití, pokud vezmeme větší počet vrcholů
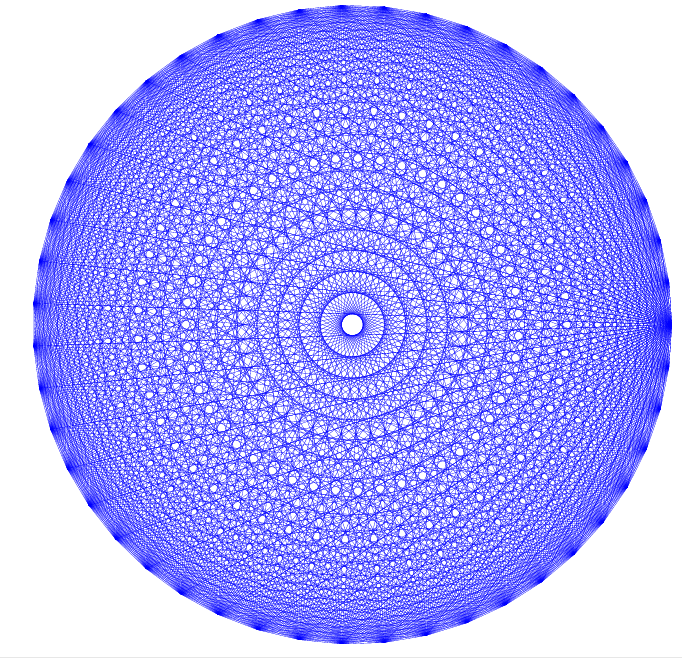
Podobně tomu může být i počítačových programů - při růstu nějakého parametru může doba výpočtu překvapivě prudce. Jak něco takového odhadnout?
Pro každý problém zkusíme najít charakteristické \(N\) číslo udávající jeho velikost. Ne vždy je to možné ale pro představu pár příkladů:
Počet položek na skladu v programu pro skladové hospodářství.
Počet měst, které má navštívit obchodní cestující.
Počet neznámých v soustavě lineárních rovnic.
Počet hvězd tvořících hvězdokupu, jejíž vývoj zkoumáme.
Počet molekul v simulaci.
Nyní se můžeme ptát jak se bude program zabývající se výše uvedenými problémy chovat při růstu onoho charakteristického čísla \(N\). Samozřejmě, pokud neplánujeme růst skladu, zvyšování počtu neznámých atp., nemusíme se tím zabývat. I ve fyzice se ale projevuje tendence počítat složitější a složitější problémy (třeba ty jednodušší už někdo vyřešil) a tak na problém velkého \(N\) můžeme narazit.
Při porovnávání různých algoritmů máme možnost porovnat, jak se chovají pro různé velikosti vstupních dat přímo. Někdy závisí doba řešení problému na konkrétních vstupních hodnotách, často ale, jak jsme viděli, u soustav lineárních rovnic, závisí pouze na velikosti problému.
Vzpomeneme-li si na definici algoritmu, víme že jde o posloupnost elementárních operací. Předpokládejme nejdříve, že elementárními operacemi rozumíme základní operce jako jsou sčítání, násobení, větvení, přístup k jednoduché proměnné, přístup k prvku pole volání či návrat z podprogramu atp. Změříme-li dobu, kterou potřebuje počítač k provedení každé z těchto operací a budeme-li předpokládat, že celý program se vykoná za dobu odpovídající součtu těchto jednotlivých operací, víme jak spočíst dobu potřebnou k provedení programu. Uvažujme podprogram pro skalární součin dvou vektorů o délce \(N\)
def scalar_product(a,b):
"Počítá skalární součin dvou vektorů"
dim = len(a)
s = 0.0
for i in range(dim):
s = s + a[i]*b[i]
return s
Obsahuje různé operacem přičemž např. dim = len(a) se provádní jednou zatímco s = s + a[i]*b[i] se provádí \(N\times\). Mohli bychom tedy nějak zjistit čas provádení jednotlivých operací, ten vynásobit počtem provádění těchto operací, všechny časy sečíst a získat vzorec udávající závislost doby výpočtu na hodnotě \(N\) nap59klad v podobě
Jde o naivní přístup, na moderních počítačích je složité odhadnout dobu výpočtu i kdybychom znali prováděné instrukce procesoru, další komplikace přináší svojí povahou jazyk Python.
Můžeme také zkusit provést experiment:
[60]:
import time
import numpy as np
import matplotlib.pyplot as plt
def scalar_product(a,b):
"Počítá skalární součin dvou vektorů"
dim = len(a)
s = 0.0
for i in range(dim):
s = s + a[i]*b[i]
return s
def time_it(n):
x = np.linspace(0,1,n)
start = time.time()
s = scalar_product(x,x)
end = time.time()
return end - start
n = [2**k for k in range(2, 24)]
t = [time_it(k) for k in n]
plt.plot(n,t)
plt.yscale('log') # logaritmický průběh os
plt.xscale('log')
plt.xlabel('n')
plt.ylabel('čas')
plt.grid()
plt.show()
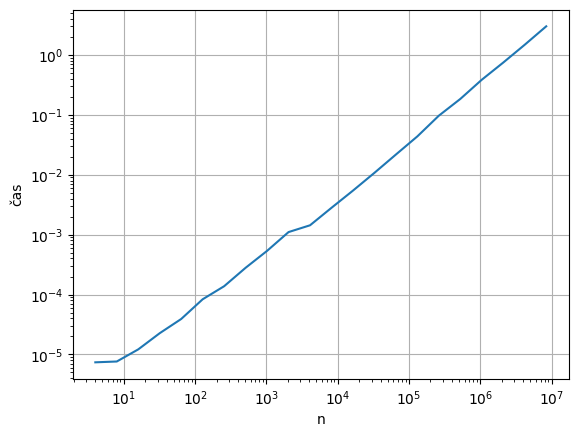
Pohled na obrázek ukazuje, že jde o lineární závislot.
\[T = 36 N^{2} + 44 N +26\]
Pokud nás ale zajímá chování pro větší \(N\), je rozhodující první člen (nejvyšší mocnina). Píšeme tedy
Určit koeficient přesně je ale i tak velmi obtížné, nejsnazší možností je analýza měření závislosti času výpočtu na \(N\) (viz např. graf výše). Pokud chceme mluvit o výkonu algoritmu v okamžiku jeho návrhu ještě před jeho kódováním a nákupem počítače, ukazuje se, že nejjednoduuší je prostě psát
Velké \(O(f)\) je označení pro libovolnou funkci \(g\), která splňuje vztah
Následující tabulka má ilustrovat, že opravdu rozhodující je právě řád, nikoli konkrétní hodnota koeficientu u vedoucího členu.
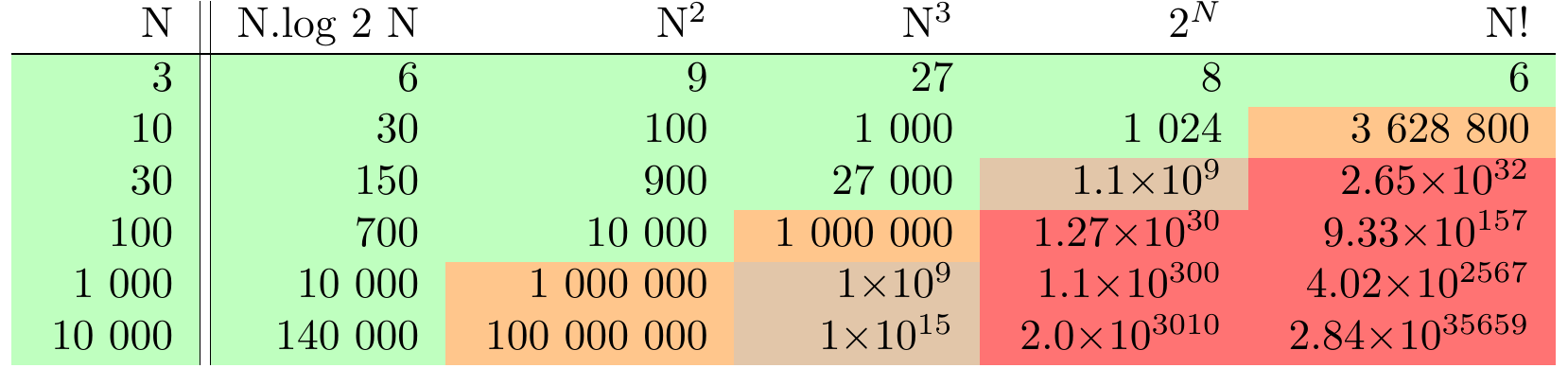
Naše výpočetní možnosti podléhají principiálním omezením, od velkého třesku uplynulo asi \(4\times 10^{26}\) nanosekund a v pozorovaném vesmíru je \(\lessapprox 10^{83}\) atomů.
Vztah \(O(f) . O(g) = O(f . g)\) nám pak umožňuje místo rozkladu algoritmu na elementární kroky O(1), uvažovat strukturovaně.
Třeba Gauss-Jordanova eliminace (za předpokladu, že počet pravých stran je \(\le O(N)\) ) pro každý řádek ( tedy \({\it O(N) }\) krát) provádí
hledání největšího prvku na/pod diagonálou ${:nbsphinx-math:`it O(N) `} $
normalizace \({\it O(N) }\)
odečtení násobku řádku od všech ostatních ${:nbsphinx-math:`it O(N ^{2}) `} $
na začátku a na konci ještě nějaké kopírování \({\it O(N ^{2}) }\)
Odsud máme
V tabulce si pak snadno najdeme, pro jaká \(N\) jde o zelený, oranžový či hnědý problém.
Podobně jako se s rostoucím \(N\) nějak chová čas potřebný k provedení výpočtu, nějak rostou i paměťové nároky. Protože nad velikostí datových struktur máme trochu lepší kontrolu, lze v praxi velmi dobře odhadnout, co se vejde a co ne. V rozvahách o schůdnosti různých algoritmů ale také můžeme použít Landauovu notaci velkého \(O\).
 Programování pro fyziky (1.r)
Programování pro fyziky (1.r) Obsah
Obsah