Další datové typy

Zatím jsme používali

jednoduché datové typy (mj. int, float, bool)
specializované typy (str, textový soubor, objekt reprezentující obrázek atp.)
pole (numpy.ndarray)
seznamy (list, tuple)

Např. pole představovala jasnou ukázku situace, kdy z jednoduššího typu budujeme typ komplikovanější. Také jsme viděli, že typ pole otevřel možnost zapsat širokou oblast nových algoritmů. Existují ale další typy, opět otevírající možnost zapisovat pohodlně další oblasti algoritmů. S některými se v této kapitole seznámíme.

Asociativní pole (`dict`)

V Pythonu jsme zvyklí, že důležité funkce jsou již hotové, takže stačí je jen použít. Podobně je tomu i s datovými strukturami. Jedno z nich jsou tzv. asociativní pole v Pythonu zvané dict. Zatímco u polí a seznamů jsme položku určovali její polohou, tedy indexem, o kterou položku máme zájem se u asociativních polí určuje klíčem. Tedy místo $x[2]$ můžeme psát souradnice["Brno"]. Z hlediska teorie i praxe je důležité, že při růstu počtu položek pole se přístup k prvku (čtení i zápis) chová jako $O(1)$ nikoli jako $O(N)$.

Klíč může být různého druhu, jako příklad použití použijeme klíč v podobě dvojice (tuple) řetězců:

[ ]:

vysledky_zkousek = {}  # založíme prázdný slovník

def zapis_vysledek_zkousky(jmeno, prijmeni, vysledek):
  key = (jmeno,prijmeni)

  if key in vysledky_zkousek:
    vysledky_zkousek[key].append(vysledek)
  else:
    vysledky_zkousek[key] = [vysledek]

def slozil_zkousku(jmeno, prijmeni):
  key = (jmeno,prijmeni)

  if key not in vysledky_zkousek:
    return False

  return min(vysledky_zkousek[key]) < 4

zapis_vysledek_zkousky('Petr', 'Novák', 1)
zapis_vysledek_zkousky('Ivan', 'Dlouhý', 4)
zapis_vysledek_zkousky('Karel', 'Holub', 2)
zapis_vysledek_zkousky('Ivan', 'Dlouhý', 2)

print(f"{slozil_zkousku('Karel', 'Holub') = }")
print(f"{slozil_zkousku('Jan', 'Kolmý') = }")

vysledky_zkousek

slozil_zkousku('Karel', 'Holub') = True
slozil_zkousku('Jan', 'Kolmý') = False

{('Petr', 'Novák'): [1], ('Ivan', 'Dlouhý'): [4, 2], ('Karel', 'Holub'): [2]}

přítomnost klíče v seznamu testujeme operací in
novou hodnotu přidáváme přířazením my_dict[key] = value
stejně modifikuje existující položku slovníku
zmazání položky například del my_dict['key']
operace se slovníky zahrnují mj. spojování {'a':1, 'b':3} | {'b':4, 'c':8} == {'a': 1, 'b': 4, 'c': 8}

Na přednášce si povíme něco o hešování. V Pythonu je možnost použít proměnnou/hodnotu jako klíč dána jejím typem, výše jsme například museli jméno a příjmení spojit do proměnné typu tuple nikoli však list.

Důležité je, že slovník můžeme inicializovat přiřazením, například

barvy = {
 'aquamarine': '#7FFFD4',
 'azure': '#F0FFFF',
 'black': '#000000',
 'blue': '#0000FF',
 'brown': '#A52A2A',
 'cyan': '#00FFFF',
 'darkblue': '#00008B',
 'darkgray': '#A9A9A9'
}

Velmi podobné asociativním polím jsou v Pythonu množiny. U nich není k danému klíči k dispozici jiná informace, než zda do množiny patří či nikoli.

[3]:

n = 5
print(f"Zadejte {n} různých celých čísel.")

numbers = set()
for k in range(n):
  a = int(input("Celé číslo: "))
  if a in numbers:
    print(f"Číslo {a} jste již zadali. Máte špatnou paměť.")
    break

  numbers.add(a)  # zařaď a do množiny numbers

Zadejete 5 různých celých čísel.
Číslo 2 jste již zadali. Máte špatnou paměť.

Složené datové typy

Úvod

Již jsme viděli, že při použití doktríny strukturovaného programování dokážeme s použitím překvapivě málo příkazů (=, if, while, for, ...) a vhodným rozdělením kódu na funkce řešit i komplikované problémy. Stejná doktrína předpokládá, že složitější datové struktury se mohou skládat z jednodušších a programovací jazyk to vhodným způsobem podporuje.

Pokud bychom v přednášce používali jazyk určený pro výuku programování, jako je například Pascal, potkali bychom toto již dávno. V Pythonu jsme aktivně použili zatím jediné strukturování dat: pole (a jim podobné seznamy, tuple, řetězce). Pokud jsme v jedné proměnné chtěli uložit více druhů informace, rozlišovali jsme je hodnotou indexu.

Následující kód demonstruje na příkladě sady barevných kruhů komplikace související s tím, že pokud chceme používat pole z numpy, musíme mít všechny položky stejného typu. Kolečko je přitom zadáno čtyřmi parametry:

x-ovou souřadnicí středu
y-ovou souřadnicí středu
poloměrem
barvou

[ ]:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import CSS4_COLORS  # https://matplotlib.org/stable/gallery/color/named_colors.html

def rgbstr_to_int(s):
    "Převede barvu '#ff00ff' na celé číslo"
    assert s[0] == '#' and len(s) == 7
    return int(s[1:],16)

def disk(x, y, size, color):
    if color[0]!='#':
        color = CSS4_COLORS[color]  # 'red' -> '#ff0000' atp.

    return np.array([x, y, size, rgbstr_to_int(color)])

def pappus_disk(n):
    """viz. https://en.wikipedia.org/wiki/Pappus_chain"""
    r = 0.6

    if n == 'inner':
        return disk(r/2, 0, r/2, 'slategray' )
    if n == 'outer':
        return disk(1/2, 0, 1/2, 'lightgray' )

    w = n*n*(1-r)**2+r
    x = r*(1+r)/(2*w)
    y = n*r*(1-r)/w
    s = (1-r)*r/(2*w)

    return disk(x, y, s, 'lightcoral' if n%2 else 'steelblue' )

def disk_plot(disks, imgsize=6):
    "Namaluje sadu koleček. Parametr imgsize určuje velikost obrázku"

    xmin, xmax = min(disks[:,0]-disks[:,2]), max(disks[:,0]+disks[:,2])
    ymin, ymax = min(disks[:,1]-disks[:,2]), max(disks[:,1]+disks[:,2])
    xcenter, ycenter = (xmax+xmin)/2, (ymax+ymin)/2

    halfwidth = 0.55 * max(ymax - ymin, xmax - xmin)

    factor = imgsize*111    # plt.scatter používá svérázné jednotky velikosti
    sizes = (factor/(2*halfwidth) * disks[:,2])**2 # a velikost udává plochou
    colors= [f'#{int(c):06x}' for c in disks[:,3]] # konverze na #ff8800 atp.

    plt.figure(figsize=(imgsize, imgsize))
    plt.xlim(xcenter - halfwidth, xcenter + halfwidth)
    plt.ylim(ycenter - halfwidth, ycenter + halfwidth)
    #plt.axis(False)

    plt.scatter(disks[:,0], disks[:,1], s=sizes, c=colors )

    plt.show()

# hlavní program
#    - vytvoří sadu koleček
#    - uloží je do proměnné disks
#    - a namaluje je

disks = np.array( [pappus_disk('outer'), pappus_disk('inner')] +
                  [pappus_disk(n) for n in range(-20,21)]      )

disk_plot(disks)

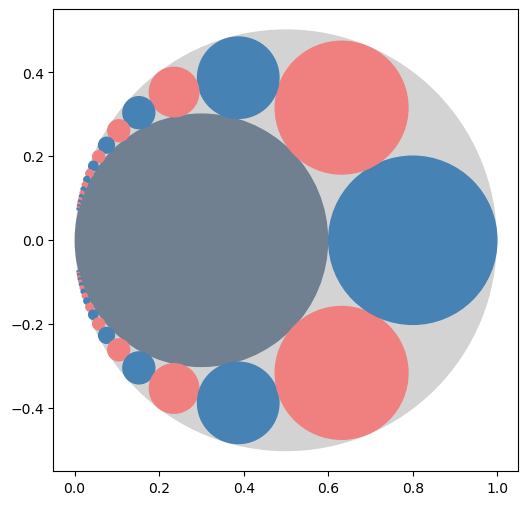
../_images/Prednaska_0110_Posledni_prednaska_5_0.png

Barva ale není přirozeně dána reálným číslem a tak v kódu postupně konvertujeme barvu zadanou jako řetězec do podoby celého čísla a následně reálného čísla. Jako reálné číslo ji uložíme v proměnné disks, ale při vykreslování číslo barvy zase převádíme zpět do podoby řetězce. To vše proto, aby veškerá informace byla uložena v jediné proměnné. To věci natolik komplikuje, že obvykle

použijeme místo polí numpy.ndarray typ list, jehož položky mohou být různého typu, ale ztrácíme komfort řezů ve více indexech , jako je např. disks[:,0] vybírající x-ové souřadnice všech bodů;
pro podobnou sadu koleček použijeme tři proměnné: jedna v podobě pole dimenze $n\times 2$ reálných čísel obsahuje souřadnice středů, další je pole $n$ poloměrů a poslední pak pole $n$ barev;
zavedeme nový typ (viz dále).

Navíc je kód psán nebezpečně, kdybychom přidali ke každému kolečku další atribut, např. hmotnost, mohly by se některé hodnoty indexů změnit a my bychom museli kód procházet a všechny [:,3] měnit na [:,4]. Tomu lze zabránit použitím konstant ve významu hodnot indexů příslušejících jednotlivým položkám. Správně by se takové konstanty měly v Pythonu psát velkými písmeny, takže bychom pak měli

DISK_COORD_X, COORD_Y, DISK_RADIUS, DISK_COLOR = 0, 1, 2, 3
...
    xmin, xmax = min(disks[:,DISK_COORD_X]-disks[:,DISK_RADIUS]), max(disks[:,DISK_COORD_X]+disks[:,DISK_RADIUS])

Takto napsaný kód připraven na zavedení další položky, např. DISK_MASS. Tlak na 'rychlé' psaní kódu ale často vede k opomenutí podobných rad a pak dlouho hledáme, kde nám zbyl neopravený index [3].

Datový typ záznam/struktura

Ve fyzice většinou vystačíme (či budeme nuceni vystačit) s postupem uvedeným výše. Přesto je rozumné vědět, že již dlouho nabízejí programovací jazyky možnost vytvořit nový datový typ sdružují do jedné entity všechny potřebné položky, ať už jsou jakéhokoli typu a při použití takové proměnné lze pak

uvést jen identifikátor proměnné a tím zacházet s uvažovanými daty jako celkem, např. funkce overlap(d1, d2) zjistí, zda se dva disky překrývají.
uvést identifikátor proměnné následovaný tečkou a specifikací atributu, např. podmínka d1.radius > abs(d1.y) testuje, zda diskem d1 prochází osa x.

V Pythonu je tohle bohužel komplikováno principem, že přiřazení znamená odkaz na existující data a tak zavedení nového typu oproti běžným jazykům neznamená popis uložení položek v novém typu, ale rovnou návod jak data takového typu vytvořit.

Minimální kód vytvářející proměnnou popisující disk podle minulého příkladu je:

[ ]:

class ColorDisk:
    x = 0
    y = 0
    radius = 0
    color = '#000000'


def disk(x, y, size, color):
    d = ColorDisk()
    d.x = x
    d.y = y
    d.radius = size
    d.color = color

    return d


d1 = disk(0,0,1,'blue')

Povšimněte si příkazu d = ColorDisk(). Ten ukazuje, že zavedením class ColorDisk jsme také založili stejnojmennou funkci, která

se použije, když potřebujeme vytvořit data daného typu. To že jde o nový typ indikuje výsledek výrazu type(d1).

Vidíme, že v tomto příkladě se zbytečně nejprve nastaví x na hodnotu nula a teprve poté na požadovanou hodnotu. To proto, že jsme nepoužili podstatu objektového programování a spolu s novou třídou jsme nezavedli její konstruktor/inicializátor __init__. Podobně, abychom mohli k výpisu obsahu proměnné používat print(d1), potřebovali bychom zavést metodu __str__. S tím vším se seznámíte v nějakém kurzu jazyka Python, do našich 'základů' se objektové programování již nevejde.

Je zajímavé, že i zběhlí uživatelé jazyka Python toto považovali za natolik komplikované (otravné), že pro zjednodušení zavedli automatizaci těchto kroků za použití knihovny dataclasses. Protože její použití činí zavedení nového typu velmi podobným jazykům jako je C nebo Pascal, použijeme tuto knihovnu a ukážeme si na ní práci s nově zavedeným typem zavádějícím strukturu/záznam.

[ ]:

from dataclasses import dataclass

@dataclass       # proveď výše zmíněnou automatizaci
class ColorDisk:
    x : float
    y : float
    radius : float
    color : str = 'black'

d1 = ColorDisk(0, 0, 1, 'blue')
d2 = ColorDisk(1, 0, 0.5)

print(d2)

ColorDisk(x=1, y=0, radius=0.5, color='black')

Zde vidíme, že nový typ je složený z položek, které

mají své jméno (uvádí se za tečkou, tedy např. d1.x);
mají svůj typ;
se inicializují v rámci volání ColorDisk(...) hodnotami argumentů v pořadí, v jakém jsou definovány příkazem class;
mohou podobně jako v případě argumentů funkcí mít výchozí hodnotu, takže si ve druhém případě ušetříme uvedení barvy kolečka.

Konverze na řetězec, kterou automaticky volá příkaz print pak vrací srozumitelnou informaci o dané proměnné.

Příklad na použití vlastní datové struktury

[ ]:

"""
Program řeší srážení volně se pohybujících kruhových disků.
"""

import math
from dataclasses import dataclass
import matplotlib.pyplot as plt
from matplotlib import animation
from IPython.display import HTML

# každý z disků má 2D polohu a rychlost, hmotnost, poloměr a barvu
@dataclass
class ColorDisk:
    x : float
    y : float
    vx : float
    vy : float
    r : float
    m : float
    color : str = 'blue'


DISK_FIXED = 1e40    # dostatečně těžký disk se při srážce nepohne

def bounce(a, b):
   """
   Modifikuje rychlosti v důsledku plně elastického odrazu
   viz https://en.wikipedia.org/wiki/Elastic_collision#Two-dimensional_collision_with_two_moving_objects
   """

   delta_r2 = (a.x-b.x)**2 + (a.y-b.y)**2

   assert abs( delta_r2 - (a.r+b.r)**2 ) < 1E-10, 'Disky se nedotýkají!'

   deltav_dot_deltar = (a.vx-b.vx)*(a.x-b.x) + (a.vy-b.vy)*(a.y-b.y)
   factor = 2*deltav_dot_deltar/(delta_r2 * (a.m+b.m))

   a.vx = a.vx - b.m*(a.x-b.x)*factor
   a.vy = a.vy - b.m*(a.y-b.y)*factor

   b.vx = b.vx + a.m*(a.x-b.x)*factor
   b.vy = b.vy + a.m*(a.y-b.y)*factor


def time_to_bounce(a, b):
  """
  Výpočet času zbývajícího do srážky dvou disků.
  Pokud se v budoucnu nepotkají, vrací funkce záporné číslo.
  """

  d2 = (a.r+b.r)**2
  x2 = (a.x-b.x)**2 + (a.y-b.y)**2

  if x2-d2 < -1E-7:
    # povolujeme protínající se těžké disky tvořící arénu
    assert a.m == b.m == DISK_FIXED, f'Disky se protínají! ({x2-d2=} {a=} {b=})'
    return -1

  v2 = (a.vx-b.vx)**2 + (a.vy-b.vy)**2
  if v2 == 0:
    return -1   # disky se vůči sobě nepohybují

  deltav_dot_deltar = (a.vx-b.vx)*(a.x-b.x)+(a.vy-b.vy)*(a.y-b.y)
  discriminant = deltav_dot_deltar**2 - v2*(x2-(a.r+b.r)**2)
  if discriminant <= 0:
    return -1   # disky se míjejí

  return (-deltav_dot_deltar-math.sqrt(discriminant))/v2



###############################################
###   Vykreslení disků
###############################################

def plot_frame():
  """Vykresli disky. Pro jednoduchost založeno na funkci pyplot.scatter."""
  plt.gca().clear()   # musíme smazat minulý obrázek

  plt.xlim(-1, 1)
  plt.ylim(-1, 1)
  plt.axis(False)

  factor = 111*imgsize/2    # plt.scatter používá svérázné jednotky velikosti

  displayed_disks = disks[4:]

  x = [d.x for d in displayed_disks]
  y = [d.y for d in displayed_disks]
  colors = [d.color for d in displayed_disks]
  sizes = [(factor * d.r)**2 for d in displayed_disks]

  plt.scatter(x, y, s=sizes, c=colors )


###############################################
###    Evoluce
###############################################

def advance_time(new_time):
  """Posune disky podle jejich rychlosti a upraví čas.
  Předpokládá, že za dobu dt nedojde ke srážce."""
  global time

  dt = new_time - time
  for p in disks:
    p.x = p.x + p.vx*dt
    p.y = p.y + p.vy*dt

  time = new_time

###############################################
###   Animace
###############################################

fps = 16.0
time = 0
next_bounce_time = -1    # signalizuj, že je třeba jej spočíst
m_next, n_next = -1, -1

def draw_frame(i):
  """Vykreslení i-tého snímku animace."""

  # Bohužel plt.scatter nefunguje s ArtistAnimation a tak se musí používat metoda
  # FuncAnimation, která vyžaduje callback pro každý snímek.
  # funkce draw_frame proto vždy posune čas do okamžiku dalšího snímku

  global time, next_bounce_time, m_next, n_next

  frame_time = i * dt_frame
  assert frame_time >= time, "neumím nechat plynout čas nazpátek"

  # 1. vyřeš srážky předcházející vykreslení snímku
  while next_bounce_time < frame_time:
    # 1.1 proveď pohyb disků a následný odraz
    dt = next_bounce_time - time
    if dt>=0:  # ignoruj signalizaci neznalosti času srážky
        advance_time(next_bounce_time)
        bounce(disks[m_next], disks[n_next])

    # 1.2 spočti čas příští srážky
    dt_min = 1e100                   # nikdy se nesrazí
    for m in range(len(disks)):
      for n in range(m):             # stačí testovat n < m
        dt = time_to_bounce(disks[m], disks[n])
        if dt >= 0 and dt < dt_min:   # najdi nejmenší nezáporné dt
            dt_min, m_next, n_next = dt, m, n

    next_bounce_time = time + dt_min

  advance_time(frame_time)  # 2. posuň čas do okamžiku snímku
  plot_frame()              # 3. vykresli polohu disků


def some_color(i,j):
  return f'#{11247*i+13697*j & 0xf8f8f8:06x}'

###############################################
###   Seznam disků
###############################################
b0 = 100
r0 = b0 - 1
disks = [ColorDisk(-b0,0,0,0,r0,DISK_FIXED),
         ColorDisk(+b0,0,0,0,r0,DISK_FIXED),
         ColorDisk(0,-b0,0,0,r0,DISK_FIXED),
         ColorDisk(0,+b0,0,0,r0,DISK_FIXED)]

h = 1/16
for i in range(-6,7,3):
  for j in range(-6,7,3):
    disks.append( ColorDisk(i*h, j*h, 0, 0, h, 1, some_color(i,j)) )

disks[4].vx = 5
disks[4].vy = 2


###############################################
###   Vytvoření animace
###############################################
imgsize = 6      # proměnnou používá i plot_frame()
fig = plt.figure(figsize=(imgsize, imgsize))

time_factor = 0.2   # jak rychle plyne čas v simulaci
dt_frame = (1/fps) * time_factor

ani = animation.FuncAnimation(fig, draw_frame, frames=400, interval=50)

tmp = ani.to_html5_video()
plt.close()
HTML(tmp)

Poznámky:

Vzpomeňte si, proč uvnitř funkce advance_time je global time ale nikoli global disks, když stejně jako čas, funkce mění i polohy disků.
Funkce some_color generuje řetězec nějaké barvy v podobě "#rrggbb". Vhodně zvolená konstanta v logickém součinu zařídí, že formátovaný výstup celého čísla závislého na i a j má šest hexadecimálních cifer a zároveň disk nebude úplně bílý, aby se ztratil na pozadí.
Aby nebyl kód dlouhý používáme knihovnu matplotlib. O vykreslování se stará scatter, animaci přenecháváme funkci FuncAnimation. Bohužel,

Rozbalování polí představujících struktury

Ještě se vraťme k situaci, kdy nás okolnosti nutí používat pro uložení podobných dat pole numpy.ndarray. V takovém případě můžeme použít rozbalení (unpacking) do sady vhodně pojmenovaných proměnných a psát:

def bounce(a, b):
   # založíme a_x, ...
   a_x, a_y, a_vx, a_vy, a_r, a_m, a_color = a
   b_x, b_y, b_vx, b_vy, b_r, b_m, b_color = b
   # používáme je místo a[0], ...
   delta_r2 = (a_x-b_x)**2 + (a_y-b_y)**2
   ...
   b_vy = b_vy + a_m*(a_y-b_y)*factor
   # změněné hodnoty nutno uložit zpět do odkazem předaných polí
   a[2:4] = a_vx, a_vy
   b[2:4] = b_vx, b_vy

tedy ve výpočtech, používat srozumitelný zápis b_vy místo nebezpečného b[2] nebo nepohodlného b[VX].

Podobný trik jsme použili při řešení soustav obyčejných diferenciálních rovnic, kde numerické metody vyžadují, abychom pracovali s polem, ale jeho jednotlivé složky mají jednou význam poloh, jindy rychlostí, takže rozbalení / sbalení mělo podobu

def pohybova_rovnice_planety(t, U):
  "Předpokládá U = [x,y,vx,vy]. Vrací časovou derovaci U dle Newtona."
  x, y, vx, vy  = U
  ...
  return np.array([vx, vy, ax, ay])

Dynamické datové struktury

Již pole a seznamy umožňovaly měnit počet jejich prvků (ale u polí se to nedoporučuje). Pokud v závislosti na stavu výpočtu nabývá seznam různé délky, jde o nejjednodušší příklad dynamické datové struktury. V historii programování se nicméně objevily ještě složitější datové struktury. Důležitou podmnožinu tvoří stromy. Potkáme se s ním často, například výraz

\[\frac{1 + x^2}{1 - x}\]

lze (jak to dělá SW Mathematica) zapsat jako stromový graf

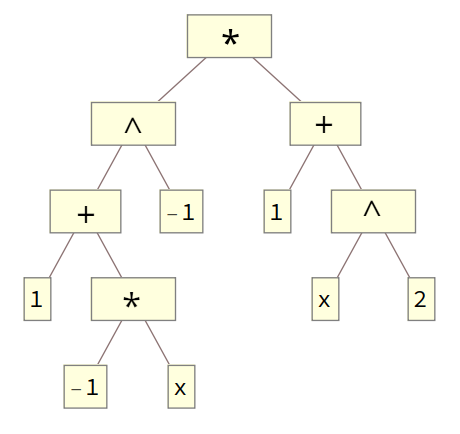
výraz

Program, který umí pracovat s takovýmito výrazy musí dokázat v nějaké proměnné udržet informaci o libovolném výrazu, takže není možné mít fixní datovou strukturu, jako by například bylo racionální číslo (vždy jeden čitatel a jeden jmenovatel). Navíc, při úpravách mohou nové výrazy vznikat a nebo zanikat.

Zatímco v jazycích, jako je C, musíme věnovat hodně pozornosti již navržení vhodného typu a pak i práci s ním, jazyk Python nám ledacos skryje.

Zapomeneme na mocnění a zkusíme vystačit s operacemi +,* a operandy v podobě celých čísel, proměnných a funkcí.

[9]:

# Ukázka reprezentace výrazu jako stromu. Implementuje jen malou podmnožinu výrazů:
#
# vyraz je
#    celé číslo
#    'název_proměnné'
#    ['+', výraz, výraz (, výraz , ...) ]
#    ['*', výraz, výraz (, výraz , ...) ]
#    ['název_fce', výraz (, výraz , ...) ]

def to_str(e):
    "Vrátí řetězec odpovídající výrazu e"

    if type(e) == int:
        return str(e)  # 3

    if type(e) == str:
        return e       # x

    assert type(e) == list

    if e[0] == '+':    #  x + 3*z
        return ' + '.join([to_str(a) for a in e[1:]])

    if e[0] == '*':    #  x*y nebo  x*(y+z)
        return '*'.join(['('+to_str(a)+')' if type(a)==list else to_str(a) for a in e[1:]])

                       #  sin(x)
    return e[0]+'('+','.join([to_str(a) for a in e[1:]])+')'

def diff(e,x):
    "Vrátí parciální derivaci výrazu e podle x"

    if type(e) == int:
        return 0

    if type(e) == str:
        return int(e == x)

    assert type(e) == list

    if e[0] == '+':
        de = [diff(a,x) for a in e[1:]]
        return ['+'] + de

    if e[0] == '*':
        de = [diff(a,x) for a in e[1:]]
        s = ['+']
        for i in range(len(de)):
            s1 = e[1:]   # řezy typu list jsou kopie
            s1[i] = de[i]
            s.append(['*'] + s1)
        return s

    assert False, "Derivace funkcí nejsou implementovány"

def int_product(a):
    p = 1
    for x in a:
        p = p * x

    return p


def normal(e):
    "Provede částečnou normalizaci výrazu, např 1*(x-3)+4 -> x+1, chybí mj. x+x -> 2*x"
    if type(e) != list:
        return e

    f = e[1:]
    for i in range(len(f)):
        f[i] = normal(f[i])

    if e[0] != '+' and e[0] != '*':
        return [e[0]] + f

    if e[0] == '+':
        ff = []
        for a in f:
            if type(a)==list and a[0]=='+':
                for b in a[1:]:    #  x*(y*z) -> x*y*z
                    ff.append(b)
            else:
                ff.append(a)

        f1 = sorted([a for a in ff if type(a)==str])
        f2 = [a for a in ff if type(a)==list]
        f3 = [a for a in ff if type(a)==int]

        assert(len(f1)+len(f2)+len(f3)==len(ff))

        f3=[sum(f3)]
        if f3[0] == 0 and len(f1)+len(f2)>0:
            f3 = []

        f = f1+f2+f3
        if len(f)==1:
            return f[0]
        return ['+'] + f

    assert e[0] == '*'

    ff = []
    for a in f:
        if type(a)==list and a[0]=='*':
            for b in a[1:]:
                ff.append(b)
        else:
            ff.append(a)

    f1 = sorted([a for a in ff if type(a)==str])
    f2 = [a for a in ff if type(a)==list]
    f3 = [a for a in ff if type(a)==int]

    assert(len(f1)+len(f2)+len(f3)==len(ff))

    f3 = [int_product(f3)]
    if f3[0] == 0:
        return 0        # 0*x -> 0

    if f3[0] == 1 and len(f1)+len(f2)>0:
        f3 = []         # 1*x  -> x

    f = f3+f1+f2
    if len(f)==1:
        return f[0]
    return ['*'] + f



expr1 = ['*',
         ['+', 'x', -2],
         ['+', 'x',  2]
        ]
expr2 = diff(expr1,'x')
expr3 = normal(expr2)

print( 'expr1 = ', to_str(expr1) )
print( 'expr2 = ', to_str(expr2) )
print( 'expr3 = ', to_str(expr3) )

expr1 =  (x + -2)*(x + 2)
expr2 =  (1 + 0)*(x + 2) + (x + -2)*(1 + 0)
expr3 =  x + x

Rozmyslete si

jak zařídit, aby výraz jako $x+y+x$ byl normalizován do podoby $2x+y$,
jak by vypadala funkce subs(e,d), která by do výrazu $e$ za proměnné dosadila hodnoty (případně výrazy) podle tabulky $d$, např: subs(expr1,{'x':1, 'y':2}),
co vše by se muselo doplnit, aby bylo možno spočíst derivace výrazů obsahujících funkce.

Nám zápis výrazu umožnil demonstrovat na konkrétním příkladě, co to je dynamická datová struktura. Počítačová manipulace s algebraickými výrazy je ovšem seriozní obor, který se vyvíjí již mnoho desetiletí. V některých oblastech fyziky počítačová algebra nabízí možnost zvládat vzorečky s miliony členů. Mezi knihovnami Pythonu je balík SymPy, studenti MFF UK mají nárok na instalaci ještě mnohem rozsáhlejšího SW Mathematica.

Jak zrychlit výpočet

Pokročilejší matematika a fyzika:

Na příkladě výpočtu numerické hodnoty $\pi$ uvidíme, že zrychlení může být ohromné:
- Pokud bychm počítali podle vztahu
  
  \[\pi = 4 \sum_{k=0}^\infty \frac{(-1)^k}{2 k + 1}\]
  
  tak ten má ma chybu $\approx \pm 1/n$, kde $n$ udává horní mez u které ukončíme sčítání řady. Pro deset cifer bychom tak potřebovali deset miliard sčítanců.
- Ukazovali jsme si tzv. Richardsonovu etrapolaci. Ta zde funguje a polynomiální extrapolací hodnot sumy pro $30, 60, 90, 120, 150$ sčítanců získáme správně 10 cifer $\pi$. (Viz též naše ukázka Rombergovy kvadratury)
- Ramanujan navrhl řadu
  
  \[\frac{1}{\pi} = \frac{2 \sqrt 2}{99^2} \sum_{k=0}^\infty \frac{(4k)!}{k!^4} \frac{26390k+1103}{396^{4k}}\]
  
  u níž stačí vzít první dva sčítance a máme 13 cifer $\pi$ správně.
Na úrovni programování je obdobou lepšího vzorečku lepší algoritmus. (Viz quicksort níže.)
Výjimečně pomůže lepší překladač (tohle se týká Pythonu, viz numba)
Poslední, ovšem velmi pracné řešení představuje paralelismus. Mirný (váš domácí počítač má možná i deset jader) nebo masivni (graf. karty a clustery počítačů).

Urychlení běhu programů Pythonu s použitím knihovny `numba`

Připomeňme si, že Python obětoval rychlost vykonávání kódu vyšším cílům. Proto zatímco procedura v jazyce C

int x;

void zvetsi_x(int n)
{
   x = x + n;
}

přeloží proceduru do strojového kódu o dvou instrukcích procesoru - jedné zařizující sčítání add variable_x, register_edi a jedné pro návrat z procedury ret, musí být Python připraven u kódu

def zvetsi_x(n):
    global x
    x = x + n

zvětšit libovolný typ globální proměnné x podoporující sčítání:

[5]:

import numpy as np

def zvetsi_x(n):
    global x
    x = x + n

x = 40
zvetsi_x(2)
print(x)

x = np.zeros(10)
zvetsi_x(2)
print(x)

42
[2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]

Výchozí interpret jazyka Python tzv. CPython tuto přitěžující (zpomalující) okolnost bere jako danost s tím, že pro výkon programu klíčové funkce se nepíší v Pythonu, ale používají se jejich varianty z nějaké vhodné dobře optimalizované knihovny.

Existují ale nástroje, které se snaží vykonávání příkazů Pythonu přiblížit procesoru. My v této přednášce pro jednoduchost použití volíme funkci njit z knihovny numba. Ta pro daný typ argumentů vyrobí přeloženou variantu funkce. K času běhu prvního volání funkce se tak přičítá čas potřebný pro překlad, při dalších voláních se ale její rychlost za příznivých okolností může přiblížit ekvivalentnímu kódu v C. Použití njit má však mnoho omezení. U výše uvedeného příkladu například odmítne modifikovat globální proměnnou. Pokud překlad pomocí njit selže, dozvíme se o tom a máme šanci kód upravit.

To, že zrychlení pomocí njit je podstatné, demonstruje i následující kód pro výpočet polohy těžiště metodou Monte Carlo. I když generování náhodných čísel voláním funkce random.random() zabere hodně času, stále njit přinese 14x rychlejší výpočet.

Monte Carlo II (ukázka použití `numba.njit`)

Již jsme viděli, že náhodná čísla vytvářená v počítači ve velkém počtu umožní spočíst nenáhodný výsledek (například určitý integrál). Ještě jednou se k tomu vrátíme na příkladu výpočtu těžiště objektu. Objasníme si znovuy princip metody a navíc porovnáme dva styly, jak psát příslušný kód.

Budeme počítat polohu těžiště polokoule z homogenního materiálu. V principu jde o výpočet

\[\vec x_T = \frac{\int_V \vec x\; dm}{\int_V dm}, ~~~ dm = \rho\; dV.\]

Povšimněme si, že pokud by místo materiálu s pravidelným uspořádáním atomů šlo o ideazovaný plyn tvořený stejně hmotnými atomy, poloha těžiště by se nezměnila, ale těžiště by bylo dáno sumou místo integrálu

\[\vec x_T = \frac{\sum m_i\; \vec x_i }{\sum m_i} = \frac{1}{N}\sum \vec x_i .\]

Těžiště tělesa lze tedy určit jako průměr poloh atomů "plynu" těleso homogenně vyplňujícího.

Rovnoměrné rozložení plynu budeme modelovat použitím (pseudo-)náhodných poloh. Klíčové je důležité pozorování: Homogenní rozložení dosáhneme obráběním jiného homogenního rozložení, nikoli však "kováním", kdy v místech kde nám tvar nevyhovujeme přebývající materiál vměstnáme do nějaké formy. U náhodných čísel to bude znamenat zahazovat body (představující atomy) ležící mimo polokouli.

[10]:

from random import random
from numba import njit

@njit
def nahodny_bod_polokoule():
    while True:
        x = 2*random() - 1
        y = 2*random() - 1
        z = random()

        if x*x + y*y + z*z < 1:
            return x, y, z

@njit
def teziste_polokoule(n):

    xT,yT,zT = 0.0, 0.0, 0.0
    for i in range(n):
        x,y,z = nahodny_bod_polokoule()
        xT += x
        yT += y
        zT += z

    return  xT/n, yT/n, zT/n


teziste_polokoule(10**2)   # zavoláme funkci, aby proběhl její překlad a ten nezapočítával do měření času %time
%time teziste_polokoule(10**6)

CPU times: user 72.1 ms, sys: 0 ns, total: 72.1 ms
Wall time: 72.1 ms

[10]:

(-0.0006740258738324543, 8.31535722820731e-06, 0.3751882573340752)

Můžete experimentováním zkoumat jak dobře se pro rostoucí počet bodů spočtená poloha těžiště blíží hodnotě $3/8$.

QuickSort (ukázka chytrého/rychlého algoritmu třídění)

Vnitřní třídění seznamu znamená seřazení seznamu, které se odehrává uvnitř počítající části počítače a ne třeba na magnetické pásce, proto vnitřní. Historicky totiž první počítače neměly dost paměti, aby se tam tříděná data vešla najednou, takže existovala i disciplína vnějšího třídění.

Pro třídění potřebujeme mít definovanou funkci $\le$ dvou parametrů typu položky pole k setřídění. Část položky, která obsahuje informaci potřebnou pro porovnání se nazývá klíč. Obvykle z klíče nevyplývá přímo poloha v setříděném seznamu a má význam jen při porovnání s jiným klíčem.

Seznam považujeme za setříděný, platí-li

\[A_1 \le A_2 \le A_3 \le ... \le= A_N\]

Viděli jsme, že bubble sort obsahuje dva cykly a je jasným příkladem $O(N^2)$ algoritmu. V začátcích informatiky se hrály třídící algoritmy důležitou roli a jejich rozbor je v tomto oboru stále důležitý. Ačkoli jako fyzikové budeme používat funkce poskytující implementaci nějakého efektivního algoritmu, je zážitek porovnání neefektivního (např. bubblesort) a efektivního (např. quicksort) algoritmu důležitý pro každého, kdo programuje. Nejprve si tedy zopakujme tedy třídění probubláváním.

[11]:

import numpy as np
from numba import njit

@njit
def buble_sort_inplace(a):
    """procedura setřídí pole, které dostane jako parametr. Nic nevrací. Učíme se na ní práci s poli, jinak je buble sort na nic."""

    n = len(a)

    for i in range(n-1,0,-1):
        for j in range(i):
            if a[j]>a[j+1]:
               a[j], a[j+1] = a[j+1], a[j]



arr = np.random.randint(0,100, 20)
buble_sort_inplace(arr)
print("Krátký test setřídění:")
print(arr)

arr = np.random.randint(0,100, 10**5)

%time buble_sort_inplace(arr)

Krátký test setřídění:
[ 4 12 16 20 22 25 29 32 39 47 48 50 63 75 76 77 77 81 94 98]
CPU times: user 12 s, sys: 8.02 ms, total: 12 s
Wall time: 12 s

Quicksort je název algoritmu (Hoare cca 1960), který většinou dokáže seřadit seznam v čase $O(N \log N)$. Využívá toho, že do přesné polohy položky mají nejvíce co mluvit ty sousední. Proto:

Zvolí některou hodnotu ze seznamu jako tzv. pivot.
Rozdělí celý seznam bez pivotu na dvě skupiny: tu, kde jsou položky menší než pivot a zbytek.
Poté za použití rekurze předá obě části sám sobě k seřazení. Pokud nám minulý krok rozdělí pole na zhruba dvě stejně velké části, dostáváme, podobně jako metody u půlení intervalu, jen logaritmický počet kroků, kterých je zapotřebí, abychom došli k seznamu délky 1, který již není třeba třídit.

Potíž spočívá v tom, že položku, podle které rozdělujeme seznam na dvě části, vezmeme aniž víme jestli je blízko "prostředku". Proto se může stát, že pro nevhodně uspořádaný vstup vezmeme vždy tu nejmenší/největší a skočíme u časové náročnosti O(N$ ^{2)} $.

Rozdíl mezi $O(N^2)$ a $O(N \log N)$ je ukázán zde.

Pedagogická varianta kódu, jakou v mnoha podobách najdeme v učebnicích Pythonu vytváří seznam menších a větších prvků, ty nechá rekurzivním voláním seřatit a vrátí spojený seznam. Za pivot bere první prvek. To je názorné, ale ne moc rychlé. Navíc intezivní užití seznamů brání použití akcelerace @njit.

[7]:

import numpy as np

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        left = [x for x in arr[1:] if x < pivot]
        right = [x for x in arr[1:] if x >= pivot]
        return quicksort(left) + [pivot] + quicksort(right)

# Example usage
arr = list( np.random.randint(0,100, 20) )
sorted_arr = quicksort(arr)
print("Krátký test třídění:")
print(sorted_arr)
print("Dlouhý test třídění:")
arr = np.random.randint(0,100, 10**5)
%time sorted_arr = quicksort(arr)

Krátký test třídění:
[0, 3, 3, 9, 19, 39, 58, 62, 62, 66, 66, 69, 70, 71, 71, 78, 85, 86, 97, 97]
Dlouhý test třídění:
CPU times: user 5.68 s, sys: 0 ns, total: 5.68 s
Wall time: 5.68 s

Rychlejší rozdělení probíhá přehazováním položek, které do příslušných částí nepatří a předáváním odkazu na pole a informace jako jeho část je potřeba seřazovat. Zde již provádíme samé "jednoduché" operace a lze použít akceleraci @njit.

[13]:

import numpy as np
from numba import njit

@njit
def quicksort(arr, l=0, r=-1):
    if r<0:
        r = len(arr)-1

    pivot = arr[(l + r) // 2]

    i, j = l, r
    while i<j:
        while arr[i] < pivot:
            i = i + 1
        while pivot < arr[j]:
            j = j - 1
        if i <= j:
           arr[i], arr[j] = arr[j], arr[i]
           i = i + 1
           j = j - 1
    if l < j:
        quicksort(arr, l, j)
    if i < r:
        quicksort(arr, i, r)


# Použití
arr = np.random.randint(0,100, 20)
quicksort(arr)
print("Krátký test třídění:")
print(arr)
print("Dlouhý test třídění:")
arr = np.random.randint(0,100, 10**5)
%time quicksort(arr)

Krátký test třídění:
[ 7 21 26 29 29 32 36 43 50 52 55 73 75 75 78 83 93 98 98 99]
Dlouhý test třídění:
CPU times: user 5.91 ms, sys: 0 ns, total: 5.91 ms
Wall time: 5.91 ms

To, že kód je 700x rychlejší má dva důvody. Faktorem 90 přispěje numba, zbytek dá vynechání konstrukce nových seznamů uvnitř každého kroku tím, že spoléháme na in place přehazovaní prvků ležících v nesprávné "polovině" pole.

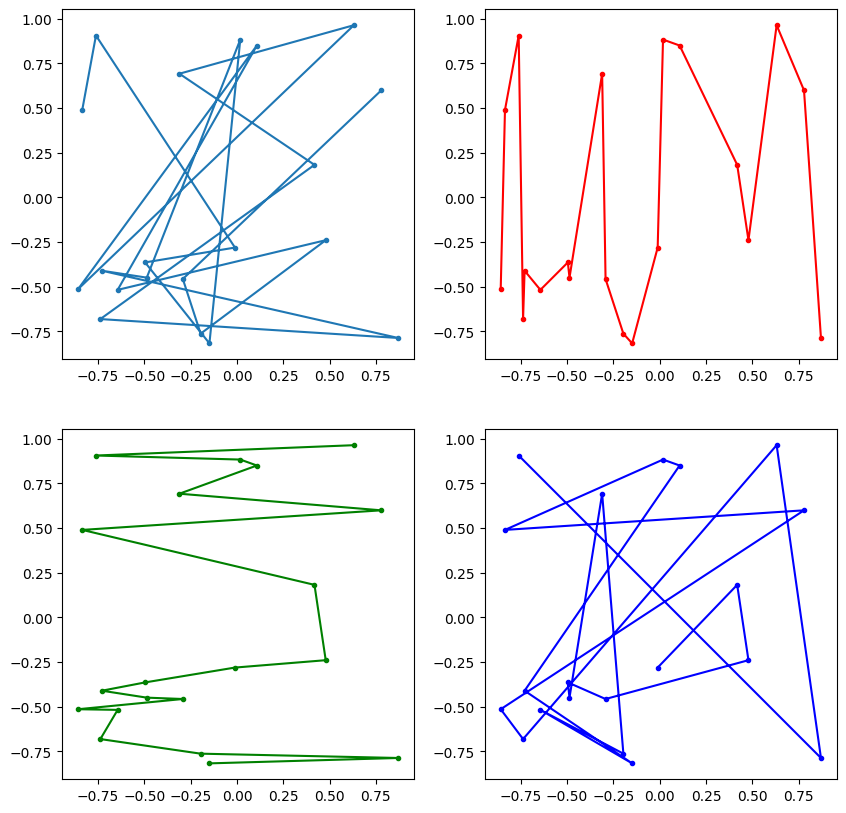
Podobně efektivní nástroj ke třídění je k dispozici v podobě standardní funkce sorted. Následující kód na příkladu náhodných komplexních čísel ukazuje, jakým způsobem můžeme určit, podle jakého klíče se mají data třídit. Složitější případy vyžadují konzultovat dokumentaci. Další zajímavost: Všimněte si strukturované varianty rozbalování (unpacking) výsledku funkce subplots.

[ ]:

import numpy as np
import matplotlib.pyplot as plt

n = 20
data1 = 2*(np.random.random(n) + 1j*np.random.random(n))-(1+1j)
data2 = sorted(data1, key=lambda z: z.real)
data3 = sorted(data1, key=lambda z: z.imag)
data4 = sorted(data1, key=lambda z: abs(z))


# protože sorted vrací seznam, pro malování konverujeme na numpy.ndarray
data2 = np.array(data2)
data3 = np.array(data3)
data4 = np.array(data4)

# čtyři obrázky v jednom
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(10,10))

ax1.plot(data1.real, data1.imag,'.-')
ax2.plot(data2.real, data2.imag,'.-r')
ax3.plot(data3.real, data3.imag,'.-g')
ax4.plot(data4.real, data4.imag,'.-b')
plt.show()

../_images/Prednaska_0110_Posledni_prednaska_31_0.png