Úvodní seznámení s matematickými programy
Integrální a diferenciální počet
Maple 12 - Integrální a diferenciální počet
| > |
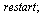 |
Limity
Limita
| > |
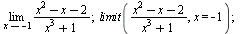 |
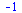 |
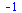 |
(6.1.1.1) |
Limita zleva
| > |
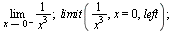 |
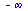 |
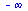 |
(6.1.2.1) |
Limita zprava
| > |
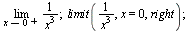 |
 |
 |
(6.1.3.1) |
Limita funkce více proměnných (navíc)
| > |
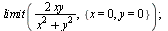 |
 |
(6.1.4.1) |
Derivace
Příkaz diff a D počítá parciální derivace.
První derivace
| > |
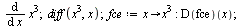 |
Vyšší derivace
| > |
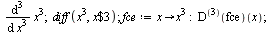 |
Derivace podle více proměnných
Integrály
Neurčitý integrál
| > |
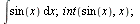 |
 |
 |
(6.3.1.1) |
Určitý integrál
| > |
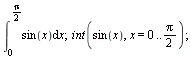 |
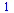 |
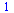 |
(6.3.2.1) |
Numerické počítání integrálů
| > |
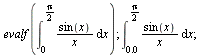 |
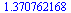 |
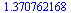 |
(6.3.3.1) |
Vícerozměrné integrály
| > |
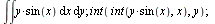 |
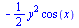 |
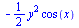 |
(6.3.4.1) |
Křivkový integrál (navíc)
| > |
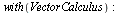 |
Délka křivky
Délka křivky, která je zadaná parametricky
| > |
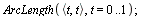 |
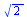 |
(6.3.5.1.1) |
Křivkový integrál I. druhu
| > |
![PathInt(y, [x, y] = Path(`<,>`(1, t), 0 .. Pi, 'coords' = 'polar')); 1](maple_files/maple_144.gif) |
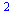 |
(6.3.5.2.1) |
Křivkový integrál II. druhu
| > |
![SetCoordinates(cartesian[x, y]); -1; LineInt(VectorField(`<,>`(y, a)), Path(`<,>`(`*`(a, `*`(cos(t))), `*`(b, `*`(sin(t)))), t = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))))); 1](maple_files/maple_146.gif)
![SetCoordinates(cartesian[x, y]); -1; LineInt(VectorField(`<,>`(y, a)), Path(`<,>`(`*`(a, `*`(cos(t))), `*`(b, `*`(sin(t)))), t = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))))); 1](maple_files/maple_147.gif) |
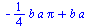 |
(6.3.5.3.1) |
Plošný integrál (navíc)
Plošný integrál I. druhu
| > |
![SetCoordinates(cartesian[x, y, z]); -1; SurfaceInt(1, [x, y, z] = Sphere(`<,>`(0, 0, 0), r)); 1](maple_files/maple_149.gif) |
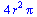 |
(6.3.6.1.1) |
Plošný integrál II. druhu
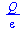 |
(6.3.6.2.1) |
Taylorův rozvoj řady
| > |
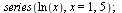 |
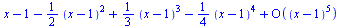 |
(6.4.1) |
| > |
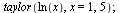 |
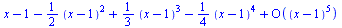 |
(6.4.2) |
Obecný tvar řady (navíc)
| > |
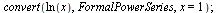 |
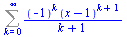 |
(6.4.1.1) |
Diferenciální rovnice
Diferenciální rovnice
| > |
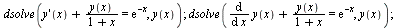 |
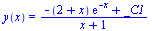 |
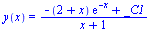 |
(6.5.1.1) |
Diferenciální rovnice s okrajovými podmínkami
| > |
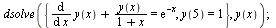 |
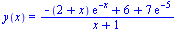 |
(6.5.2.1) |
Numerické řešení differenciálních rovnic
| > |
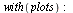 |
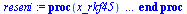 |
(6.5.3.1) |
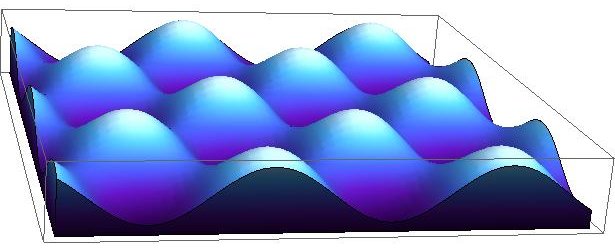
| > |
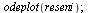 |


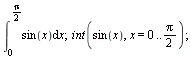
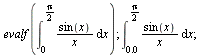
![int(int(`*`(y, `*`(sin(x))), x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi)))), y = 0 .. 1); 1; int(`*`(y, `*`(sin(x))), [x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))), y = 0 .. 1]); 1; int(int(`*`(y, `*`(sin(x))), x = ...](maple_files/maple_135.gif)