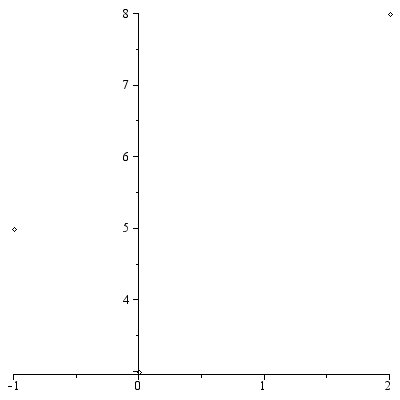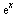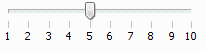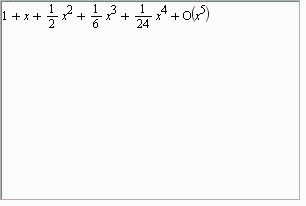Úvodní seznámení s matematickými programy
Základy používání programu
Maple 12 - Základy používání programu
Maple 12 umožňuje pracovat v rámci programu ve dvou prostředích - Worksheet mode a Document mode. Worksheet mode má výhodu, že rozlišuje mezi částmi s kódem programu, který provádí výpočty a textem, tudíž je pro začátečníka přehlednější. Document mode je
na druhou stranu mnohem komplexnější a umožňuje provádět výpočty přímo v textu, případně na jednom řádku mocí CTRL +=.
Pro práci s programem Maple se dají využít 3 základní koncepty práce. První je psaní kódu, který provádí výpočty. Druhý je pro práci využívat šablony z palet na levé straně a poslední variantou je využít pravé tlačítko myši. To v Worksheet mode po zvolení příslušného příkazu generuje kód, v Document mode provádí výpočet na řádku za pomoci šipky.
Níže budeme pracovat ve Worksheet modu a budeme především využívat možnost psaní kódu, případně využívat šablon.
Použití pravého tlačítka myši je zmiňováno pouze u grafů, dá se ale vyžít při řešení rovnic, zjednodušování výrazů, v integrálním a diferenciálním počtu atd.. Důvodem je, že čtenář nepozná rozdíl (ve Worksheet mode), byl-li příslušný příkaz napsán ručně, případně vygenerován za pomocí pravého tlačítka myši.
Výpočty ukončujeme středníkem (není nutné pro jeden výpočet v jedné sekci označené
>).
Enter provede výpočet.
Shift + Enter posune na další řádek.
Tlačítko
na horní liště přeruší výpočet.
Výpočty jsou prováděny v časovém pořadí v jakém jste spustili výpočty. Je tedy možné přiradit nějakou proměnnou na konci worksheetu a pokud poté provede s proměnnou výpočet např. na počátku, tak již bude program počítat s vaší zadanou hodnotou proměné.
Pokud chcete nechat propočítat celý pracovní list, kliknětě na tlačítko
v horní liště, případně v nabídce Edit/Execute/Worksheet.
Pokud výpočet ukončíme dvojtečkou výpočet se provede, ale nevypíše.
Pro většinu složitějších funkcí je nutné zavolat balíčky příkazem with např. with(plots). Případně se dají balíčky zavolat v menu Tools záložka Load Package.
Pokud kliknete na danou funkci a stiknete klávesu F2, zobrazí se k dané funkci nápověda. Alternativně se nápověda zobrazí pokud před danou funkci napíšete otazník.
Pro zápis příkazů je možné využít jak příkazy x^2, int(sin(x),x), tak případně šablony v paletách na levé straně.
Příkazy typu x^2 a podíly se automaticky převádějí na šablony již při psaní.
Hodí se na počátku pracovního listu použít příkaz restart. Jednak se tím odstraní přiřazení proměnných a také načtené balíčky. Předejde se tím např. zavolání funkce z balíčku ještě před jeho načtením.
Pro práci s programem doporučuji požívat anglickou klávesnici, jelikož se snadněji zadávají např. složené závorky ({}), mocniny (^) apod..
Taktéž se hodí nastavit vyhlazování písma v Tools/Options/Display položka Font anti-aliasing na Enabled. Písmo pak nebude tak "kostičkované".
Pozor! Funkce evalf pro malý počet cifer může dát nepřesný výsledek. Je lepší pro číselnou hodnotu neprve provést příkaz evalf a poté na výsledek použít např. evalf[2], který zaokrouhlí na 2 platné číslice.
Pozor! Standartně je ve vzhledu stránky (File/Page setup) nastaven jako typ papíru Letter. Pro tisk je potřeba jej nastavit na A4.
Má-li program nějaké speciální funkce vůči ostatním je za příslušným názvem odstavce "(navíc)".
| > |
 |
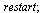Základní operace
Maple 12 - Základní operace
Základní matematické operace
Základní operace +-*/ se používají stejně jako v jakémkoli jiném programovacím jazyku. U dělení je dobré si dát pozor, aby složitější výrazy byly v závorkách, jejikož dělení má přednost před sčítáním. Poslední provedený výpočet se zavolá %.
| > |
 |
 |
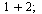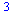(2.1.1) |
| > |
 |
 |
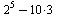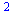(2.1.2) |
| > |
 |
 |
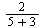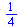(2.1.3) |
Číselný výpočet
U definovaných funkcí a zlomků se výrazy automaticky nepřevádějí na číselnou hodnotu (z důvodu přesnosti). Pokud ale je nějaké z čísel je desetiné, dostaneme číselnou hodnotu, ne zlomek (což se dá využít i jako trik, pro rychlé získání číselné hodnoty).
| > |
 |
 |
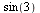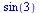(2.2.1) |
| > |
 |
 |
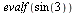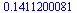(2.2.2) |
| > |
)](maple_files/maple_14.gif) |
 |
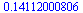(2.2.3) |
Trik
| > |
 |
 |
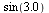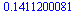(2.2.1.1) |
Matematické konstanty
Matematické konstanty můžeme napsat pomocí klávesnice s velkým písmenem na počátku (neplatí pro Eulerovo číslo e - to je možné napsat jako exp(1) a nekonečno), případně je možné využít opět nakliknutí příslušné konstanty pomocí palety. U nekonečna je možné pracovat s různými typy nekonečna (viz. nápověda).
| > |
 |
| > |
 |
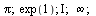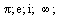Definování proměnné
U definování názvů proměnné se hodí nepoužívat háčky a čárky, případně speciální znaky.
| > |
 |
 |
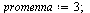(2.4.1) |
| > |
 |
 |
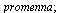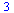(2.4.2) |
Definování vlastní funkce
| > |
 |
 |
 |
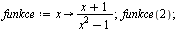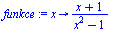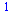(2.5.1) |
Definovaní funkce pokud je výraz funkce v jiné proměnné.
| > |
 |
 |
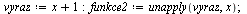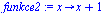(2.5.2) |
Řešení rovnic a nerovnic
Maple 12 - Řešení rovnic a nerovnic
Řešení rovnice
| > |
 |
 |
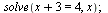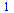(3.1.1) |
| > |
 |
 |
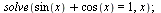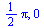(3.1.2) |
| > |
 |
 |
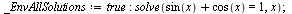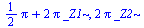(3.1.3) |
Řešení soustavy rovnic
| > |
![solve({`+`(x, `-`(y)) = 2, `+`(x, y) = 1}, [x, y]); 1](maple_files/maple_43.gif) |
![[[x = `/`(3, 2), y = -`/`(1, 2)]]](maple_files/maple_44.gif) |
(3.2.1) |
Řešení nerovnice
| > |
 |
 |
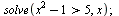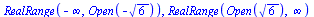(3.3.1) |
Řešení rovnice s podmínkami
| > |
 |
 |
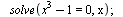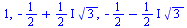(3.4.1) |
| > |
 |
 |
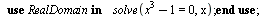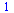(3.4.2) |
| > |
![solve([`+`(`*`(`^`(x, 2)), x, `-`(6)) = 0, `>`(x, 0)], x); 1](maple_files/maple_51.gif) |
 |
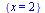(3.4.3) |
Úprava výrazů
Maple 12 - Úprava výrazů
Zjednodušení výrazu
| > |
 |
 |
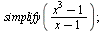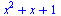(4.1.1) |
Rozklad výrazu
| > |
 |
 |
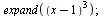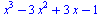(4.2.1) |
Složení výrazu
| > |
 |
 |
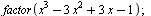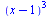(4.3.1) |
Převedení na společného jmenovate
| > |
 |
 |
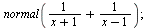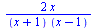(4.4.1) |
| > |
 |
 |
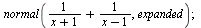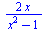(4.4.2) |
Rozklad na parciální zlomky
| > |
 |
 |
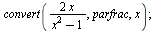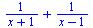(4.5.1) |
Vektory a matice
Maple 12 - Vektory a matice
Pro práci s vektory a maticemi budeme pro některé funkce potřebovat balíček Lineární algebry a balíček pro práci s vektory. Ve starších verzích programu Maple se používal balíček linalg, který stále funguje, ale už se nedoporučuje jej používat.
| > |
 |
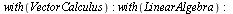Vektory
Zápis vektoru
Zápis pomocí lomených závorek (<>), je snadnější, ale zapisuje vektor ve sloupcovém tvaru.
| > |
![`:=`(vektor, Vector([3, 1, 2])); 1; `<,>`(3, 1, 2); 1](maple_files/maple_66.gif) |
](maple_files/maple_67.gif) |
](maple_files/maple_68.gif) |
(5.1.1.1) |
Složky vektoru
| > |
![vektor[1]; 1; vektor[1]; 1](maple_files/maple_69.gif) |
 |
 |
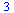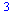(5.1.2.1) |
Velikost vektoru
| > |
 |
 |
 |
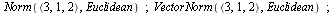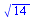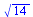(5.1.3.1) |
Skalární součin
| > |
 |
 |
 |
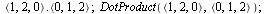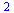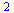(5.1.4.1) |
Vektorový součin
| > |
 |
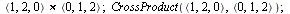![`+`(`*`(4, `*`(e[x])), `-`(`*`(2, `*`(e[y]))), e[z])](maple_files/maple_79.gif) |
](maple_files/maple_80.gif) |
(5.1.5.1) |
Matice
Zápis matice
Jelikož zápis pomocí složených závorek zapisuje vektor ve sloupcovém tvaru, je nutné následně matici transponovat.
| > |
![`:=`(matice, Matrix([[1, 2], [3, 1]])); 1; Transpose(`<|>`(`<,>`(1, 2), `<,>`(3, 1))); 1](maple_files/maple_81.gif) |
 |
 |
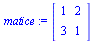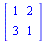(5.2.1.1) |
Zápis matice II - pomocí palety matrix
| > |
 |
 |
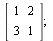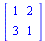(5.2.2.1) |
Složky matice
| > |
![matice[1, 2]; 1; matice[1, 2]; 1](maple_files/maple_86.gif) |
 |
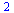(5.2.3.1) |
|
|
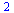Determinant matice
| > |
 |
 |
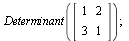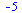(5.2.4.1) |
Vlastní čísla
| > |
 |
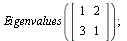](maple_files/maple_91.gif) |
(5.2.5.1) |
Integrální a diferenciální počet
Maple 12 - Integrální a diferenciální počet
| > |
 |
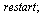Limity
Limita
| > |
 |
 |
 |
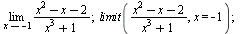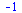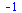(6.1.1.1) |
Limita zleva
| > |
 |
 |
 |
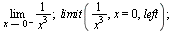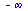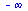(6.1.2.1) |
Limita zprava
| > |
 |
 |
 |
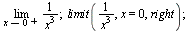(6.1.3.1) |
Limita funkce více proměnných (navíc)
| > |
 |
 |
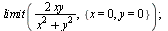(6.1.4.1) |
Derivace
Příkaz diff a D počítá parciální derivace.
První derivace
| > |
 |
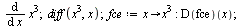Vyšší derivace
| > |
 |
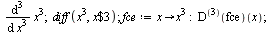Derivace podle více proměnných
Integrály
Neurčitý integrál
| > |
 |
 |
 |
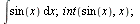(6.3.1.1) |
Určitý integrál
| > |
 |
 |
 |
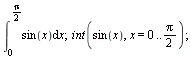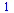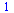(6.3.2.1) |
Numerické počítání integrálů
| > |
 |
 |
 |
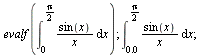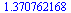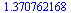(6.3.3.1) |
Vícerozměrné integrály
| > |
 |
 |
 |
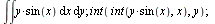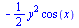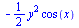(6.3.4.1) |
Křivkový integrál (navíc)
| > |
 |
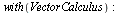Délka křivky
Délka křivky, která je zadaná parametricky
| > |
 |
 |
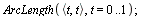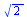(6.3.5.1.1) |
Křivkový integrál I. druhu
| > |
![PathInt(y, [x, y] = Path(`<,>`(1, t), 0 .. Pi, 'coords' = 'polar')); 1](maple_files/maple_144.gif) |
 |
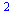(6.3.5.2.1) |
Křivkový integrál II. druhu
| > |
![SetCoordinates(cartesian[x, y]); -1; LineInt(VectorField(`<,>`(y, a)), Path(`<,>`(`*`(a, `*`(cos(t))), `*`(b, `*`(sin(t)))), t = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))))); 1](maple_files/maple_146.gif)
![SetCoordinates(cartesian[x, y]); -1; LineInt(VectorField(`<,>`(y, a)), Path(`<,>`(`*`(a, `*`(cos(t))), `*`(b, `*`(sin(t)))), t = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))))); 1](maple_files/maple_147.gif) |
 |
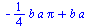(6.3.5.3.1) |
Plošný integrál (navíc)
Plošný integrál I. druhu
| > |
![SetCoordinates(cartesian[x, y, z]); -1; SurfaceInt(1, [x, y, z] = Sphere(`<,>`(0, 0, 0), r)); 1](maple_files/maple_149.gif) |
 |
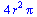(6.3.6.1.1) |
Plošný integrál II. druhu
 |
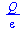(6.3.6.2.1) |
Taylorův rozvoj řady
| > |
 |
 |
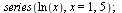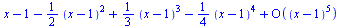(6.4.1) |
| > |
 |
 |
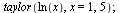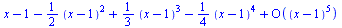(6.4.2) |
Obecný tvar řady (navíc)
| > |
 |
 |
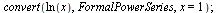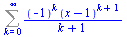(6.4.1.1) |
Diferenciální rovnice
Diferenciální rovnice
| > |
 |
 |
 |
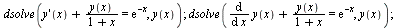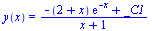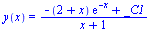(6.5.1.1) |
Diferenciální rovnice s okrajovými podmínkami
| > |
 |
 |
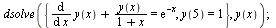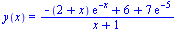(6.5.2.1) |
Numerické řešení differenciálních rovnic
| > |
 |
 |
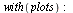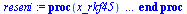(6.5.3.1) |
| > |
 |
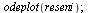Posloupnosti a řady
Maple 12 - Posloupnosti a řady
Posloupnosti
| > |
 |
 |
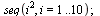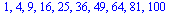(7.1.1) |
Řady
| > |
 |
 |
 |
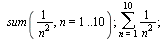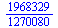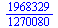(7.2.1) |
| > |
 |
 |
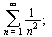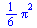(7.2.2) |
Grafy 2D a 3D
Maple 12 - Grafy 2D a 3D
Maple umožnuje vytvoření grafů různým způsobem. Pro rychlé vytvoření grafu z daného výrazu (např. sin(x) se dá využít pravé tlačítko myši - kliknutím na výraz a poté z nabídky Plots vybrat typ grafu, který chceme vytvořit.
Další variantou je využít Plot Builder z nabídky Tools/Assistans.
Taktéž se dá graf vytvořit jen vložením prostředím pro grafy v nabídce Insert-Plot a následným přetažením výrazu do tohoto prosředí.
Poslední variantou je vytvoření grafu pomocí příkazů typu plot, která umožňuje měnit vzhled grafu za pomocí jednotlivých příkazů.
Vzhled grafu se dá měnit kliknutím pravým tlačítkem na graf, ale pokud byl graf vytvořen pomocí příkazů (smartplot, plot...), tak se takto provedené změny ztratí.
| > |
 |
| > |
 |
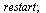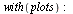Grafy 2D
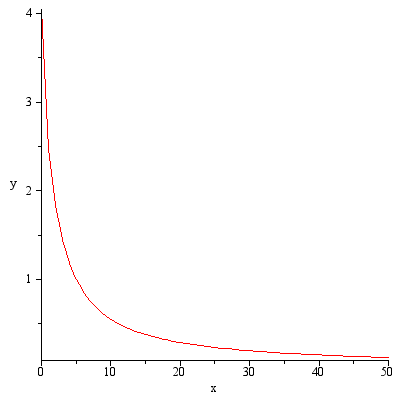
Graf x,y
| > |
 |
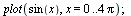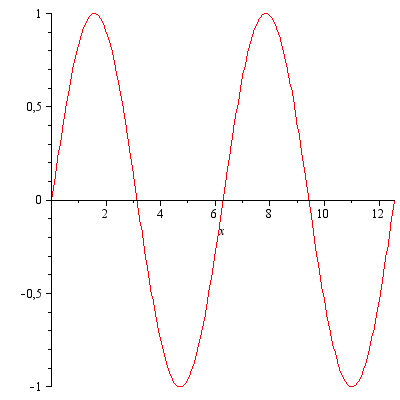
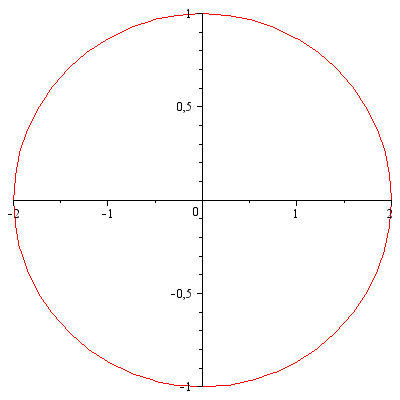
Parametrický graf
| > |
![plot([`+`(`*`(2, `*`(sin(t)))), cos(t), t = 0 .. `+`(`*`(2, `*`(Pi)))]); 1](maple_files/maple_184.gif) |
Graf na zobrazení dat
| > |
![pointplot([[0, 3], [2, 8], [-1, 5]]); 1](maple_files/maple_186.gif) |
Grafy 3D
Graf x,y,z
| > |
 |
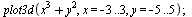Parametrický graf - křivka
| > |
![spacecurve([sin(t), t, t], t = -10 .. 10); 1](maple_files/maple_190.gif) |
Parametrický graf - plocha
| > |
![plot3d([`*`(u, `*`(sin(t))), `*`(t, `*`(`^`(u, 2))), `*`(t, `*`(u))], t = -5 .. 5, u = -2.5 .. 2.5); 1](maple_files/maple_192.gif) |
Zobrazení více typů grafů v jednom
Fyzikální jednotky
Maple 12 - Fyzikální jednotky
Maple umožňuje používat u proměnných fyzikální jednotky. Pro práci s nimi je potřeba zavolat balík Units. Jednotky se dají napsat pomocí funkce Unit, elegantnější spůsob je nakliknout jednotku přímo z palety Units (SI). Pro zjednodušení jednotek funguje příkaz simplify.
| > |
 |
| > |
 |
 |
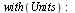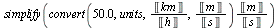(8.4.1) |
| > |
 |
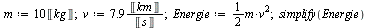Zajímavosti pro učitele
Maple 12 - Zajímavosti pro učitele
Interaktivní změna dokumentu
Interaktivní změny v dokumentu se dělají pomocí palety Components. Způsob výroby takové části materiálu je složitější, doporučuji si projít nápovědu s daným tématem - "Smart1, Tour".
Pokud chcete jen prozkoumat jak se danný problém chová pro různé parametry, je možné použít příkaz Explore, případně jen kliknout pravým tlačítkem na danný výraz s proměnnými a zvolit v nabídce explore. Bude poté dotázáni, pro které parametry chcete problém zkoumat a v jakých mezích (pokud některou proměnnou chcete vynechat, zašktněte u ní políčko skip. Po potvrzení se vám v novém okně automaticky vytvoří pole které se interaktivně mění (graf, případně rám, ve kterém se vám mění funkce) a táhla pro proměnné.
Graf funkce sin(a⋅x)
| > |
 |
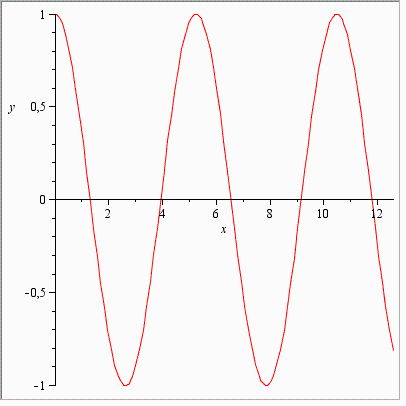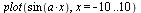
Taylorův rozvoj funkce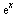 
| > |
  |
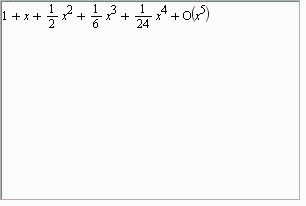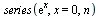
Záložka Tools
Rozhodně stojí zato si projít v záložce Tools záložku Tutors. Je zde možné např. nechat si vypočítat limity případně integrály i s postupem.
Maplet
Je možné vytvořit Maplet - prostředí podobné Java apletům a spouštět jej za pomocí programu Maplet Viewer. Případně je možné vyrobit Maplet pomocí Maplet Builderu v záložce Tools/Assistant.
Převedení na html
Worksheet je možné převést na html stránku. Export se neprovede pokud je někde v dokumentu vložen konec stránky (Insert/Page Break).
Převedení do LaTeXu
Je možné převést jen určitý výraz příkazem latex, případně převést celý dokument
za pomocí File/Export as.
Při exportu celého souboru se musí do stejného adresáře nakopírovat soubory ze složky Maple 12/ETC, jinak se soubor nedá zpracovat. Taktéž se musí do příslušného souboru zadat jaký typ kódování byl použit, jinak se nezobrazí háčky a čárky. I přes to všechno soubor obsahuje chyby při zpracování LaTeXem.
Převedení na formát rtf
Je možné převést celý dokument na formát rtf za pomocí File/Save as. Celkově ale vypadá mnohem lépe, než export do LaTeXu.
Závěrečné shrnutí
Maple 12 - Závěrečné shrnutí
Výše nastíněné funkce jsou jen základní funkce programu, které by měl student znát, pro snadnější práci s programem během studia. Samozřejmě, že Maple nabízí mnohem více funkcí. Mnoho funkcí jako např. plot, případně solve mají množství nastavení, které můžeme nastavit tak, aby výsledek odpovídal našemu očekávání (např. změnit vzhled grafu, případně nastavit podmínky pro řešené rovnice).
Doporučená literatura
Maple 12 - Doporučená literatura
Abell M. L., Braselton J. P.: Maple by example, 3rd edition, Elsevier, 2005
Shingareva I., Lizárraga-Celaya C., Braselton J. P.: Maple and Mathematica, Springer, 2007
Wang F. Y.: Physics with Maple, Wiley-VCH Verlag GmbH, 2005
Odkazy
Maple 12 - Odkazy
http://www.maplesoft.com/
http://www.maplesoft.com/products/Maple/index.aspx
http://www.maplesoft.com/applications/index.aspx
http://www.maplesoft.com/support/training/index.aspx
http://www.maplesoft.com/TeacherResource/
http://www.maplesoft.com/products/maplesim/index.aspx
Soubory ke stažení
Maple 12 - Soubory ke stažení
Úvodní seznámení ve formátu pdf a formátu programu Maple 12 (mw) je možné stáhnout
zde.
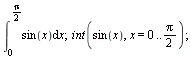
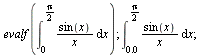
![int(int(`*`(y, `*`(sin(x))), x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi)))), y = 0 .. 1); 1; int(`*`(y, `*`(sin(x))), [x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))), y = 0 .. 1]); 1; int(int(`*`(y, `*`(sin(x))), x = ...](maple_files/maple_135.gif)
![int(int(`*`(y, `*`(sin(x))), x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi)))), y = 0 .. 1); 1; int(`*`(y, `*`(sin(x))), [x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))), y = 0 .. 1]); 1; int(int(`*`(y, `*`(sin(x))), x = ...](maple_files/maple_136.gif){kind=small}
![int(int(`*`(y, `*`(sin(x))), x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi)))), y = 0 .. 1); 1; int(`*`(y, `*`(sin(x))), [x = 0 .. `+`(`*`(`/`(1, 2), `*`(Pi))), y = 0 .. 1]); 1; int(int(`*`(y, `*`(sin(x))), x = ...](maple_files/maple_137.gif){kind=small}
![assume(`::`(R, real), `>`(R, 0)); -1; SetCoordinates(spherical[r, phi, theta]); -1; Flux(VectorField(`<,>`(`*`(Q, `*`(`/`(`+`(`*`(4, `*`(Pi, `*`(epsilon, `*`(`^`(r, 2))))))))), 0, 0)), Sphere(`<,>`(0,...](maple_files/maple_151.gif){kind=small}
![assume(`::`(R, real), `>`(R, 0)); -1; SetCoordinates(spherical[r, phi, theta]); -1; Flux(VectorField(`<,>`(`*`(Q, `*`(`/`(`+`(`*`(4, `*`(Pi, `*`(epsilon, `*`(`^`(r, 2))))))))), 0, 0)), Sphere(`<,>`(0,...](maple_files/maple_152.gif){kind=small}
![assume(`::`(R, real), `>`(R, 0)); -1; SetCoordinates(spherical[r, phi, theta]); -1; Flux(VectorField(`<,>`(`*`(Q, `*`(`/`(`+`(`*`(4, `*`(Pi, `*`(epsilon, `*`(`^`(r, 2))))))))), 0, 0)), Sphere(`<,>`(0,...](maple_files/maple_153.gif){kind=small}
![`:=`(p1, plot3d(`+`(`*`(`^`(x, 3)), `*`(`^`(y, 2))), x = -3 .. 3, y = -5 .. 5, color = 'red')); -1; `:=`(p2, plot3d([sin(t), cos(t), u], t = 0 .. `+`(`*`(2, `*`(Pi))), u = -50 .. 50, color = 'blue'));...](maple_files/maple_194.gif){kind=small}
![`:=`(p1, plot3d(`+`(`*`(`^`(x, 3)), `*`(`^`(y, 2))), x = -3 .. 3, y = -5 .. 5, color = 'red')); -1; `:=`(p2, plot3d([sin(t), cos(t), u], t = 0 .. `+`(`*`(2, `*`(Pi))), u = -50 .. 50, color = 'blue'));...](maple_files/maple_195.gif){kind=small}
![`:=`(p1, plot3d(`+`(`*`(`^`(x, 3)), `*`(`^`(y, 2))), x = -3 .. 3, y = -5 .. 5, color = 'red')); -1; `:=`(p2, plot3d([sin(t), cos(t), u], t = 0 .. `+`(`*`(2, `*`(Pi))), u = -50 .. 50, color = 'blue'));...](maple_files/maple_196.gif){kind=small}
