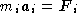
Na obdobné téma jsem hovořil na několika seminářích organizovaných profesorem Černohorským. Diskusím na nich i osobním diskusím s profesorem Černohorským vděčím za to, že jsem si řadu věcí ujasnil a tak se mi snad zde podaří shrnout problematiku výstižným způsobem.
Každý fyzik či matematik bude asi v prvním okamžiku souhlasit s tím, že tento požadavek musí být splněn při budování pojmové struktury čehokoli, co se chce hlásit k názvu "věda" a mělo by být naplňováno i v politice a každodenních diskusích. V následující chvíli si však uvědomí, že je to logicky nemožné, pokud pod pojmem "definice" rozumíme deskriptivní definici, tedy výrok, ve kterém definovaný pojem, definiendum, je vysvětlen pomocí výrazu, definiens, vytvořeného z jiných pojmů. Výkladový slovník jazyka českého, založený právě na takovýchto definicích, nám dobře poslouží, nevíme-li např. co je to okrápka; dozvíme se, že je to "rám zachycující u povozu bláto". (Než jsem otevřel Trávníčka, abych nalezl příklad, tak jsem to také nevěděl; MS Word pod tím udělal červenou vlnovku a nabízel slovo "odkrápka", což opět podle Trávníčka je "přikrývka nad kočárem zachycující déšť " -- to uvádím proto, aby čtenář, kterému zbytek článku bude připadat nezajímavý či triviální, se dozvěděl alespoň něco poučného.) Tentýž slovník nám ovšem řekne, že otec = rodič a rodič = otec, rodiče = otec a matka. Ať se snažíme sebevíce, takovéto deskriptivní definice se nám vždy uzavřou do kruhu, nebo nám v celém systému zbudou určité primitivní pojmy, které zůstanou nedefinovány.
Příklad z oblasti jazyka je pro náš účel zajímavý ze dvou důvodů. Předně se zdá na první pohled nepochopitelné, jak jsme se mohli vůbec naučit mluvit, když jsme přišli na svět s nulovou slovní zásobou; faktem ale je, že jsme se to nějak naučili.
První substantiva jsme se naučili ostentativní definicí, tj. někdo nám ukázal, že toto je otec, jak jsme se ale naučili správně užívat pojmy jako "krásný" nebo "přemýšlení"? Později budu argumentovat, že problém není tak odtažitý od problému definice fyzikálních veličin, jak se na první pohled může zdát.
Druhým důvodem je, že i když bez detailnějšího rozboru chápeme, že heslo v nadpise není tak snadné naplnit, nejsme asi ochotni připustit, že je to omluva pro výroky, které postrádají jasný obsah. Jsme jistě přesvědčeni, že pojmy užívané ve vědecké řeči dobře definované jsou, i když všechny nemohou být definovány deskriptivně. Jak jsou vlastně definovány by měl naznačit tento článek.
Zmíněný problém vystupuje samozřejmě i v čisté matematice a je řešen axiomatickou metodou. Bod a přímka jsou v euklidovské axiomatice primitivní pojmy, které zůstanou nedefinovány, resp. nejsou definovány explicite.
Pojem vektoru je primitivním pojmem v teorii vektorových prostorů nad tělesem reálných či komplexních čísel. Nezáleží na tom, že idea vektorového prostoru vznikla z fyziky či geometrie (lat. vector značí někoho, co něco přenáší, termín má tedy jasný geometrický původ), ve formalizované teorii je to prostě prvek vektorového prostoru, který je definován určitou soustavou axiomů o sčítání vektorů a násobení vektorů číslem. Orientované úsečky v euklidovském prostoru, n-tice reálných čísel s určitými pravidly sčítání a násobení číslem, matice určitého řádu či lebesqueovsky integrovatelné funkce na intervalu představují určité modely vektorového prostoru. Nicméně v těchto modelech nám axiomy implicite definují, co vektory jsou, řada autorů proto mluví o axiomech jako implicitních definicích. Mějme ale na paměti jednu věc - nemá smysl se izolovaně ptát, zda n-tice reálných čísel , matice k-tého stupně či orientovaná úsečka je vektor - musíme zároveň brát v potaz pravidla pro jejich sčítání a násobení a ptát se, zda vyhovují požadavkům axiomů vektorového prostoru.
Problém formální struktury a obsahu fyzikálních zákonů se rozebírá ve velké řadě knih. Uvádím z nich jen několik: [1-6]. Většina autorů buď ve fyzice či matematice aktivně pracovala, nebo měla alespoň dobré fyzikální vzdělání, takže hovořila opravdu o reálných problémech, které ve fyzice vystupují. V detailech se ovšem přístup jednotlivých autorů liší.
Následující charakteristika matematické a fyzikální teorie nemusí být všeobecně přijata, v zásadě však vystihuje, jak se tyto pojmy v současnosti chápou.
Matematická teorie je dána souborem bezesporných axiomů a syntaktických pravidel, pomocí kterých se tvoří z axiomů věty.
Fyzikální teorie má též obě tyto složky. Úlohu axiomů hrají "principy" či "postuláty" (a samozřejmě axiomy matematické teorie, která je v ní užita). Terminologie je zde nejednotná, z historických důvodů jsou některé postuláty označovány jako "zákony "(Newtonovy zákony) či "věty" (I až III věta termodynamická), vhodnější je ale jako zákony označovat důsledky postulátů, tedy analogii matematických vět.
Fyzikální teorie má však ještě něco navíc -- sémantická pravidla, která přiřazují pojmům teorie pozorovatelné veličiny, díky kterým můžeme teorii interpretovat jako teorii hovořící o světě kolem nás. Soustředíme se na tuto poslední část, která nese sebou řadu problémů různého charakteru.
Nejpřímočařeji přistupuje k problému operacionalizmus, jehož nejvýznamnějším představitelem je laureát Nobelovy ceny za fyziku P.W.Bridgman. Fyzikální veličina je podle něj definována způsobem, jakým je měřena. (Obdobné operacionalistické definice jsou pak vyžadovány i v ostatních vědách i v celé teorii poznání [2].) Vzdálenost dvou bodů tedy např. znamená, kolikrát jsme přiložili podél přímky spojující dva body standard délky, náboj je definován způsobem svého měření atd.
Proti takto formulované myšlence lze namítnout, že příslušnou veličinu lze měřit různými způsoby. Například základní jednotka délky dnes již není definována pomocí tuhého standardu, nýbrž prostřednictví rychlosti světla a času. Hovoříme-li o určité fyzikální veličině, máme na mysli něco abstraktnějšího, než pouhý výsledek určitého postupu měření. Takto naivně však neformulují svůj přístup ani operacionalisté, nepůjdeme zde však do detailů operacionalistického přístupu a jeho kritiky. Zdůrazníme však, co je hlavním cílem operacionalizmu, ve kterém se neliší od filosofů vědy, které lze přiřadit ke směru, který B.Russell [7] nazývá "školou logické analýzy" a jejímž současným pokračovatelem je analytická filosofie: odstranit z vědy (a jazyka vůbec) zdánlivé definice, které jsou ve skutečnosti bezobsažné. Sem patří výroky jako "prostor a čas jsou formou existence hmoty", ale i "síla je příčinou pohybu". Veličina musí být určena tak, abychom věděli, jaké číselné hodnoty máme dosadit do příslušných rovnic, vyjadřujících určitý fyzikální vztah. Návod, podle kterého můžeme veličiny takto určit budu nazývat operacionalistickou definicí, jež může být ale chápána v širším než bridgmenovském smyslu.
Všimněme si však základního problému, který interpretace určité teorie představuje: čemu vlastně jsou přiřazeny pojmy teorie? Chceme odpovědět tak, že "realitě", zde však narazíme na potíž. Nemám na mysli filosofické problémy po berkleyovské linii, že to, co analyzujeme jsou vlastně naše počitky. Všechna fyzikální měření se nakonec redukují na vztahy mezi makroskopickými objekty a výrok, že ručička přístroje ukazuje na určitou rysku nepředstavuje menší, ale také ne větší problém, než výrok že na stole leží sklenice, můžeme ho tedy interpretovat v duchu naivního realismu, v rámci kterého se úspěšně orientujeme v každodenním životě. Filosof by jistě namítl, že jsem se jeho námitkám (netvrdím že neoprávněným) vyhnul příliš snadno. Chci zdůraznit, že se snažím jen zmapovat, jak se ve fyzice skutečně postupuje a diskusi o tom, proč tento postup vede k nesporným praktickým úspěchům, nechávám stranou.
Mám na mysli něco jiného. Užitečným teoretickým konceptem je např. hmotný bod. Jenže hmotný bod v přírodě nenajdeme. Jakmile řekneme, že hmotný bod je malé tělísko, dostáváme model, který funguje v řadě situací, ale nefunguje v jiných.
Navíc, žádná teorie, kterou máme k dispozici, není úplnou teorií. I pokud by byla např. teorie strun hledanou finální "teorií všeho", nebude nám moc platná k vybudování pojmů, užívaných řekněme v teorii pevných látek. Nikdo neumí skutečně vybudovat teorii jádra ze standardního modelu, i když máme dobré důvody věřit, že z něho určitým způsobem vyplývá, natož pak teorii krystalu. Z obdobných důvodu je neschůdná snaha redukovat pojem makroskopické síly na něco vyjádřitelného pomocí čtyř základních interakcí, i když máme dobré důvody věřit, že na fundamentální úrovni jiné interakce neexistují. Na řadě dalších úrovní je určitá fenomenologie nezbytná.
Situace je vlastně taková, že pojmům určité konsistentní teorie (např. maxwellovské elektrodynamiky) přiřazujeme veličiny v jakémsi modelu reality a druhým krokem je, že posuzujeme, ať už experimentálně, nebo na základě úplnější teorie (např. kvantové elektrodynamiky) nakolik se tento model shoduje se "skutečnou" realitou. V následujícím ukáži na jednoduchém modelu, jakým způsobem představují fyzikální principy implicitní definice veličin, které v nich vystupují.
Představme si jednoduchý model v rámci newtonovské mechaniky. Předpokládejme, že máme systém N hmotných bodů, interagujících pouze elektrostaticky. Jejich pohyb je tedy určen zákonem (v rámci daného modelu postulátem):
Každému hmotnému bodu jsou přiřazeny dvě konstanty mi a qi, specifické pro daný i-tý bod, kterým říkáme hmotnost a náboj. Pohyb této soustavy hmotných bodů vzhledem k vztažnému systému, kterému říkáme inerciální, je pak určen vztahy:
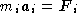 |
(1) |
kde
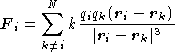 |
(2) |
a k je daná konstanta.
Na počátku máme tedy v naší teorii 2N neznámých parametrů mi a qi a nevíme, co je to inerciální systém (pokud bych se pokoušel o důslednější axiomatiku, musel bych vysvětlit i pojem "vztažný systém" a další slova, chci však však jen naznačit hlavní myšlenku).
Změříme-li nyní při různém uspořádání bodů celkem 2N složek zrychlení1 a výsledky dosadíme do vztahů, dostaneme soustavu 2N homogenních lineárních rovnic pro náboje qk a poměry hmotností ku nábojům mi/qi. Pokud tato soustava má řešení, její řešení je určeno jednoznačně až na jeden parametr, který odpovídá volbě jednotek pro jednu z veličin (jednotky pro druhou sadu veličin už jsme fixovali volbou konstanty úměrnosti k ve vztahu definujícím sílu). Pokud soustava řešení nemá, znamená to, že souřadnice bodů nemáme určeny vzhledem k inerciálnímu systému a musíme provést transformaci souřadnic a jí odpovídající transformaci zrychlení takovou, aby soustava řešení měla.
Jakmile víme, že jsme v inerciálním systému a určili jsme volné parametry, fungují naše vztahy jako pohybový zákon, který nám z počátečních podmínek umožní určit vývoj systému.
V tomto smyslu tedy náš základní postulát funguje zároveň jako pohybový zákon a zároveň jako implicitní definice hmotností, nábojů a inerciálního systému.
Abychom ale mohli naznačené operace provádět, musíme ovšem vědět, co znamená zrychlení, tedy, co znamená pojem délky a času, podle kterého derivujeme. Můžeme zavést pojem ideálních hodin a ideálních měřítek, pomocí kterých provádíme měření a potom v rámci teorie sestrojit jejich modely. Pedagogicky je to vhodný postup, představuje však jakýsi úkrok stranou. Ve skutečnosti jsou však i pojmy "délka" a "čas" implicite definovány našim pohybovým zákonem.
Řekli jsme již, jak nám náš pohybový zákon umožní rozlišit, zda jsou souřadnice bodů vztaženy k inerciálnímu nebo neinerciálnímu systému. Nejobecnější transformací, která zachovává tvar našich rovnic je, jak je dobře známo, obecná Galileiho transformace, čímž míníme transformaci mezi dvěma systémy, které se vzájemně pohybují rovnoměrně přímočaře a čas je v nich měřen tak, že oba časové údaje se liší jen o konstantu, odpovídající posunu časového počátku. Na souřadnice bodů a časové údaje se tedy můžeme na počátku dívat jen jako na značky přiřazené událostem. Jen při určitých hodnotách těchto značek (tedy jen s volností, kterou poskytuje Galileiho transformace), se budou naše měření shodovat s předpovědí teorie (o které zde předpokládáme, že v našem modelu je správnou teorií). Budeme-li např. používat špatně jdoucích hodin, pak zjistíme, že teorie není ve shodě s pozorováním a budeme hodiny korigovat tak dlouho, až ke shodě dojde. (Pokud se nám nepovede dojít naznačenými způsoby ke shodě, musíme konstatovat, že teorie je nesprávná. Zde nás však zajímala jen otázka implicitní definice jednotek, proto jsme předpokládali, že teorie platí. Reálně bychom zjistili, že náš postup vede k cíli, pokud hmotné body modelujeme malými nabitými kuličkami, jejichž vzdálenosti jsou velké vzhledem k jejich rozměrům a jejich rychlosti a zrychlení jsou malé, takže se neuplatňují magnetické síly a efekty záření. Obdobná implicitní definice pojmů maxwellovské elektrodynamiky se dikutuje v [1].)
Definice času samozřejmě nebude mít nikdy tvar deskriptivní definice tvaru "Čas je ...". Spíše vlastně odpovídá klasické parodii špatné odpovědi "Čas je když..." Slovně ji můžeme formulovat: V rámci určité teorie existuje taková proměnná, které říkáme čas, a existují takové konstanty (v našem případě náboje a hmotnosti) a proměnné (v našem případě prostorové souřadnice), že platí ..." , kde za tečky musíme dosadit vyjádření základního zákona.
Všimněme si ještě jedné skutečnosti. Obecně nelze nejdříve vybudovat metateorii prostoru a času a pak v ní formulovat pohybové zákony. Veličiny teorie jsou definovány implicite celou sítí vztahů, které teorii tvoří.
Ve fyzice je situace v určitém smyslu obtížnější, než v matematice. Když se vrátím k svému příkladu na začátku, v axiomech vektorového prostoru nad tělesem reálných čísel se předpokládá, že víme, co jsou reálná čísla. Reálná čísla se definují pomocí přirozených čísel a teorie přirozených čísel musí být opět vybudována axiomaticky. Můžeme však nejdříve vybudovat teorii reálných čísel a potom nad nimi budovat další struktury. Toto není možné v případě tak fundamentálních veličin fyzikálního popisu, jakými jsou prostor a čas.
Můžeme, a většinou to také děláme, si však vypomoci výše zmíněným "úkrokem". Na začátku předpokládáme, že existují ideální standardy určitých vlastností, ideální hodiny a ideální měřítka, s jejichž pomocí měříme časové a prostorové vztahy. Když máme formulovanou celou teorii, sestrojíme v jejím rámci modely těchto přístrojů. Podobně můžeme postupovat i u jiných veličin. (Zde mám na mysli klasické, tj. nekvantové teorie. Jak zkonstruovat v rámci kvantové teorie modely klasických přístrojů, které měří pozorovatelné veličiny, je jedním ze základních problémů interpretace kvantové mechaniky a nebudu se do něho pouštět. Tím ovšem nechci říci, že by ve standardní interpretaci kvantové teorie nebyly pojmy dobře definovány; prostě se předpokládá existence klasických přístrojů.)
V našem jednoduchém příkladu byla síla definována konkrétním předpisem, ve kterém vystupovaly jen předem nedefinované parametry qi, náboje jednotlivých hmotných bodů. Podívejme se, co by se stalo, pokud bychom na začátku neměli definiční formuli působících sil (2) a naši formulaci pohybového zákona bychom poněkud pozměnili:
Každému hmotnému bodu je přiřazena konstanta m, specifická pro daný bod, které říkáme hmotnost. Pohyb této soustavy hmotných bodů vzhledem k vztažnému systému, kterému říkáme inerciální, je pak určen vztahy
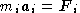 |
(1') |
veličiny Fi nazýváme síly.
Na první pohled je právě toto obecná formulace II. Newtonova zákona pro soustavu interagujících hmotných bodů, která zahrnuje i jiné síly než elektrostatické. Je samozřejmě v pořádku, pokud k ní přidáme definiční vztahy pro síly analogické rovnicím (2). Pokud ovšem o "silách" nic dalšího neřekneme, je informační obsah zákona nulový. Ať bude pohyb hmotných bodů jakýkoli, vždy najdeme takové funkce času Fi, pro které jsou vztahy splněny. I pokud předpokládáme, že náš systém hmotných bodů se chová tak, jak jsme předpokládali v našem elektrostatickém modelu, vztahy (1') nám implicite nedefinují inerciální systém a síly dané (2), protože v neinerciálním systému prostě přistoupí k elektrostatickým silám síly zdánlivé. Vztahy tedy budou platit v každém systému, jen předpis pro síly bude v inerciálních a neinerciálních systémech různý.
Takto formulovaný zákon je tedy experimentálně nevyvratitelný, či řečeno s K.Popperem [3], nefalsifikovatelný.
V učebnicích se ovšem II. Newtonův zákon často formuluje obdobným způsobem, ovšem s tím, že se pojem "pravé" síly doplňuje slovní formulací typu "síly mají původ v ostatních tělesech" či nějak podobně. Proti takové formulaci na určité úrovni nic nenamítám, je ale třeba nějak vyjasnit poněkud mlhavou specifikaci "síly mají původ...". Pro situaci, kterou teď máme na mysli to můžeme udělat třeba tak, že požadujeme, že veličiny Fi jsou funkcemi pouze rozdílů polohových vektorů jednotlivých hmotných bodů a parametrů charakteristických pro jednotlivé hmotné body (náboje, hmotnosti); nezávisí tedy explicite na čase. Tím vyloučíme zdánlivé síly a pohybový zákon opět implicite definuje inerciální systém. Pokud se "příroda" (rozuměj náš model) chová tak, že interakce, které působí, jsou dány pouze Coulombovým zákonem a newtonovským gravitačním zákonem, sledování pohybů hmotných bodů za různých počátečních podmínek nám dovolí určit správné vztahy pro síly. Podstatné zde je, že jsme omezili možné závislosti sil na proměnných vystupujících v našich vztazích. Tím, že předpokládáme explicitní nezávislost na čase např. víme, že když jednou necháme vyvíjet systém z určitých počátečních podmínek, tak při opakovaném experimentu se bude vyvíjet stejně. (Pokud hovoříme o konečné soustavě hmotných bodů, je formulace v pořádku i pro newtonovskou gravitaci. Pokud chceme rozšířit pohybový zákon na nekonečný, prakticky ale stačí dostatečně velký systém bodů, dostaneme se do potíží daných principem ekvivalence - proto je nekonsistentní newtonovská kosmologie. Tímto problémem se zde však nezabýváme.)
Obdobným způsobem můžeme rozšířit naše požadavky tak, aby zahrnovaly i obecnější síly (např. magnetické působení). Vždy ale musíme klást na síly určité požadavky. Takto se postupuje v axiomatických formulacích mechaniky, kterých během let vznikla značná řada. Potíž je v tom, že je obtížné položit dostatečně omezující a zároveň dostatečně obecné požadavky na síly, aby zahrnovaly všechny situace, ve kterých užíváme II. Newtonův zákon. (Vezmu-li např. jednoduchý příklad reálné pružiny, modelované harmonickým oscilátorem, jejíž elastické vlastnosti se mění v důsledku únavy materiálu, nemohu požadovat explicitní nezávislost na čase. Přesto ale budeme právě k určení této závislosti užívat II. zákona.) To co jsem zde chtěl říci shrnu následovně. Není problém axiomaticky vybudovat mechaniku, máme-li na mysli určitou hotovou teorii. Potíž je v tom, že chceme-li užívat mechaniku v běžné praxi, musíme mezi síly zahrnout i fenomenologické síly jako je elastické působení a v tom případě pracuje se stále nedokončenou teorií. Newtonův II. zákon tak má v některých případech charakter skutečného zákona (kdy předepíšeme konkrétní formule pro síly), v některých případech ho můžeme chápat jako implicitní definici sil (když jsme vhodně axiomaticky vymezili možné tvary sil) a v některých případech je spíše programovým schématem (když budujeme určitou fenomenologickou teorii).
Ve svém výkladu jsem zdůrazňoval, že vlastně jen mapuji nebo formalizuji to, co se skutečně ve fyzice dělá, proto nepředpokládám, že téma zaujme čistého badatele. Problém formální struktury fyziky nás začne více pálit v okamžiku, kdy fyziku vyučujeme a jsme nuceni veličiny nějak zavádět a problém je vlastně tím tíživější, čím na nižší úrovni fyziku vykládáme. Obraz fyziky jako sítě vztahů, které implicite definují jednotlivé pojmy je snad srozumitelný někomu, kdo už dost fyziky zná, pro začátečníka je však velice obtížně sdělný.
I když čtenář uzná oprávněnost mého rozboru pojmu síla v newtonovské teorii, je mu okamžitě jasné, že něco takového se nedá rozebírat v tom okamžiku, kdy se žák poprve setká s Newtonovými zákony.
Jak tedy základní veličiny zavádět? Je asi nezbytné se smířit s tím, že se v základním výkladu spokojíme s řadou nepřesných formulací, které se na vyšších úrovních precizují. Důležité asi není, aby žáci uměli věci správně definovat, ale aby se naučili s pojmy správně pracovat.
Na začátku jsem uváděl příklad, že výkladový slovník jazyka nám neposlouží, nemáme-li již před jeho čtením určitou slovní zásobu. To není tak docela pravda. Pokud někdo vůbec neumí česky, ale žije v prostředí podobnému našemu, může v principu jazyk dešifrovat tak, že bude postupně zkoušet dávat slovům různé významy a hledat, které kombinace dávají výroky s dobrým smyslem. Dobrým smyslem nyní rozumím to, že budou vypovídat správně o věcech, které student zná z reálné zkušenosti. Kontext určuje význam slov více méně jednoznačně, v tomto smyslu je jejich význam implicite definován sítí nejrůznějších výroků v daném jazyce vyslovených. Tak nějak se luští zaniklé jazyky, je to ovšem neobyčejně obtížný úkol.
Obdobně, i když podstatně schůdněji, se učíme mateřštinu. Pomocí ostentativních definic získáme představu o významu některých slov, která může být i mírně chybná. Postupně spojujeme výroky jako "máma jde" s určitou pozorovanou činností a časem začneme určitý základní slovník správně užívat. Když už jazykem vcelku dobře vládneme, osvojíme si postupně jeho gramatickou strukturu atd.
Vývoj učebnic za dobu, po kterou jej pozoruji, se vyznačuje snahou o přesnější definice pojmů a přesnější formulace základních fyzikálních zákonů. Je to jistě dobrá snaha, ale ne vždy je korunována dobrým výsledkem. Z mého článku mělo vyplynout, že jít cestou opravdu přesných deskriptivních definic z principiálních důvodů nejde.
Domnívám se, že je důležité, aby se nepředkládaly žákům výroky, které jsou vyloženě chybné. Na druhé straně by byl dostatečně dobrý výsledek, kdyby se žáci naučili správně řešit jednoduché úlohy, aniž by se kladl důraz na definice užívaných pojmů. Snaha o přesnější formulace často vede k výsledku, že formulace sice není stejně zcela přesná, zato je ale tak komplikovaná, že se stává nesrozumitelnou.
Nebudu uvádět konkrétní příklady z fyziky, protože bych se mohl některého autora dotknout. Ne že bych k tomu neměl v některých případech chuť, ale argumentace, proč určitou formulaci pokládám za nevhodnou, by musela být dosti rozsáhlá, protože by se musel podrobit kritice celý kontext příslušné knihy a to je téma na jiný, či více jiných článků.
Vrátím se proto opět k češtině. My jsme se ještě učili, že podstatná jména jsou jména osob, zvířat a věci. Tato definice je nesporně chybná, chápeme-li "podstatné jméno" jako definiendum a "jména osob, zvířat a věcí" jako definiens. Nicméně se s ní dobře pracovalo a snadno jsme z textu vybrali odpovídající substantiva. Bez velkých potíží potom žák později rozšířil pojem podstatného jména i na abstrakta.
Tento postup se mi zdá pedagogicky vhodný, protože podat vyčerpávající definici substantiva v podstatě nejde. (Podívejte se do encyklopedie na heslo podstatné jméno nebo do vysokoškolské učebnice jazyka a dáte mi za pravdu.) Jen bych volil, právě s ohledem na princip, že by se neměly říkat věci nesprávně, formulaci typu "Mezi podstatná jména řadíme jména osob,..." nebo "Podstatná jména jsou jména osob, zvířat a věcí a některá další slova". Nebylo by to na úkor srozumitelnosti a zvětšilo by to věcnou správnost.
Podobně ve fyzice bych se vyhýbal formulacím, které jsou nesprávné, není však nutné, aby se pojmy zaváděly v plné obecnosti. Je ale důležité, aby si učitel uvědomoval, že celá pojmová struktura se pomocí deskriptivních definic z logických důvodů vybudovat nedá a proto při zavádění pojmů pomocí definic zachovával určitou opatrnost.