Počítačové metody v teoretické fyzice II - NTMF058

Základní informace:

v roce 2024/2025 přednáší Karel Houfek
přednáška a cvičení se koná každý pátek od 10:40 v posluchárně ÚTF

Materiály ke stažení (zatím neúplné, budou postupně doplněny)

Poznámky a notebooky v Mathematice, které používám při přednáškách a cvičeních:

Iterační metody numerické lineární algebry
- doplňující materiál: vlastní čísla a vektory speciální tridiagonální matice (poznámky)
- stacionární iterační metody (poznámky)
- gradientní iterační metody (poznámky)
  - jednorozměrná Poissonova rovnice (notebook, pdf)
  - příklad z Trefethenovy učebnice (notebook, pdf)
- multigridová metoda (poznámky)
  - jednorozměrná Poissonova rovnice (notebook, pdf)
- Arnoldiho algoritmus a metoda GMRES (poznámky)
  - viz též konec notebooku obsahujícího příklad z Trefethenovy učebnice výše
- předpodmínění obecněji (poznámky)
- problém vlastních čísel a vektorů (zatím poznámky v angličtině)
  - basic methods - power, inverse, Rayleigh quotient, QR (notebook, pdf)
Numerické řešení PDR - metoda konečných diferencí
- úvod (poznámky)
- konvergence a stabilita (poznámky)
- doplnění a CFL podmínka (poznámky)
  - ukázka řešení u_t = u_x pomocí explicitních metod (notebook, pdf)
  - ukázka řešení u_t = u_xx + u_yy pomocí explicitních metod (notebook, pdf)
Numerické řešení PDR - metoda konečných prvků
- modelový problém (poznámky)
- kombinace s DVR bází vysokého řádu (poznámky)
  - řešení 1D Poissonova rovnice pomocí FEM-DVR (notebook, pdf)
  - řešení 1D časově závislé Schrödingerovy rovnice pro volnou částici pomocí FEM-DVR a Crankovy-Nicolsonové metody (notebook, pdf)
  - řešení 1D časově závislé Schrödingerovy rovnice pro volnou částici pomocí FEM-DVR a zobecněné Crankovy-Nicolsonové metody (notebook, pdf)
- obecný eliprický problém (poznámky)
- cvičení ve FreeFEM (poznámky)
  - řešení 2D Poissonovy rovnice pomocí FreeFEM (zip)
  - řešení 2D rovnice vedení tepla pomocí FreeFEM (zip)
  - řešení časově závislé 2D Schrödingerovy rovnice pro volnou částici pomocí FreeFEM (zip)
  - řešení časově závislé 2D Schrödingerovy rovnice pro částici v harmonickém oscilátoru pomocí FreeFEM (zip)
  - řešení časově závislé 2D Schrödingerovy rovnice pro rozptyl částice na potenciálu pomocí FreeFEM (zip)
Numerické řešení PDR - spektrální metody
- úvod - derivovací matice, modelový periodický problém (poznámky, aktualizováno 20.5., přidány 2 stránky na konec)
  - aproximace derivace pomocí derivovacích matic (notebook, pdf)
  - ilustrace přesnosti pro jednoduchou vlnovou rovnici (notebook, pdf)
  - odvození derivovacích matic pro periodický problém pomocí trigonometrické interpolace (notebook, pdf)
- spektrální metody přes Fourierovu transformaci (poznámky)
  - aproximace derivace pomocí FFT (notebook, pdf)
  - ilustrace řešení vlnové rovnice s proměnnou rychlostí - FFT (notebook, pdf)
  - ilustrace řešení vlnové rovnice s proměnnou rychlostí - spekrální derivovací matice (notebook, pdf)
  - ilustrace řešení vlnové rovnice s proměnnou rychlostí - konečné diference (pro srovnání přesnosti) (notebook, pdf)

Zadání zápočtových úloh

Podmínkou udělení zápočtu je vypracování zápočtové úlohy. Jak už jsem zmiňoval na přednášce, letošní úlohou je simulace dvouštěrbinového experimentu v kvantové mechanice, tedy řešení časově závislé dvourozměrné Schrödingerovy rovnice s počáteční podmínkou danou lokalizovaným Gaussovským balíkem, kterému udělíte počáteční hybnost např. ve směru osy x. V určité vhodné vzdálenosti od centra balíku ve směru pohybu umístěte bariéru kolmou na osu x (buď dostatečně vysokou, nebo na její hranici vynuťte nulovou okrajovou podmínku) se dvěma štěrbinami symetricky rozmístěnými od osy x. Pokud se podaří nasimulovat průchod vlnové funkce bariérou, je pak třeba pomocí integrace toku pravděpodobnosti v čase v určitém místě vyšetřit průběh pravděpodobnosti dopadu částice na detektor, který je umístěný kolmo osu x v určité vzdálenosti za bariérou, viz obrázek s možným počátečním nastavením. 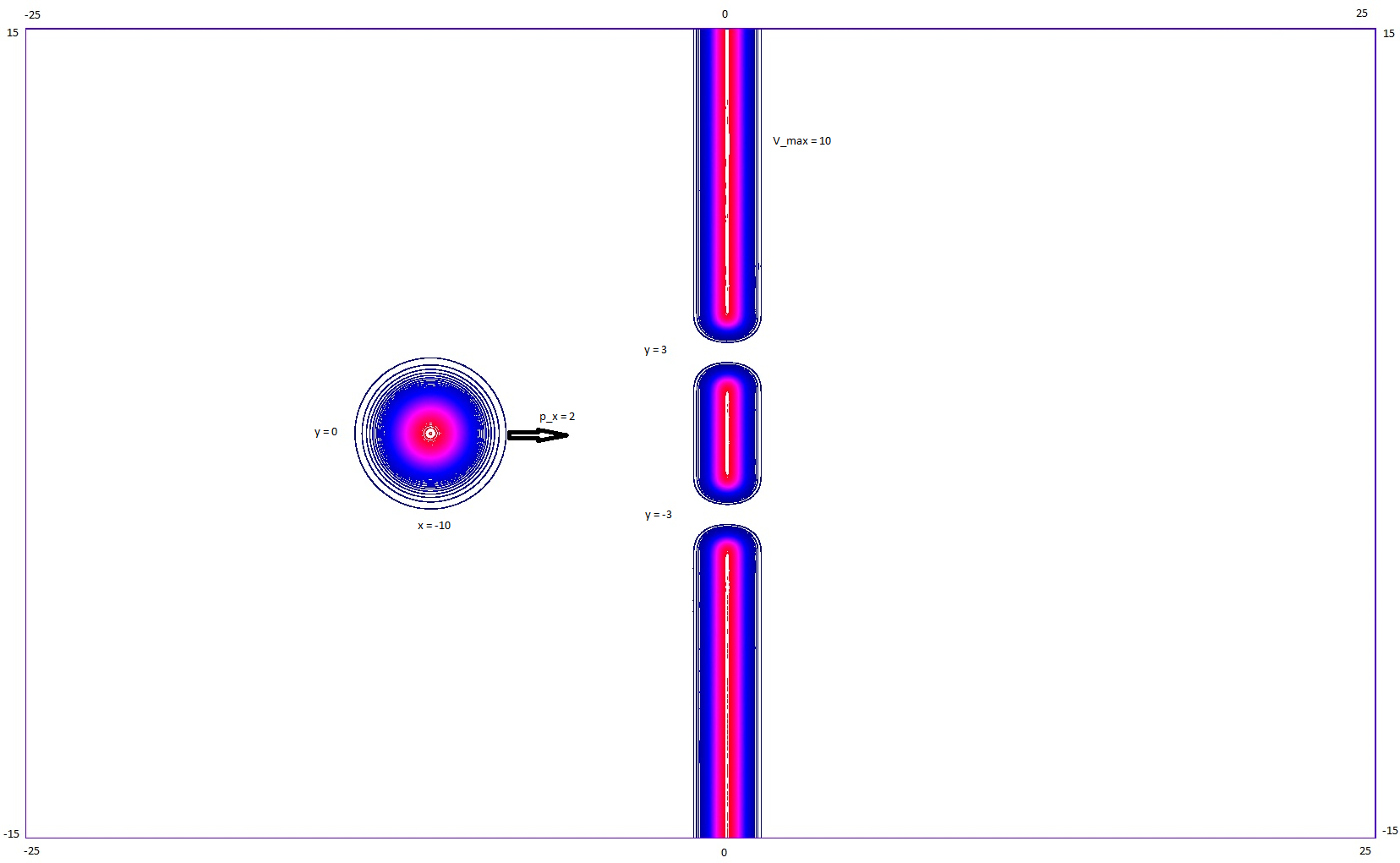posible initial setup
Pro simulaci použijete jednu z metod, které jsme na přednáškách probírali, případně jejich vhodnou modifikaci. Pokud jde o okrajové podmínky, je třeba si uvědomit, že nulová okrajová podmínka na hranici zvolené oblasti vede k odrazu vlnového balíku a je nutné se s tímto problémem nějak vypořádat. Buď musíte zvolit dostatečně velkou oblast, aby se vlnový balík nestihl odrazit, nebo můžete na hranici použít komplexní absorbční potenciál typu V_CAP = -i * c * (x - x_CAP), který je nenulový pro x větší než vhodně zvolené x_CAP a kde c je třeba nastavit tak, aby došlo k dostatečnému ultumení vlnového balíku před dosažením okraje zvolené oblasti. Při řešení pomocí metody konečných prvků můžete použít FreeFEM, případně jiný dostupný nástroj.

Také se male ůžeme domluvit, že místo zadané zápočtové úlohy vyřešíte nějaký problém související s Vaší diplomovou prací, ve které využijete některou z metod probíraných na přednášce. V tomto případě se domluvíme individuálně.

Požadavky ke zkoušce

Níže uvedená témata je potřeba znát v rozsahu přednášky, pokud např. nebyl na přednášce uveden důkaz některého tvrzení, pak nebude požadován ani u zkoušky. U jednotlivých hlavních témat je uvedena literatura, ze které jsem při přípravě přednášky především čerpal. Odkazy jsou na seznam doporučené literatury níže.

Iterační metody řešení soustav lineárních rovnic ([1 kap. 19, [3] kap. 6)
- základní iterační metody (Jacobiho, Gaussova-Seidelova, (super)relaxační metoda)
- gradientní iterační metody (metoda největšího spádu, metoda sdružených gradientů)
- mutligridová metoda, základní myšlenka a struktura, V-cyklus a full multigrid
Diferenční metody (metoda sítí) pro parciální diferenciální rovnice (PDR) ([1] kap. 17, 19 [2] kap. 3 a 4)
- základní explicitní a implicitní diferenční schémata pro počáteční úlohy (parabolické a hyperbolické PDR); metoda Eulerova, leap-frog, Laxova-Wendroffova, Crankova-Nicolsonova, jejich řád a stabilita; základní myšlenka metody přímek
- obecná formulace diferenčních schémat pro počáteční úlohy; lokální a globální přesnost (řád) metody; konvergence a stabilita, Laxova věta o ekvivalenci; Courantova-Friedrichsova-Lewyho podmínka; Fourierova analýza diferenčních schémat a von Neumannova podmínka stability
- základní použití diferenčních metod pro okrajové úlohy (eliptické PDR)
Základy metody konečných prvků pro okrajové úlohy ([4] kap. 1-3)
- variační a slabá formulace okrajové úlohy (pro eliptické PDR) a jejich ekvivalence
- řešení na konečných podprostorech (Ritzova variační metoda a Galerkinova metoda)
- podstata metody konečných prvků, lineární báze a základní odhad chyby
Spektrální metody ([5])
- úvod do spektrálních metod a jejich aplikace na řešení PDR
- souvislost spektrálních metod s Fourierovu transformací

Doporučená literatura

Níže uvedená literatura k přednášce je k dispozici ke stažení v "tajném" podadresáři, jehož jméno se dozvíte na přednášce či na požádání (nejlépe zasláním e-mailu přednášejícímu).

[1]	Press W. H., Teukolsky S. A., Vetterling W. T., Flannery B. P. - Numerical Recipes Third Edition - The Art of Scientific Computing, Third Edition, Cambridge University Press, Cambridge 2007, starší vydání dostupné online, především kapitoly 7 (metoda Monte-Carlo), 17(okrajové úlohy v 1D) a 19 (přehled metod pro PDR)
[2]	Trefethen L. N. - Finite Difference and Spectral Methods for Ordinary and Partial Differential Equations, 1996, dostupné online, především kapitoly 3 (diferenční metody) a 4 (stabilita a konvergence)
[3]	Demmel J. W. - Applied Numerical Linear Algebra, SIAM, Philadelphia 2007, především kapitola 6 (iterační metody)
[4]	Johnson C. - Numerical Solution of Partial Differential Equations by the Finite Element Method, Cambridge , New York 1987, především kapitoly 1-3 (metoda konečných prvků)
[5]	Trefethen L. N. - Spectral Methods in Matlab, SIAM, Philadelphia 2000, dostupné online
[6]	LeVeque R. J. - Finite Difference Methods for Ordinary and Partial Differential Equations, SIAM, Philadelphia 2007, především kapitoly 1, 3 (eliptické PDR), 4 (iterační metody), 9 (parabolické PDR) a 10 (hyperbolické PDR)
[7]	Vitásek E. - Numerické metody, SNTL, Praha 1987, především kapitoly I.2.2-I.2.3 (iterační metody), VI (eliptické PDR), VII (parabolické PDR) a VIII (hyperbolické PDR)
[8]	Isaacson E., Keller H. B. - Analysis of Numerical Methods, Dover, New York 1994, především kapitoly 2.4 (iterační metody), 9 (analýza metod pro PDR)

Numerické knihovny pro fyziku

Některé z níže zmíněných knihoven (jak ve FORTRANU, tak v jazyku C) a mnohé další pro řadu speciálních problémů lze najít na www.netlib.org.

1) CPC - Library, (hlavně FORTRAN)

Knihovna programů časopisu " Computer Physics Communications ", kde lze nalézt články popisující metody. Obsahuje řešení pro mnoho úloh s nimiž se setkáte ve fyzice, včetně pokročilých metod, npř. různé speciální funkce, řešení Hartree-Fockových rovnic, ...Dostupné v doméně fakulty.

2) GSL (Gnu scientific library) (orientovano na C, ale je zde i překladač a knihovny pro F90)

Široké spektrum matematických procedur různého zaměření, vše volně k dispozici.

3) BLAS, EISPACK, LINPACK, LAPACK (Primárně FORTRAN 77, FORTRAN 90, existuje C++ verze)

BLAS je základní balík pro manipulaci s vektory a maticemi (jeho náhrada, která se umí maximálně efektinvě přizpůsobit hardware (optimální využití cache paměti procesoru pro násobení matic atd.) se jmenuje ATLAS). Na něj staví EISPACK pro diagonalizaci matic a LINPACK pro lineární algebru. Jejich sloučením vznikl LAPACK, který obsahuje velké množství procedur pro numerickou lineární algebru.

4) Intel Fortran (C) MKL - library

Matematické knihovny dodávané k intelovským překladačům FORTRANU a C. Obsahují mimo jiné LAPACK a SPARSE SOLVER pro inverzi obecných řídkých matic.

5) NAG library

Komerční profesionální balík matematických knihoven.

6) Super LU - Berkeley

LU dekompozice pro obecné řídké matice.

7) Quadpack

Adaptibilní kvadratury .